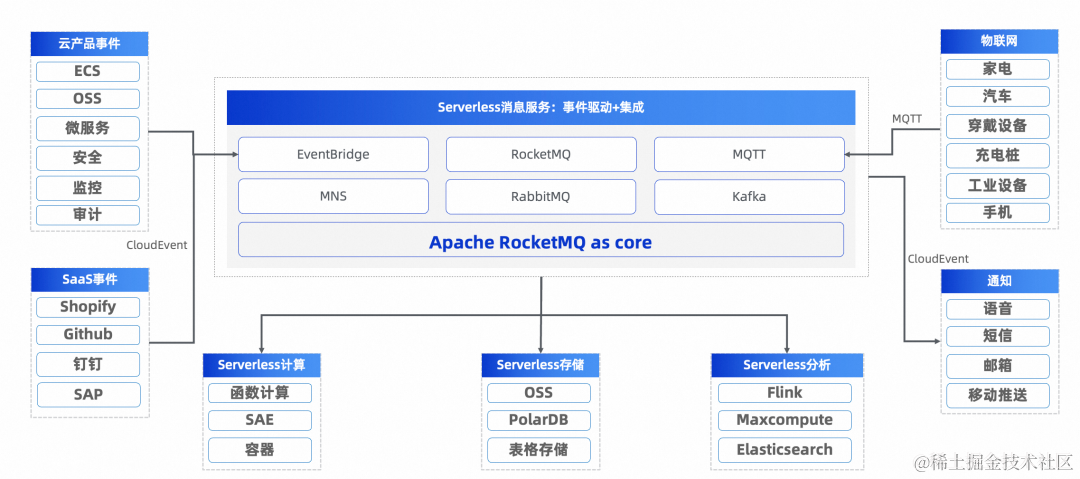
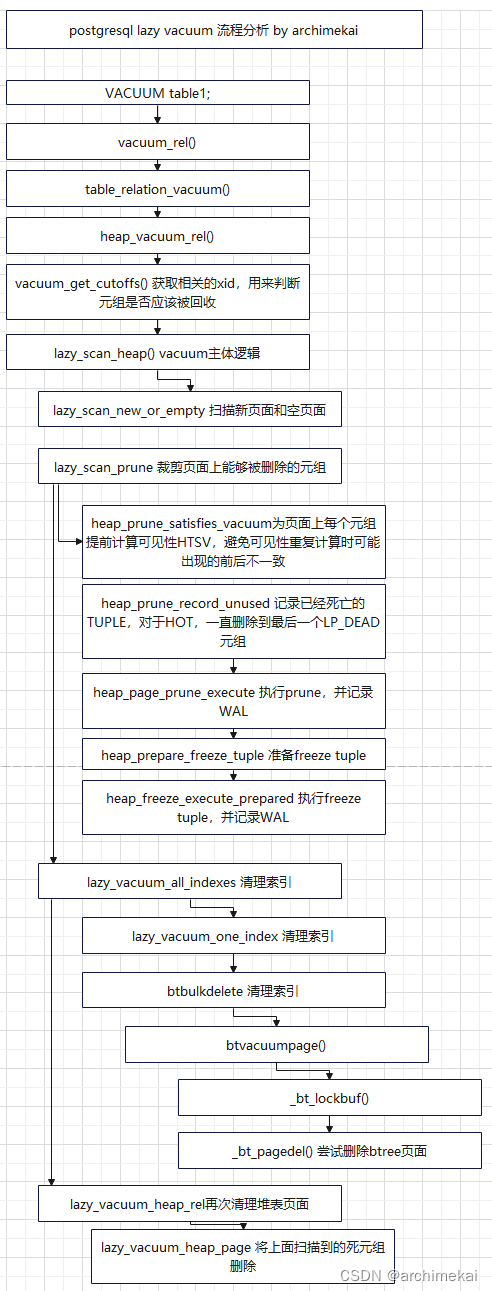
动态规划
动态规划就像是解决问题的一种策略,它可以帮助我们更高效地找到问题的解决方案。这个策略的核心思想就是将问题分解为一系列的小问题,并将每个小问题的解保存起来。这样,当我们需要解决原始问题的时候,我们就可以直接利用已经计算好的小问题的解,而不需要重复计算。
动态规划与数学归纳法思想上十分相似。
数学归纳法:
-
基础步骤(base case):首先证明命题在最小的基础情况下成立。通常这是一个较简单的情况,可以直接验证命题是否成立。
-
归纳步骤(inductive step):假设命题在某个情况下成立,然后证明在下一个情况下也成立。这个证明可以通过推理推断出结论或使用一些已知的规律来得到。
通过反复迭代归纳步骤,我们可以推导出命题在所有情况下成立的结论。
动态规划:
-
状态表示:
-
状态转移方程:
-
初始化:
-
填表顺序:
-
返回值:
数学归纳法的基础步骤相当于动态规划中初始化步骤。
数学归纳法的归纳步骤相当于动态规划中推导状态转移方程。
动态规划的思想和数学归纳法思想类似。
在动态规划中,首先得到状态在最小的基础情况下的值,然后通过状态转移方程,得到下一个状态的值,反复迭代,最终得到我们期望的状态下的值。
接下来我们通过三道例题,深入理解动态规划思想,以及实现动态规划的具体步骤。
174. 地下城游戏

题目解析

状态表示
我们可以定义,dp[i][j]表示从(i,j)位置出发,到达右下角所需的最小生命值。
状态的表示通常是经验+题目来得到的。
经验指的是,以某个位置为结尾,或者以某个位置开始。
这道题目我们选择以(i,j)位置开始到达最后的思路定义状态。
故状态表示为,dp[i][j]表示从(i,j)位置出发,到达右下角所需的最小生命值。
为什么选择这一种方式而不选择从(0,0)位置开始到达(i,j)位置所需的最小生命值?

上图所示,如果我们考虑蓝色和绿色两种路径,
绿色路径「从出发点到当前点的路径和」为 1,「从出发点到当前点所需的最小初始值」为 3。
蓝色路径「从出发点到当前点的路径和」为 −1,「从出发点到当前点所需的最小初始值」为 2。
我们希望「从出发点到当前点的路径和」尽可能大,而「从出发点到当前点所需的最小初始值」尽可能小。这两条路径各有优劣。
在上图中,我们知道应该选取绿色路径,因为蓝色路径的路径和太小,使得蓝色路径需要增大初始值到 4 才能走到终点,而绿色路径只要 3 点初始值就可以直接走到终点。但是如果把终点的 −2 换为 0,蓝色路径只需要初始值 2,绿色路径仍然需要初始值 3,最优决策就变成蓝色路径了。
因此,如果按照从左上往右下的顺序进行动态规划,我们无法直接确定到达 (1,2) 的方案,因为有两个重要程度相同的参数同时影响后续的决策。也就是说,这样的动态规划是不满足「无后效性」的。
于是我们考虑从右下往左上进行动态规划。令 dp[i][j] 表示从坐标 (i,j) 到终点所需的最小初始值。换句话说,当我们到达坐标 (i,j)时,如果此时我们的路径和不小于 dp[i][j],我们就能到达终点。
这是leetcode官方题解中的部分解析。
我们可以得出,如果用以某位置为结尾思路定义状态表示,我们没办法依靠前面的状态准确推导出(i,j)位置的状态,而后续的数据依旧会影响(i,j)位置的状态值,所以这种方式是错误的。在运用动态规划时,必须满足【无后效性】,所以我们选择以某位置开始思路定义状态表示。
当我们选择 以某位置开始思路定义状态表示时,我们前面的状态值并不会影响后面的状态值,可以保证满足【无后效性】,所以这种方式是可以行的。
故状态表示为,dp[i][j]表示从(i,j)位置出发,到达右下角所需的最小生命值。
状态转移方程
我们考虑,(i,j)位置的值能不能由其他的状态值推导得出,dp[i+1][j]表示从(i+1,j)位置出发,到达右下角所需的最小生命值。dp[i][j+1]表示从(i,j+1)位置出发,到达右下角所需的最小生命值。对于(i,j)的状态值,分两种情况,(i,j)房间内的值是正数或者是负数。如果(i,j)房间的值是负数,说明我们到达(i,j)时的最小生命值应该是min(dp[i][j+1],dp[i+1][j])-dungeon[i][j]。如果(i,j)房间的值是正数,说明我们到达(i,j)时的最小生命值应该是min(dp[i][j+1],dp[i+1][j])-dungeon[i][j],但是这样写又会有两种情况,那就是减出来的数是大于零的数或者是小于等于零的数,我们到达(i,j)房间时最小生命不可能是小于等于零的数,而减出来的数是小于等于零意义是,(i,j)的血包特别的大,即使你的血是负数,吃完之后都可以到达终点,所以实际上到达该位置的生命值为最低的1就可以。
故状态转移方程为,
dp[i][j]=min(dp[i+1][j],dp[i][j+1])-dungeon[i][j]
if(dp[i][j]<=0)dp[i][j]=1
初始化
根据状态转移方程,我们如果要推导出(i,j)位置的状态,就需要运用到(i+1,j)和(i,j+1)位置的状态,所以我们为了不越界,需要初始化最后一行和最后一列的数据。我们发现这种初始化有点复杂,所以我们把对这些位置的初始化转化为对虚拟节点的初始化,也就是创建虚拟节点代替原先初始化的位置。

对于红色位置的状态,他们所需访问的虚拟节点的值,是一定不能取到的,根据状态转移方程,
dp[i][j]=min(dp[i+1][j],dp[i][j+1])-dungeon[i][j]
if(dp[i][j]<=0)dp[i][j]=1
所以他们访问的虚拟节点值应该置正无穷,这样取最小就不会取到。
对于紫色位置的状态,他的状态值应该是1-dungeon[i][j]所以min(dp[i+1][j],dp[i][j+1])的值应该为1。所有我们可以先把所有位置置正无穷,然后在这两个位置选一个位置置1就可以了。

填表顺序
从右到左,从下到上
返回值
返回dp[0][0]
代码实现
int calculateMinimumHP(int** dungeon, int dungeonSize, int* dungeonColSize) {
int row=dungeonSize;
int col=dungeonColSize[0];
int dp[row+1][col+1];
for(int i=0;i<=row;i++){
memset(dp[i],0x3f,sizeof(dp[i]));
}
dp[row-1][col]=1;
for(int i=row-1;i>=0;i--){
for(int j=col-1;j>=0;j--){
dp[i][j]=fmin(dp[i][j+1],dp[i+1][j])-dungeon[i][j];
if(dp[i][j]<=0) dp[i][j]=1;
}
}
return dp[0][0];
} for(int i=0;i<=row;i++){
memset(dp[i],0x3f,sizeof(dp[i]));
}void *memset(void *s, int ch, size_t n);
函数解释:将s中前n个字节 (typedef unsigned int size_t )用 ch 替换并返回 s 。
memset:作用是在一段内存块中填充某个给定的值,它是对较大的结构体或数组进行清零操作的一种最快方法。

![]()
_itoa可以把x值转化为char类型的2进制数存放在string中。
我们发现x的二进制数是00111111 00111111 00111111 00111111。
用_itoa转换二进制数时,前导零省略了,实际上是00111111 00111111 00111111 00111111。
一个int类型占4个字节。
一个字节占8位二进制数。
而0x3f的二进制数是00111111。
memset的意思是,将x中前n个字节,用0x3f最后一个字节对应的二进制数替换。
那为什么要赋值0x3f:
作为无穷大使用
因为4个字节均为0x3f时,0x3f3f3f3f的十进制是1061109567,也就是10^ 9级别的(和0x7fffffff一个数量级),而一般场合下的数据都是小于10^9的,所以它可以作为无穷大使用而不致出现数据大于无穷大的情形。
可以保证无穷大加无穷大仍然不会超限。
另一方面,由于一般的数据都不会大于10^9,所以当我们把无穷大加上一个数据时,它并不会溢出(这就满足了“无穷大加一个有穷的数依然是无穷大”),事实上0x3f3f3f3f+0x3f3f3f3f=2122219134,这非常大但却没有超过32-bit int的表示范围,所以0x3f3f3f3f还满足了我们“无穷大加无穷大还是无穷大”的需求。
面试题 17.16. 按摩师
题目解析

状态表示
我们可以定义dp[i]表示,从nums[0]开始一直到nums[i],选择不相邻的预约情况中,最长的时间数。
状态转移方程
我们想一想dp[i]能不能由其他的状态推导得出。
dp[i]表示,从nums[0]开始一直到nums[i],选择不相邻的预约情况中,最长的时间数。
dp[i-1]表示,从nums[0]开始一直到nums[i-1],选择不相邻的预约情况中,最长的时间数。
dp[i-2]表示,从nums[0]开始一直到nums[i-2],选择不相邻的预约情况中,最长的时间数。
如果i位置预约我们选择,那么i-1位置预约肯定不选择,这种情况对应的最长时间数就是
dp[i-2]+nums[i]
如果i位置预约我们不选择,这种情况对应的最长时间数就是
dp[i-1]
因为我们存储是最长时间数,所以需要从两种情况中选一个时间更长的。
故状态转移方程为,dp[i]=max(dp[i-2]+nums[i],dp[i-1])
初始化
根据状态转移方程,我们推导出i位置的状态需要用到(i-2)和(i-1)的状态值。
我们想要统一所有需要得到的状态,都通过状态转移方程推导得出,那么我们就需要创建虚拟节点替代需要初始化的位置。
创建虚拟节点有几点注意事项,
第一,对虚拟节点的初始化必须保证后续的推导过程不出错。
第二,注意下标映射关系的变化,也就是状态表示和状态转移方程的下标变换。

状态转移方程为,dp[i]=max(dp[i-2]+nums[i-2],dp[i-1])。
对于紫色第一个状态值,应该是填自己的时间数,所以需要选择dp[i-2]+nums[i-2]且dp[n-2]需要为零,即dp[0]为0。
对于紫色第二个状态值,要么是填自己的值,要么填紫色第一个状态值。
所以dp[i-2]为零,即dp[1]。
故初始化为dp[0]=dp[1]=0。
填表顺序
从左往右
返回值
放回最后一个元素的值,dp[n+1]
n是nums的数组大小
代码实现
int massage(int* nums, int numsSize){
int n=numsSize;
int dp[n+2];
memset(dp,0,sizeof(dp));
for(int i=2;i<=n+1;i++){
dp[i]=fmax(dp[i-2]+nums[i-2],dp[i-1]);
}
return dp[n+1];
}
213. 打家劫舍 II

题目解析


我们可以把问题分成两种情况,要么数组的长度大于1,要么数组的长度等于1。
当数组的长度大于1时,我们有两种情况。
第一,我们考虑第一个房子,不考虑最后一个房子。
第二,我们不考虑第一个房子,考虑最后一个房子。
这样问题就转化为普通的不环绕的问题了。
当数组的长度等于1时,我们只能选择nums[0],这一个房子。
所以我们只需要解决不环绕的问题即可。
状态表示
我们可以定义dp[i]表示从nums[0]开始到nums[i]这些房子,选择不相邻房子方法数中金额最大的金额数。
状态转移方程
我们想一想dp[i]能不能由其他状态推导得出。
dp[i]表示从nums[0]开始到nums[i]这些房子,选择不相邻房子方法数中金额最大的金额数。
dp[i-1]表示从nums[0]开始到nums[i-1]这些房子,选择不相邻房子方法数中金额最大的金额数。
dp[i-2]表示从nums[0]开始到nums[i-2]这些房子,选择不相邻房子方法数中金额最大的金额数。
对dp[i]这个状态进行分析,如果该房子选择的话,i-1房子就不能选择,所以这种情况下金额最大数为dp[i-2]+nums[i]
如果该房子不选择的话,最大金额数就是dp[i-1]
故状态转移方程为,dp[i]=max(dp[i-2]+nums[i],dp[i-1])
初始化
根据状态转移方程,我们推导出i位置的状态需要用到(i-2)和(i-1)的状态值。
我们想要统一所有需要得到的状态,都通过状态转移方程推导得出,那么我们就需要创建虚拟节点替代需要初始化的位置。
创建虚拟节点有几点注意事项,
第一,对虚拟节点的初始化必须保证后续的推导过程不出错。
第二,注意下标映射关系的变化,也就是状态表示和状态转移方程的下标变换。

状态转移方程为,dp[i]=max(dp[i-2]+nums[i-2],dp[i-1])。
对于紫色第一个状态值,应该是填自己的时间数,所以需要选择dp[i-2]+nums[i-2]且dp[n-2]需要为零,即dp[0]为0。
对于紫色第二个状态值,要么是填自己的值,要么填紫色第一个状态值。
所以dp[i-2]为零,即dp[1]。
故初始化为dp[0]=dp[1]=0。
填表顺序
从左往右
返回值
分两种情况,计算当长度大于1时,考虑第一个房子而不考虑最后一个房子的金额数,
和当长度大于1时,不考虑第一个房子而考虑最后一个房子的金额数。
和当长度为1时,nums[0]的金额数
返回三者中最大的金额数即可。
代码实现
int rob_(int* nums,int numsSize, int left,int right) {
int n=numsSize;
int dp[n+2];
memset(dp,0,sizeof(dp));
for(int i=left;i<=right;i++){
dp[i]=fmax(dp[i-2]+nums[i-2],dp[i-1]);
}
return dp[right];
}
int rob(int* nums,int numsSize){
int num1=rob_(nums,numsSize,2,numsSize);
int num2=rob_(nums,numsSize,3,numsSize+1);
return fmax(fmax(num1,num2),nums[0]);
}我们rob_函数就是解决不环绕的一列房子问题。
接着把环绕的问题转化为不环绕的问题。
如果数组的长度大于1。
如果我们考虑第一个房子,而不考虑最后一个房子,只需要填写dp表中下标2到下标numsSize状态的推导填写。
如果我们不考虑第一个房子,而考虑最后一个房子,只需要填写dp表中下标3到下标numsSize+1的状态的推导填写。
如果数组的长度等于1。
考虑nums[0]的金额数。
如果数组长度为1,num1和num2计算出来的值都是零,因为numsSize 为1,而循环是从下标2开始或者从下标3开始,所以最后的返回值是初始化的零。
此时只需要返回nums[0]即可,nums [0]一定大于0。
所以返回比较num1,num2和nums[0]即可。
结尾
今天我们学习了动态规划的思想,动态规划思想和数学归纳法思想有一些类似,动态规划在模拟数学归纳法的过程,已知一个最简单的基础解,通过得到前项与后项的推导关系,由这个最简单的基础解,我们可以一步一步推导出我们希望得到的那个解,把我们得到的解依次存放在dp数组中,dp数组中对应的状态,就像是数列里面的每一项。最后感谢您阅读我的文章,对于动态规划系列,我会一直更新,如果您觉得内容有帮助,可以点赞加关注,以快速阅读最新文章。
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!









![[python]用python实现对arxml文件的操作](https://img-blog.csdnimg.cn/7ddd480aac8447b59c56eb11fe4c0067.png)