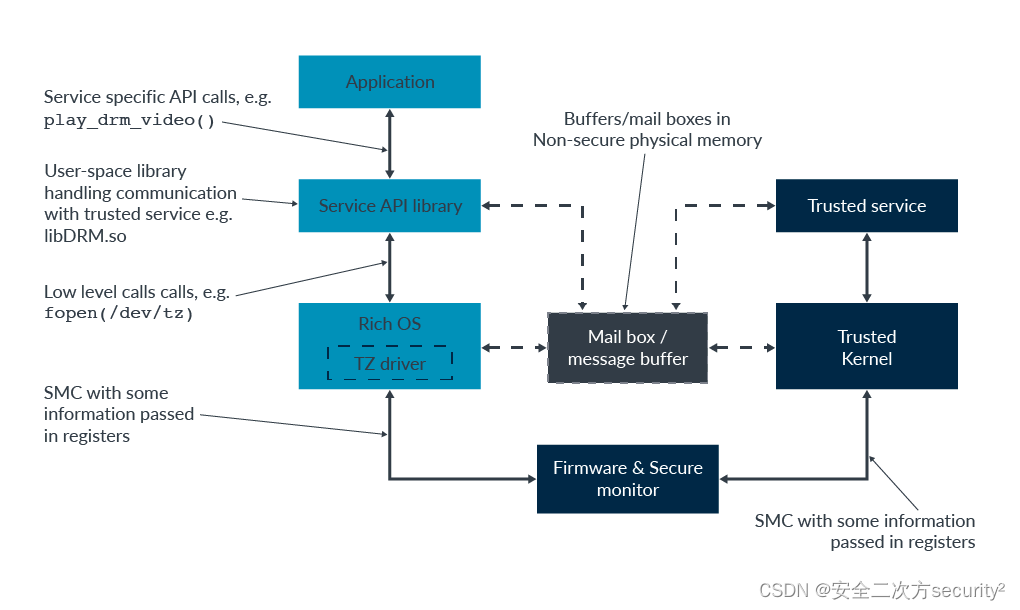
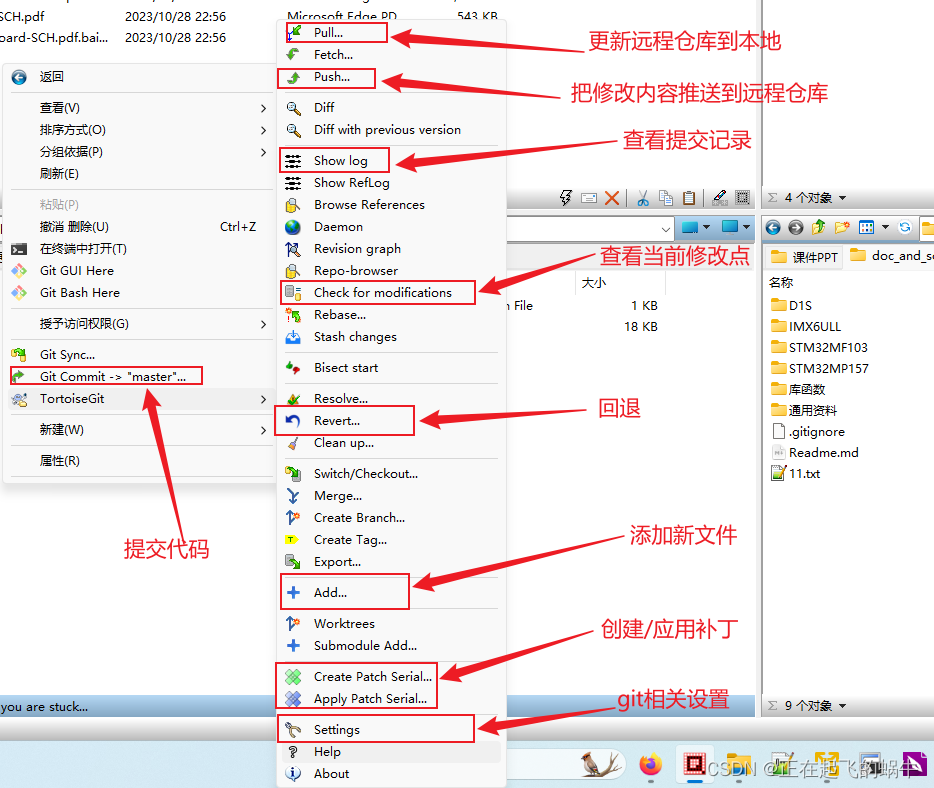
目录

原题描述：

时间：1s 空间：256M

题目描述：

输入格式：

输出格式：

样例1输入：

题目大意：

主要思路：

注意事项：

总代码：

---

原题描述：

时间：1s 空间：256M

题目描述：

小信家里有段木材，初始长度表示为数组。他可以进行以下填补操作至多次（可以不操作）：

选择两段木材，将长度截补到上，即操作后,。

填补操作后，小信要将木材都砍成相同长度的小段，并且不能有剩余，请你告诉他最长的小段能有多长？

输入格式：

第一行包含两个整数表示木材数和操作数。

第二行包含个整数，表示每段木材的初始长度。

输出格式：

输出一个整数，表示最长的小段的长度。

样例1输入：

2 1

15 9

样例1输出：

8 

样例2输入：

2 10

15 9 

样例2输出：

24 

约定与提示：

对于100%的数据，。

样例1解释：选择操作之后序列变成，能切成根长度为的木材。

样例2解释：选择 操作次之后序列变成，能切成根长度为  的木材。

题目大意：

就是给你一个数组，然你可以操作最多m次，每次操作可以将一个数-1，另一个数+1，最后问你所有数的最大共约数（就是gcd)

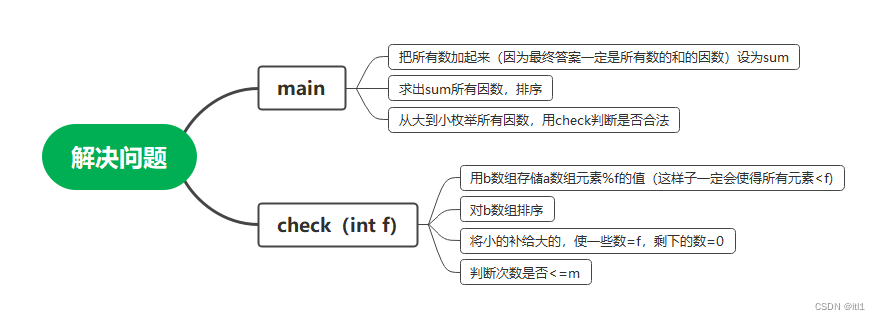
主要思路：

直接上思维导图：

说一下几个重点，给上代码片段：

1. 求因数：

   int cnt=0;//数组下标 
   for(int i=1;i*i<=sum;i++)//只要枚举到（sqrt(sum）就可以了 
   {
   	if(sum%i == 0)//如果是因数 
   	{
   		factor[cnt++] = i;//用来记录因数，放入因数数组中 
    		if(i*i!=sum)//如果不是sum的平方根 
   	    {
   			factor[cnt++] = sum/i;//sum/i也是sum的因数 
   		}
   	}
   }

2. 将小的补给大的：

   int t=0;//记录花费次数 
   int pos=1;//记录从哪个小的开始补（就是被减的） 
   for(int i=n;i>=1;i--)//枚举大的 
   {
   	if(b[i]!=0)//如果不是大的（也可以这么理解（被用光了） 
   	{
   	    int x=f-b[i];//记录要消耗的次数（也是要被补多少） 
   	    t+=x;//计入次数 
   	    while(x>0)//如果还需要补 
   	    {
   		    if(b[pos]>=x)//如果小的可以补完 
   	        {
   			    b[pos]-=x;//就补了 
   			    break;//跳出 
   	    	}
   		    else
   		    {
   			    x-=b[pos];//否则就消耗一些要补的 
       			b[pos] = 0;//把小的设成0
   	    		pos++;//就让下一个小的来补 
   		    }
   	    }
       }
   }
   /*
   直接看不太好看，我演示一遍。
   
   当f = 8,b数组为：{1,2,5}，pos=1; 
   先枚举到5。t+=3, x=3。
   开始补
   第一次发现不可以全补完。
   b[pos]也就是b[1]<3,那就耗掉一些。b[1] = 0,x=2,pos=2。 
   第二次发现可以补完，那就补完，b[2]-=2就是0，跳出。
   此时的b数组为：{0,0,5}
   i枚举到 2时，b[2] == 0了，也就是被用光了，那就跳过。 
   i枚举到 1时，b[1] == 0了，也就是被用光了，那就跳过。
   现在应该理解了吧。 
   */ 

注意事项：

不要把check中的b写成a了哦。

第一个合法因数输出后要return 0;

总代码：

#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[510];
int b[510];
int sum; 
int factor[10010];//用来记录因数 
bool check(int f)
{
    //千万不要把b写成a
	for(int i=1;i<=n;i++)
	{
		b[i] = a[i]%f;
	}
	sort(b+1,b+1+n);
	int t=0;//记录花费次数 
	int pos=1;//记录从哪个小的开始补（就是被减的） 
	for(int i=n;i>=1;i--)//枚举大的 
	{
		if(b[i]!=0)//如果不是大的（也可以这么理解（被用光了） 
		{
			int x=f-b[i];//记录要消耗的次数（也是要被补多少） 
			t+=x;//计入次数 
			while(x>0)//如果还需要补 
			{
				if(b[pos]>=x)//如果小的可以补完 
				{
					b[pos]-=x;//就补了 
					break;//跳出 
				}
				else
				{
					x-=b[pos];//否则就消耗一些要补的 
					b[pos] = 0;//把小的设成0
					pos++;//就让下一个小的来补 
				}
			}
		}
	}
	/*
	直接看不太好看，我演示一遍。
	
	当f = 8,b数组为：{1,2,5}，pos=1; 
	先枚举到5。t+=3, x=3。
	开始补
	第一次发现不可以全补完。
	b[pos]也就是b[1]<3,那就耗掉一些。b[1] = 0,x=2,pos=2。 
	第二次发现可以补完，那就补完，b[2]-=2就是0，跳出。
	此时的b数组为：{0,0,5}
	i枚举到 2时，b[2] == 0了，也就是被用光了，那就跳过。 
	i枚举到 1时，b[1] == 0了，也就是被用光了，那就跳过。
	现在应该理解了吧。 
	*/ 
	return t<=m;
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		sum+=a[i];
	}
	int cnt=0;//数组下标 
	for(int i=1;i*i<=sum;i++)//只要枚举到（sqrt(sum）就可以了 
	{
		if(sum%i == 0)//如果是因数 
		{
			factor[cnt++] = i;//放入因数数组中 
			if(i*i!=sum)//如果不是sum的平方根 
			{
				factor[cnt++] = sum/i;//sum/i也是sum的因数 
			}
		}
	}
	sort(factor,factor+cnt);
	for(int i=cnt-1;i>=0;i--)//从大到小枚举，这样子第一个合法因数一定是最大的
	{
		if(check(factor[i]))//用来判断每个因数是否合法
		{
			cout<<factor[i];
			return 0;//别忘了return 0;
		}
	}
	return 0;
}