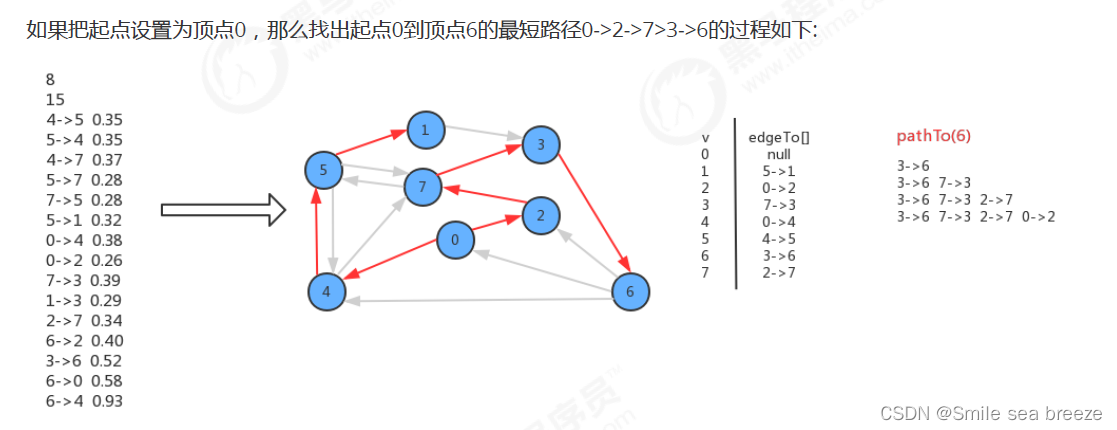
二刷复习
文章目录
- 二刷复习
- 哈希表和哈希法
- unordered 和 ordered 的不同
- 242.有效字母的异位词
- 349.两个数组的交集
- 202.快乐数
- 两数之和
- 四数相加2
- 383.赎金信
- 三数之和(这道题需要重复做, 双指针)
- 四数之和
哈希表和哈希法
哈希表:这是两种不一样的东西,首先哈希表是一种底层的数据结构
散列:其次,哈希法也叫散列法,是一种映射,key value的映射
python中如果想使用散列法可以使用set或者dict, set只储存键不储存值,dict可以储存键值对。
两者的底层实现都是哈希表,应该是相当于unordered_set和unordered_map; 所以dict可以在常数级别的增 删 查
哈希法,当我们遇到了要快速判断一个元素是否出现集合里的时候 或者 需要判断一个元素是否出现过,就要考虑哈希法。
unordered 和 ordered 的不同
首先无序和有序是针对key值的
(无序)unordered_set, map 底层是哈希表 所以查询 增删效率都是O(1)
(有序)ordered_set的话, c++std库中分为std::set和std::multiset; 我们知道set储存key值,ordered_set底层是用红黑树去储存key值的,这是一种平衡二叉树,所以key值是有序的,但key不可以修改,改动key值会导致整棵树的错乱,所以只能删除和增加。
set只能增删
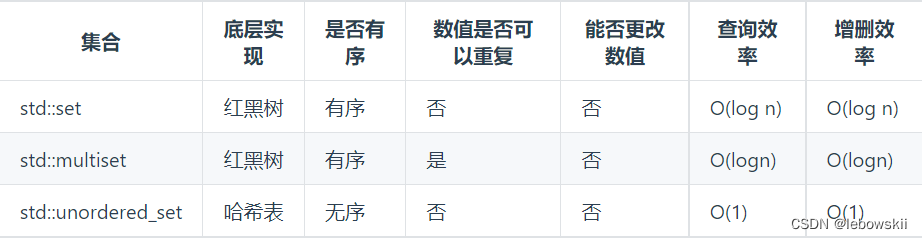
ordered_map, map中key不能修改,value可以修改, 有序map的话 key是用红黑树储存的
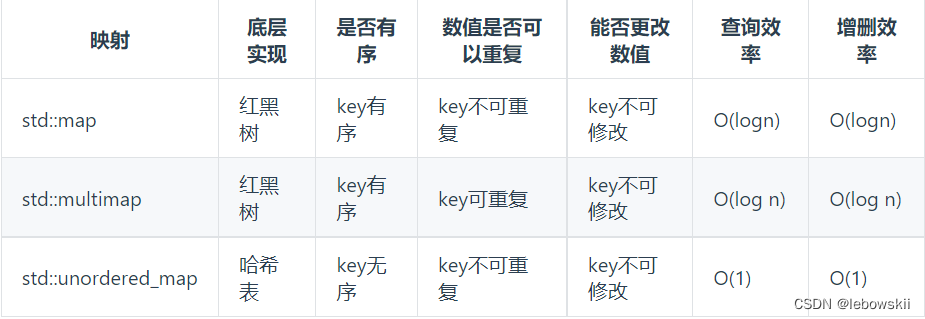
242.有效字母的异位词
有效字母异位词
from collections import Counter
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
a, b = Counter(s), Counter(t)
return a == b
349.两个数组的交集
两个数组的交集
交集用 & , 并起来用 |
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
return list(set(nums1) & set(nums2))
202.快乐数
快乐数
为什么这道题在哈希表这节里,因为在这个循环中可能有一个数反复出现,颠来倒去还是那个就会死循环; 这个时候就可以考虑用哈希了,每次我们把结果加进集合里,如果发现出现在集合里了我们return False; 出现1了我们return True
数位运算
while n:
x = n % 10
对x操作
n = n // 10
def isHappy(self, n: int) -> bool:
def cal(num: int) -> int:
sum_ = 0
while num:
sum_ += (num % 10) ** 2
num = num // 10
return sum_
record = set()
while True:
sum = cal(n)
if sum == 1: return True
if sum in record: return False
else: record.add(sum)
n = sum
两数之和
两数之和
哈希表储存的是 数组下标, 由于我们遍历的时候可以知道其中一个下标了,可以直接return [i, a[tar-nums[i]]]
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
a = dict()
for i in range(len(nums)):
if target-nums[i] in a: return [i, a[target-nums[i]]]
else: a[nums[i]] = i
四数相加2
四数相加2
这道题的关键在于,四个数组是分离的,可以单独从中选的,你选12 一组 34一组 和 13一组24一组是等价的;思路就在于分组做哈希
class Solution:
def fourSumCount(self, nums1: List[int], nums2: List[int], nums3: List[int], nums4: List[int]) -> int:
hashtable = dict()
for a in nums1:
for b in nums2:
if a+b not in hashtable: hashtable[a+b] = 1
else: hashtable[a+b] += 1
cnt = 0
for c in nums3:
for d in nums4:
if -(c+d) in hashtable: cnt += hashtable[-c-d]
return cnt
383.赎金信
383赎金信
思路: 就是看第二个字符串是否能完全提供给第一个字符串,首先是第一个字符串有的元素第二个字符串都得有,其次对应的value要足够
class Solution:
def canConstruct(self, ransomNote: str, magazine: str) -> bool:
r, m = Counter(ransomNote), Counter(magazine)
for key in r.keys():
if key not in m.keys(): return False
else:
if r[key] <= m[key]: continue
else: return False
return True
三数之和(这道题需要重复做, 双指针)
三数之和
一个是双指针逻辑,一个是去重逻辑;去重放在哪;先放进去一组之后再去重;
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
n = len(nums)
if n < 3: return []
res = []
nums.sort()
for i in range(n):
if nums[i] > 0: break
if i > 0 and nums[i] == nums[i-1]: continue
l, r = i+1, n-1
while l < r:
if nums[i] + nums[l] + nums[r] == 0:
res.append([nums[i], nums[l], nums[r]])
while l < r and nums[l] == nums[l+1]: l += 1
while l < r and nums[r] == nums[r-1]: r -= 1
l += 1
r -= 1
elif nums[i] + nums[l] + nums[r] < 0: l += 1
else: r -= 1
return res
四数之和
四数之和
和上面三数之和逻辑一样,都是双指针放缩;只是在双指针前增加了一层
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
n = len(nums)
if n < 4: return []
res = []
nums.sort()
for i in range(n):
if i > 0 and nums[i] == nums[i-1]: continue
for j in range(i+1,n):
if j > i+1 and nums[j] == nums[j-1]: continue
p = j + 1
q = n-1
while p < q:
if nums[i] + nums[j] + nums[p] + nums[q] > target: q -= 1
elif nums[i] + nums[j] + nums[p] + nums[q] < target: p += 1
else:
res.append([nums[i], nums[j], nums[p], nums[q]])
while p < q and nums[p] == nums[p + 1]: p += 1
while p < q and nums[q] == nums[q - 1]: q -= 1
p += 1
q -= 1
return res