论文地址：https://openaccess.thecvf.com/content/ICCV2023/html/Tian_DPS-Net_Deep_Polarimetric_Stereo_Depth_Estimation_ICCV_2023_paper.html

---

概述

  立体匹配模型难以处理无纹理场景的匹配，现有的方法通常假设物体表面是光滑的，或者光照是受控的，这些条件在实际场景中很难满足，只适用于物体级别的重建或者特定的拍摄环境。此外，这些方法还难以处理偏振图像中表面法向的固有歧义性，例如方位角和天顶角的歧义性（指从偏振图像中恢复表面法向量时，由于不同的反射类型和非线性方程的影响，可能存在多个解，导致法向量的方位角和天顶角不唯一），这些歧义性需要依赖于预先计算的粗糙深度或者已知的反射类型来解决。
  针对这些问题，文中提出DPS-Net来基于先验几何知识与偏振立体知识用于估计两幅偏振立体图像的深度。通过构建RGB与偏振匹配代价体分别提取RGB与偏振域的匹配知识。针对立体匹配中的固有歧义问题，文中引入一种等深度代价体用于解决无纹理区域的匹配模糊性，该代价体是一种利用偏振信息和几何约束来消除方位角歧义的方法，它基于等深度轮廓与法向量方位角分量正交的性质，通过计算偏振图像中的偏振角和方位角之间的差异，构建一个统一的代价函数，同时考虑了漫反射和镜面反射的情况。此外，文中提出一种级联双GRU结构将极化的等深度约束和多域的视觉相似度融合起来，通过递归地回归和优化视差，处理了极化信息中固有的方位角和天顶角的歧义，用于迭代更新视差图与有效地融合多源的关联特征与等深度代价。在合成和真实数据集中的实验结果表明，该方法达到了SOTA水准。

---

背景知识

  偏振光图像是指用不同的偏振角度拍摄的一组图像，它们可以反映物体表面的法向信息，有助于纹理缺乏的场景的匹配。偏振光是指光波的振动方向只沿着一个平面的光，它可以通过一个偏振片来产生或筛选，偏振片是一种只允许特定方向的偏振光通过的光学器件，它可以通过旋转来改变偏振角度。光波是一种横波，即光波的振动方向和传播方向垂直。根据横波的性质，不同偏振角度的偏振光图像的亮度会有不同的变化，这种变化与物体表面的法向量有关。偏振光图像的亮度和偏振角之间的关系可以用一个余弦函数来表示:
$$\begin{array}{rl}I\left({\varphi }_c\right)& =I_{\max }{\cos }^2\left({\varphi }_c-\varphi \right)+I_{\min }{\sin }^2\left({\varphi }_c-\varphi \right),\\ & =\bar{I}+\rho \bar{I}\cos \left(2{\varphi }_c-2\varphi \right),\end{array}\text{\hspace{1em}(1)}$$
其中${\varphi }_c$是偏振角，$\varphi$是物体表面的偏振角，$\rho$是物体表面的偏振度，$I$是物体表面的亮度，$I_{min},I_{max},\bar{I}=（I_{min}+I_{max}）/2$ 为物体表面的最小亮度，最高亮度与平均亮度。最大亮度和最小亮度是指在不同的偏振角度下，偏振光图像的亮度的最大值和最小值。平均亮度是指最大亮度和最小亮度的平均值，反映了物体表面的总体亮度。偏振角是指使偏振光图像达到最大亮度的偏振角度，它与物体表面的法向量有关，可以用于计算物体表面的法向角。偏振度是指最大亮度和最小亮度之间的相对差异，它反映了物体表面的偏振特性，可以用于判断物体表面的反射类型。这个方程可以用于从偏振光图像中计算出物体表面的偏振角和偏振度，进而推导出物体表面的法向量.
  当光线从空气射到物体表面时，会发生反射和折射，反射光会部分地偏振，即光波的振动方向只沿着一个平面。反射光的偏振程度和方向取决于物体表面的法向量和反射类型。反射类型分为漫反射和镜面反射，漫反射是指光线在物体表面的微小凹凸处发生多次反射，镜面反射是指光线在物体表面的平滑处发生一次反射。一般情况下，每个像素处的反射类型是由物体表面的材质和光照条件决定的。偏振度$\rho$，偏振角$\varphi$，天顶角$\theta$和方位角$\phi$是描述偏振光图像的几个重要参数。偏振度是指反射光的偏振程度，偏振角是指反射光的偏振方向，天顶角是指物体表面的法向量与视线方向的夹角，方位角是指物体表面的法向量在水平面上的投影与水平基准方向的夹角。根据物理原理，偏振度，偏振角，天顶角和方位角之间存在一定的关系，这些关系可以用数学方程来表示:
$$\begin{array}{c}{\rho }_d=\frac{(\eta -1/\eta {)}^2{\sin }^2\theta }{\begin{array}{r}2+2{\eta }^2-(\eta +1/\eta {)}^2{\sin }^2\theta +4\cos \theta \sqrt{{\eta }^2-{\sin }^2\theta }\\ {\varphi }_d=\phi \mathrm{or}{\varphi }_d=\phi +\pi ,\end{array}},\end{array}\text{\hspace{1em}(2)}$$
其中 $\eta$ 为表面材料的折射率，对镜面反射，有：
$$\begin{array}{c}{\rho }_s=\frac{2{\sin }^2\theta \cos \theta \sqrt{{\eta }^2-{\sin }^2\theta }}{{\eta }^2-{\sin }^2\theta -{\eta }^2{\sin }^2\theta +2{\sin }^4\theta },\\ {\varphi }_s=\phi \pm \frac{\pi }{2}.\end{array}\text{\hspace{1em}(3)}$$
通过求解上述方程中的方位角和天顶角，可以估算出表面法线，而由于未知的反射类型和非线性方程，方位角和天顶角都存在多解，这也被称为方位角模糊性和天顶角模糊性。

模型架构

  如图1所示，整体模型可以划分为4个步骤：（1）分别从RGB与偏振立体图像提取特征。（2）分别使用RGB与偏振立体特征构建匹配代价体。（3）根据偏振信息约束计算等深。（4）将相关性代价体与等深代价送入GRU单元中不断迭代更新视差图。

Multi Domain Feature and Correlation Volume 多源特征与相关性代价体

特征提取：分别使用特征提取模块从RGB立体图像与偏振立体图像中提取维度为256的特征图。RGB图像特征在不同的光照条件下提供了更一致的上下文信息，而偏振图像特征可能受到噪声的干扰。RGB图像在不同的光照条件下提供了更一致的上下文信息，而极化图像可能受到噪声的干扰。因此，文中选择了RGB图像特征作为上下文特征的来源，以保证上下文信息的一致性。
相关性代价体：参考RAFT构建相关代价体，在纹理缺失和特征稀疏的情况下，利用偏振信息作为RGB信息的补充，从而提高立体匹配的效果：
$$\begin{array}{rl}{\mathbf{IC}}_{ijk}& =\sum _h{\mathbf{f}}_{ijh}^I\cdot {\mathbf{g}}_{ikh}^I,\mathbf{IC}\in {\mathbb{R}}^{H\times W\times W},\\ {\mathbf{PC}}_{ijk}& =\sum _h{\mathbf{f}}_{ijh}^P\cdot {\mathbf{g}}_{ikh}^P,\mathbf{PC}\in {\mathbb{R}}^{H\times W\times W},\end{array}\text{\hspace{1em}(4)}$$
其中，${\mathbf{IC}}_{ijk}$ 表示RGB相关代价体，${\mathbf{PC}}_{ijk}$ 为偏振相关代价体。分别对RGB代价体与偏振代价体下采样得到4层的代价体金字塔。

Iso-Depth Cost and Ambiguity Solver 等深代价与模糊匹配

法线的等深约束：等深度轮廓与轮廓上点的法向量的方位角分量正交。通过对深度求导并用视差代替深度可以得到方位角的近似表示： $$\tan (\phi )=\frac{f_y}{f_x}\frac{({\text{d }}_{0,-1}-{\text{d }}_{0,1})({\text{d }}_{-1,0}+{\text{d }}_{1,0})}{({\text{d }}_{-1,0}-{\text{d }}_{1,0})({\text{d }}_{0,-1}+{\text{d }}_{0,1})},\text{\hspace{1em}(5)}$$
其中 $d_{i,j}$ 为像素点 $P(u,v)$的邻域像素$P(u+i,v+j)$，$f$为焦距。

等深偏振代价：如上文所述，文中构建了一个统一的等深度代价，来显式地利用偏振的几何约束，并处理方位角φ和线偏振角$\varphi$之间的$\pi -$歧义和$\pi /2-$歧义。文中提出的等深度代价$C(\phi )$通过最小化算子将镜面反射和漫反射下的方位角代价进行了整合。此外，反射类型的歧义$R(\phi )$可以由以下方式解决：
C s ( φ ) = [ s i n ( ϕ ) s i n ( φ ) + c o s ( ϕ ) c o s ( φ ) ] 2 , C d ( φ ) = [ s i n ( ϕ ) c o s ( φ ) − c o s ( ϕ ) s i n ( φ ) ] 2 , C ( φ ) = min ⁡ { C s ( φ ) , C d ( φ ) } , R ( φ ) = arg ⁡ min ⁡ { C s ( φ ) , C d ( φ ) } , (6) \begin{aligned} &\mathbf{C}_{s}(\varphi)=\left[sin\left(\phi\right)sin\left(\varphi\right)+cos\left(\phi\right)cos\left(\varphi\right)\right]^{2}, \\ &\begin{aligned}\mathbf{C}_d(\varphi)=\left[sin\left(\phi\right)cos\left(\varphi\right)-cos\left(\phi\right)sin\left(\varphi\right)\right]^2,\end{aligned} \\ &\mathbf{C}(\varphi)=\min\left\{\mathbf{C}_s(\varphi),\mathbf{C}_d(\varphi)\right\}, \\ &\begin{aligned}\mathbf{R}(\varphi)=\arg\min\left\{\mathbf{C}_s(\varphi),\mathbf{C}_d(\varphi)\right\},\end{aligned} \end{aligned}\tag{6} ​Cs​(φ)=[sin(ϕ)sin(φ)+cos(ϕ)cos(φ)]2,Cd​(φ)=[sin(ϕ)cos(φ)−cos(ϕ)sin(φ)]2,​C(φ)=min{Cs​(φ),Cd​(φ)},R(φ)=argmin{Cs​(φ),Cd​(φ)},​​(6)
其中，$C_d$和$C_s$分别表示漫反射和镜面反射的代价。
虚拟视差和虚拟相关特征：为了抑制偏振噪声引起的代价扰动，并充分利用偏振提供的等深度约束，文中根据等深度代价计算虚拟视差，并生成相应的虚拟相关特征。虚拟视差和虚拟相关特征可以用于优化GRU中的视差细化，优化GRU是双GRU架构的一部分。为了区分不同的视差，文中将在更新块中不断更新的视差称为实际视差$d_a$，把根据等深度代价的梯度和迭代更新的步长$\alpha$计算的视差称为虚拟视差$d_v$。虚拟视差的计算公式如下：

$$d_v=d_a-\alpha {\nabla }_d\mathbf{C}(\phi ,d).\text{\hspace{1em}(7)}$$

Hybrid GRU-based Update Operator 混合GRU更新单元

   文中使用混合GRU单元来挖掘多源信息并更新视差图。如图2所示：

   多源上下文信息与集合信息被送入到更新块中融合，并基于两个关联代价体金字塔提取多源相似性视觉特征 。最后，将真实与虚拟视觉相关特征送入双GRU单元循环优化视差结果。此外，虚拟视差和相关的虚拟相关特征是根据等深度代价生成的，用于间接地指导优化过程。
级联双GRU结构：文中作者提出级联的双GRU结构用于融合等深代价与视觉相似性。级联的双GRU架构由一个回归GRU和一个优化GRU组成。在回归GRU中，视差由实际视差的多域相关特征回归计算得到，这些特征利用了RGB和偏振图像的相似性，为后续的优化提供了一个初始预测。在优化GRU中，等深度代价直接作为输入并通过虚拟相关特征以一种间接的方式融入。优化GRU融合了几何约束，并进一步纠正了视差。
  文中基于虚拟相关特征来引入等深度代价，而不是直接用代价梯度计算的增量来更新视差，这样可以避免传统优化过程中的以下困难：（1）将与上下文信息耦合的匹配问题显式地转化为优化问题。（2）由于优化问题的严重非凸性带来的优化难问题。考虑到以上的难点，文中引入一个混合优化GRU避免模型在局部收敛与抑制偏振噪声的影响。此外，级联方案可以很好地平衡视觉相似性和几何约束。通过回归和优化的级联范式，在不同的迭代中逐渐细化视差。

多源输入：基于多域信息来构造GRU的输入。级联的双GRU架构中的两个GRU的输入不同。回归GRU的输入是实际视差的多域相关特征，利用了RGB和偏振图像的相似性，为后续的优化提供了一个初始预测。优化GRU的输入是虚拟视差的多域相关特征，利用了偏振图像中的等深度代价来指导视差优化。在将多域相关特征输入到GRU之前，使用两层卷积组成的编码器分别对多域输入进行处理。最后，将多域相关特征和其他编码特征拼接后输入GRU单元，如图2所示。
更新：GRU更新单元用来循环地更新视差和代价步长。该模块包括两个GRU（门控循环单元），分别是回归GRU和优化GRU。回归GRU和优化GRU都有一个隐藏状态，隐藏状态会根据编码后的混合输入不断地更新。通过不同的头网络，可以从隐藏状态中解码出视差增量和优化步长。最后基于新的增量来更新视差，并通过上采样操作来恢复全分辨率的视差图。

---

损失函数

$$\mathbf{L}=\sum _{i=1}^N{\gamma }^{N-i}{\Vert d_{gt}-d_i\Vert }_1.\text{\hspace{1em}(8)}$$

---

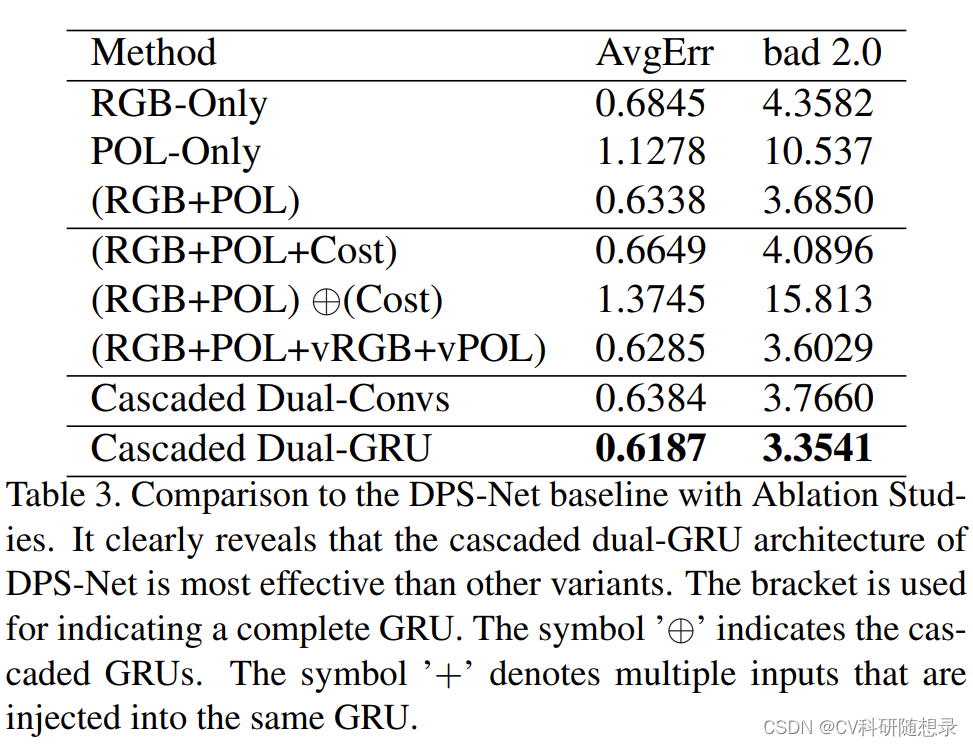
实验结果