由于本人水平有限,难免出现错漏,敬请批评改正。 更多精彩内容,可点击进入Python日常小操作专栏、OpenCV-Python小应用专栏、YOLO系列专栏、自然语言处理专栏或我的个人主页查看 YOLOv8 Ultralytics:使用Ultralytics框架训练RT-DETR实时目标检测模型 基于DETR的人脸伪装检测 YOLOv7训练自己的数据集(口罩检测) YOLOv8训练自己的数据集(足球检测) YOLOv5:TensorRT加速YOLOv5模型推理 YOLOv5:IoU、GIoU、DIoU、CIoU、EIoU 玩转Jetson Nano(五):TensorRT加速YOLOv5目标检测 YOLOv5:添加SE、CBAM、CoordAtt、ECA注意力机制 YOLOv5:yolov5s.yaml配置文件解读、增加小目标检测层 Python将COCO格式实例分割数据集转换为YOLO格式实例分割数据集 YOLOv5:使用7.0版本训练自己的实例分割模型(车辆、行人、路标、车道线等实例分割) 使用Kaggle GPU资源免费体验Stable Diffusion开源项目
Python是一种跨平台的计算机程序设计语言。是一个高层次的结合了解释性、编译性、互动性和面向对象的脚本语言。最初被设计用于编写自动化脚本(shell),随着版本的不断更新和语言新功能的添加,越多被用于独立的、大型项目的开发。 PyTorch 是一个深度学习框架,封装好了很多网络和深度学习相关的工具方便我们调用,而不用我们一个个去单独写了。它分为 CPU 和 GPU 版本,其他框架还有 TensorFlow、Caffe 等。PyTorch 是由 Facebook 人工智能研究院(FAIR)基于 Torch 推出的,它是一个基于 Python 的可续计算包,提供两个高级功能:1、具有强大的 GPU 加速的张量计算(如 NumPy);2、构建深度神经网络时的自动微分机制。 NumPy(Numerical Python的缩写)是Python语言的一个数值计算库,支持大量的维度数组与矩阵运算,此外也针对数组运算提供大量的数学函数库。NumPy的诞生极大地提升了Python进行科学计算的效率,它提供的多维数组对象和丰富的数学函数库,使得Python可以轻松地进行科学计算和数据分析。 NumPy的特点 包括:
强大的多维数组对象:NumPy提供了一个高效的多维数组对象,可以进行快速的数据处理和计算。 高效的内存管理:NumPy使用高效的内存管理,可以处理大规模的数据,并最大限度地提高了内存使用效率。 数学函数库:NumPy提供了大量的数学函数库,可以进行各种数学运算和数据处理。 广播机制:NumPy的广播机制使得在处理不同形状的数组时能够自动地进行广播,无需编写额外的循环代码。 支持GPU加速:NumPy支持GPU加速,可以充分利用GPU的计算能力进行大规模的数据处理和计算。 总之,NumPy是Python中进行科学计算和数据分析的重要工具,它提供了高效的多维数组对象和丰富的数学函数库,使得Python可以进行大规模的数据处理和高性能的科学计算。 Matplotlib是一个用于创建交互式图形的Python库。它可用于创建各种类型的图形,包括折线图、散点图、柱状图、等高线图、3D图等。Matplotlib的目标是以一种简单而直观的方式创建图形,同时保持对底层图形API的完全控制。这使得Matplotlib非常适合于数据可视化、统计、机器学习等领域。 Matplotlib的主要特点 包括:
简单易用:Matplotlib的API接口简单直观,易于学习和使用。它提供了丰富的示例代码和文档,使得用户可以快速上手。 高度可定制:Matplotlib的图形是通过一组配置参数来定义的,用户可以根据需要调整图形的样式和布局。此外,Matplotlib还提供了大量的自定义功能,如标签、图例、颜色条等。 支持多种输出格式:Matplotlib支持将图形输出为各种格式,包括PNG、JPEG、SVG、PDF等。这使得用户可以将图形导出为多种媒体格式,并进行交互式展示。 支持实时更新:Matplotlib支持实时更新图形,使得用户可以在运行时动态地更新数据和图形。 支持交互式操作:Matplotlib支持对图形进行交互式操作,如放大、缩小、平移等。这使得用户可以更方便地观察和分析数据。 总之,Matplotlib是一个功能强大的Python图形库,适用于各种类型的数据可视化任务。它简单易用、高度可定制、支持多种输出格式和交互式操作,是Python开发人员常用的数据可视化工具之一。 分段函数是一个数学函数,它在一个区间内可能有不同的表达式。具体来说,分段函数是由一些不连续的线段和常数函数组成的函数。这些线段通常在定义域内不相交,并且在每个线段上,函数的行为都由一个常数函数描述。 分段函数的优点 包括:
简化复杂函数关系:分段函数可以将复杂的函数关系拆分成多个简单的部分,使得函数的定义更加清晰和易于理解。 灵活性:分段函数可以根据不同的条件选择不同的算法或表达式来计算函数值,从而使得函数的计算更加灵活和准确。 分段函数的缺点 包括:
可读性较差:由于分段函数由多个简单的部分组成,因此可能难以理解其整体行为。 需要更多的维护:与单一的函数相比,分段函数需要更多的维护和更新。 分段函数的特性 包括:
分段连续性:在分段函数中,对于任意两个区间,该函数都是连续的。 分段可导性:在分段函数中,可以对每个单独的区间求导,以求出其斜率。 极值特性:在分段函数中,可以找到函数的极大值和极小值,但其极值不一定在函数的每个区间中。 以下是一个分段函数的例子:
f
(
x
)
=
{
2
x
−
1
:
x
≤
3
x
2
−
4
:
x
>
3
f(x) = \left\{ \begin{array}{lr} 2x - 1 & : x \leq 3 \\ x^2 - 4 & : x > 3 \end{array} \right.
f ( x ) = { 2 x − 1 x 2 − 4 : x ≤ 3 : x > 3 这个函数在
x
≤
3
x \leq 3
x ≤ 3
x
>
3
x > 3
x > 3
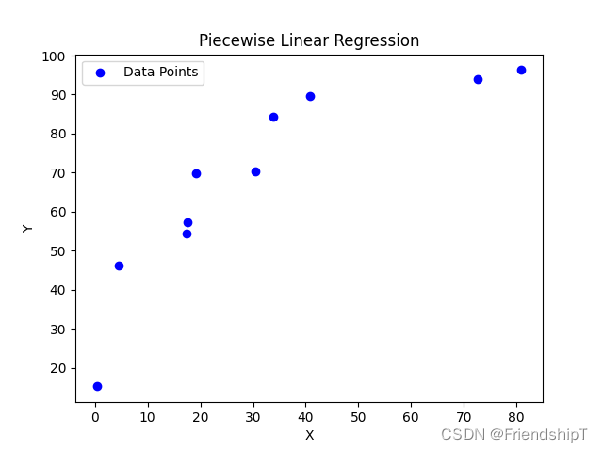
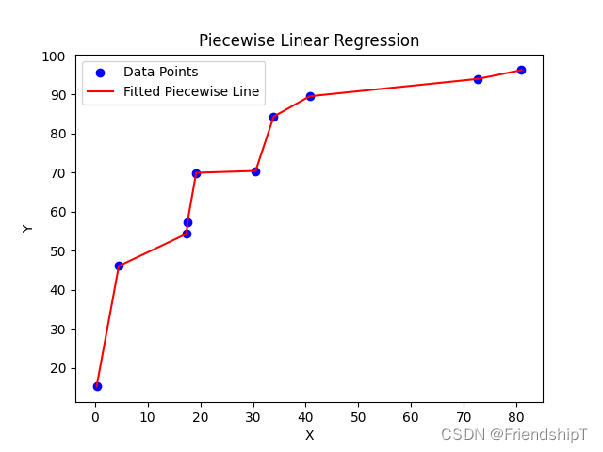
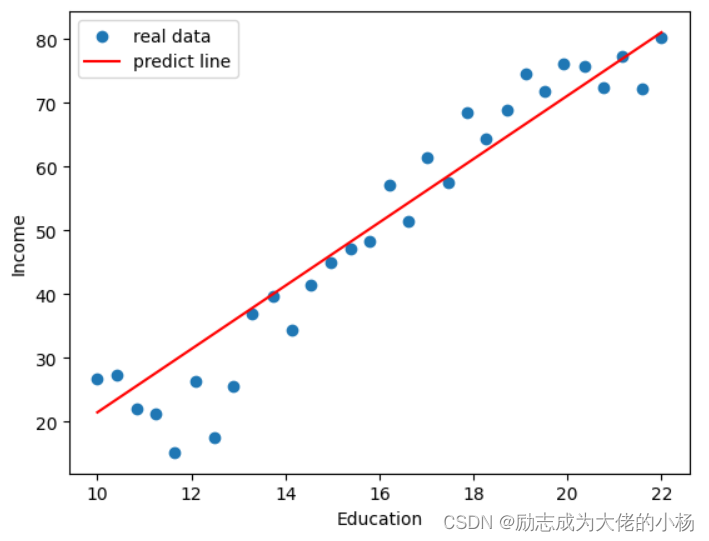
背景:将随机生成的数据,用分段函数拟合。这种方法,在某些场景下,既简单又好用 。
import numpy as np
import matplotlib. pyplot as plt
def get_x_index_in_interval ( x, Intervals) :
for i, ( a, b) in enumerate ( Intervals) :
if a < x <= b:
return i
return 0
def y_func ( x, k, b) :
y = k* x+ b
return y
def line_equation ( x1, y1, x2, y2) :
k = ( y2 - y1) / ( x2 - x1)
b = y1 - k * x1
return k, b
if __name__== "__main__" :
x = np. random. rand( 10 ) * 100
x = np. sort( x)
y = np. random. rand( 10 ) * 100
y = np. sort( y)
k_b = [ ( line_equation( x[ i] , y[ i] , x[ i+ 1 ] , y[ i+ 1 ] ) ) for i in range ( len ( x) - 1 ) ]
Intervals = [ ( x[ i] , x[ i+ 1 ] ) for i in range ( len ( y) - 1 ) ]
y_pre = [ ]
for x_value in x:
index = get_x_index_in_interval( x_value, Intervals)
y_pre. append( y_func( x_value, k_b[ index] [ 0 ] , k_b[ index] [ 1 ] ) )
plt. scatter( x, y, color= 'blue' , label= 'Data Points' )
plt. plot( x, y_pre, color= 'red' , label= 'Fitted Piecewise Line' )
plt. title( 'Piecewise Linear Regression' )
plt. xlabel( 'X' )
plt. ylabel( 'Y' )
plt. legend( )
plt. show( )
由于本人水平有限,难免出现错漏,敬请批评改正。 更多精彩内容,可点击进入Python日常小操作专栏、OpenCV-Python小应用专栏、YOLO系列专栏、自然语言处理专栏或我的个人主页查看 YOLOv8 Ultralytics:使用Ultralytics框架训练RT-DETR实时目标检测模型 基于DETR的人脸伪装检测 YOLOv7训练自己的数据集(口罩检测) YOLOv8训练自己的数据集(足球检测) YOLOv5:TensorRT加速YOLOv5模型推理 YOLOv5:IoU、GIoU、DIoU、CIoU、EIoU 玩转Jetson Nano(五):TensorRT加速YOLOv5目标检测 YOLOv5:添加SE、CBAM、CoordAtt、ECA注意力机制 YOLOv5:yolov5s.yaml配置文件解读、增加小目标检测层 Python将COCO格式实例分割数据集转换为YOLO格式实例分割数据集 YOLOv5:使用7.0版本训练自己的实例分割模型(车辆、行人、路标、车道线等实例分割) 使用Kaggle GPU资源免费体验Stable Diffusion开源项目