【AcWing每日一题】4818. 奶牛大学

news2024/11/17 3:08:36

Farmer John 计划为奶牛们新开办一所大学！

有 N 头奶牛可能会入学。

每头奶牛最多愿意支付 ci 的学费。

Farmer John 可以设定所有奶牛入学需要支付的学费。

如果这笔学费大于一头奶牛愿意支付的最高金额，那么这头奶牛就不会入学。

Farmer John 想赚尽可能多的钱，从而可以给他的讲师提供一笔可观的工资。

请求出他能赚到的钱的数量，以及此时应当收取多少学费。

输入格式
输入的第一行包含 N。

第二行包含 N 个整数 c1,c2,…,cN，其中 ci 是奶牛 i 愿意支付的最高学费金额。

输出格式
输出 Farmer John 可以赚到的最大金额以及最优情况下他应该收取的学费。如果有多个解，输出收取学费最小的解。

注意这个问题涉及到的整数可能需要使用 64 位整数型（例如，Java 中的 “long”，C/C++ 中的 “long long”）。

数据范围
1≤N≤10⁵,
1≤c_i≤10⁶。

输入样例：
4
1 6 4 6
输出样例：
12 4
样例解释
如果 Farmer John 收费 4，那么 3 头奶牛将会入学，从而使他赚取 3×4=12 的金额。

自己的想法：

一开始想的肯定是先把所有的数据存在一个地方，然后利用查找，同时把总的最大学费和最小的支付金额
这个题是离散的取值，所以想到利用散列表来存储
从后往前枚举每一个愿意交的学费
找到某一个学费，使得当前学费所得到的入学牛的数量✖当前学费的总数最大

自己的一开始的代码（TLE）：

#include<iostream>
#include<map>
using namespace std;

map<int,int> m;

int main(){
	int n, c, maxc = 0, minc = 0x7fffffff, min_single_tuition;
	long long max_total_tuition = 0;
	cin >> n;
	for(int i = 0; i < n; i++){
		cin >> c;
		m[c]++;
		if(maxc < c) maxc = c;
		if(minc > c) minc = c;
	}	
	for(int i = maxc; i >= minc; i--){
		if(m[i] != 0){
//			cout << "i = " << i << " m[i] = " << m[i] << endl;
			int total_tuition = 0;
			for(int j = i; j <= maxc; j++){
				total_tuition += i*m[j];
			}
			if(total_tuition >= max_total_tuition){
				max_total_tuition = total_tuition;
				min_single_tuition = i;
			}
		}
	}
	
	cout << max_total_tuition << " " << min_single_tuition;
	
	return 0;
}

y总的思路（最优化）：

利用数据范围猜数据复杂度，时间复杂度需要控制在需要在O(n²)以下
将所有牛按照愿意付的金额从小到大排序，那么在线段上就会产生多个点
根据题意，一定存在一个点，使得学费总额达到最大，而在这个点之前的牛都不符合要求
由于每一个愿意支付的金额的点是离散的，所以在两个点之间可能存在无数条符合条件的点符合学费的要求
我们要是的收取的学费降到最低，由于在边界上的点是纳入计算的，所以就要选择最右边的点
排序好之后，从前往后枚举
当枚举到的当前的点使得总学费金额大于前面的最大值，则更新标记
当出现两个相等的总学费时，选择更低的，所以判断时需要抛弃等号

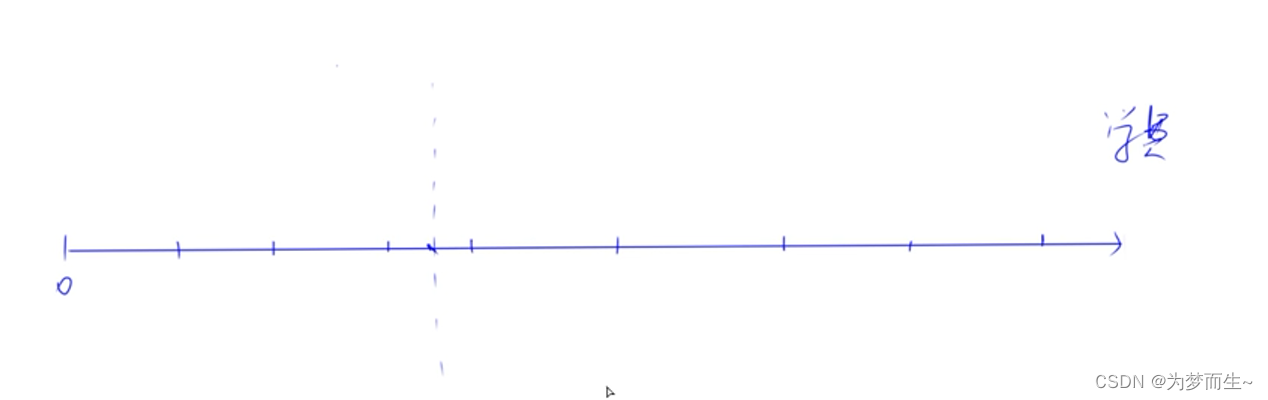
在这里插入图片描述

假设我们找到的这条线是r，那么收到的总学费应该是r ✖ 这条线右边的牛的数量

y总的代码：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 100010;

int n;
int w[N];

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &w[i]);

    sort(w, w + n);

    LL rtot = 0, rfee = 0;
    for (int i = 0; i < n; i ++ )
    {
        LL tot = (LL)w[i] * (n - i);
        if (tot > rtot)
        {
            rtot = tot;
            rfee = w[i];
        }
    }

    printf("%lld %lld\n", rtot, rfee);
    return 0;
}

//作者：yxc
//链接：https://www.acwing.com/activity/content/code/content/5046735/
//来源：AcWing
//著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

根据他的思路我找到了自己的问题：

用map比自己写的算法慢了接近一倍，每一次的插入和查找也是需要占用时间复杂度的
放弃了查找-计算的思想，只需存储和利用每一头牛愿意支付的最低学费，枚举每一个学费

自己改进的代码：

#include<iostream>
#include <algorithm>
using namespace std;

typedef long long ll;
const int N = 1e5+10;

int main(){
	int n, c[N];
	ll max_total_tuition = 0, min_single_tuition = 0x7fffffffffffffff;
	cin >> n;
	for(int i = 0; i < n; i++) cin >> c[i];
	sort(c, c+n);
	
	for(int i = 0; i < n; i++){
		ll total = (ll)c[i]*(n-i);
		if(total > max_total_tuition){
			max_total_tuition = total;
			min_single_tuition = c[i];
		}
	}
	
	cout << max_total_tuition << " " << min_single_tuition;
	
	return 0;
}