链表图中的“^”符号表示所储存内容为空。 

单循环链表

末结点的next不再指向空，而是指向头结点。

 空单向循环链表，只有头结点。

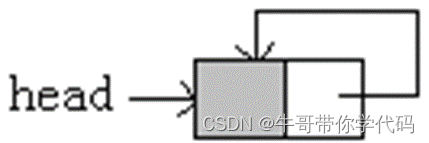
 优点：从表中任何一个结点出发，都可以顺next指针访问到所有结点。

不带头结点的单循环链表

为了循环方便，不带头结点的单循环链表居多，head直接指向首结点。

 空单向循环链表，head指向空。

 双向链表

每个结点有prior和next两个指针，分别指向直接前驱和直接后继结点

 空双向链表，只有头、尾结点。

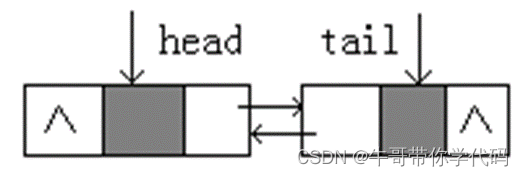
 优点：根据待查元素在前或后半段，决定自head向后还是自tail向前。

双向循环链表

不带头、尾结点的双向循环链表

 空双向链表

双向链表

插入：将元素x插入到p指针所指结点之后。

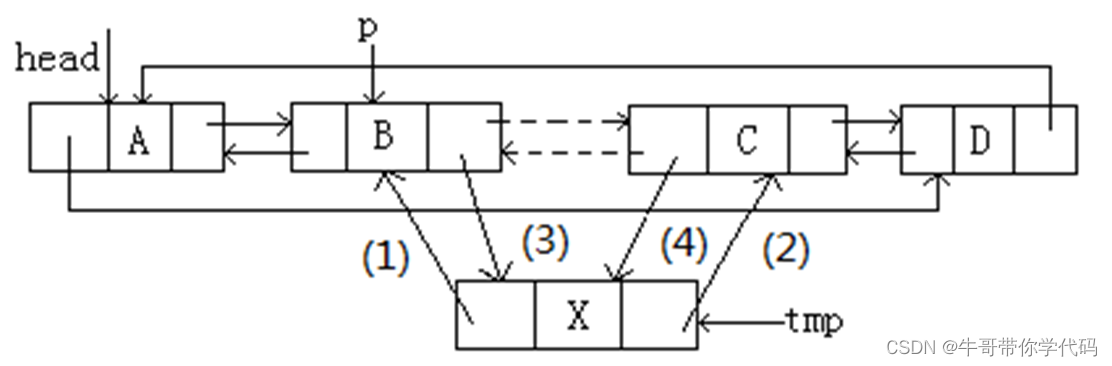
对应代码

node *tmp = new node()  //（1）

tmp->data = x;         // （2）
tmp->prior = p;        
tmp->next =p->next;    

tmp->prior->next =tmp;  // （3）
tmp->next->prior =tmp;  // （4）

 如果新结点插入在首结点位置，操作又有不同

一元多项式

在数学上，一元多项式一般表示为如下形式：

pn(x) = p0 + p1x + p2x^2 + … + pnx^n

在计算机内实现时，可以用线性表来表示:

p = ( p0，p1，p2，…， pi …，pn)，其中结点pi(0≤i≤n)表示幂为i项的系数。

一元多项式存储方法

i次幂项的系数pi存放在下标为i的数组结点中，即便pi为0，相应的数组分量也不能挪作它用。

   两个多项式的加法处理起来比第一种方法复杂。

   用数组时，要预估一个多项式的规模，分配足够的空间。

一元多项式的链式存储

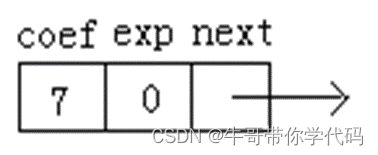
多项式如： 

A=7+3x+9x^8+5x^17

B=8x+22x^7-9x^8

 

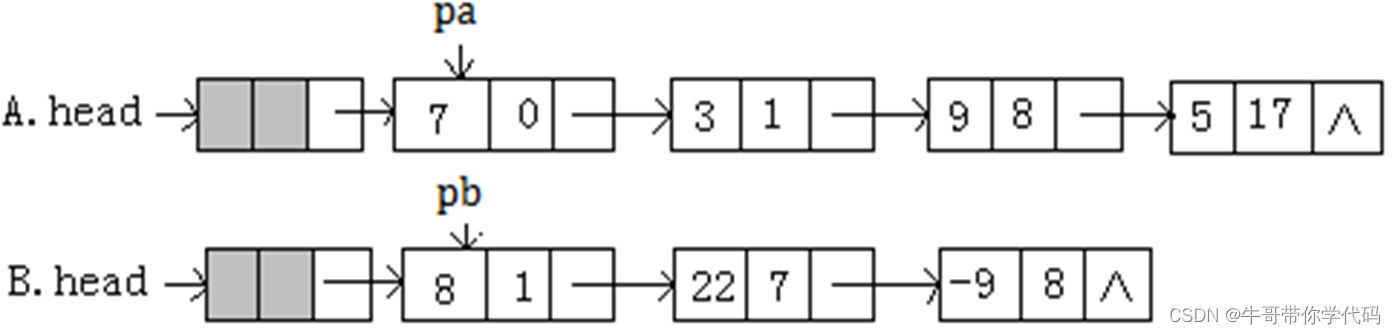
两个一元多项式相加

对pa和pb所指结点，反复执行如下操作，直至其中一个单链表中的结点全部读取完毕。

 将非空多项式单链表(可能是A的单链表，也可能是B的单链表)中的剩余结点，按序逐个创建新结点插入在单链表 C 的尾部

 多项式Polynomial 及其部分基本操作的声明、定义（polynomial.h）

#ifndef POLYNOMIAL_H_INCLUDED
#define POLYNOMIAL_H_INCLUDED

#include "linklist.h"
using namespace std;
struct Type
{  int coef;  // 系数                    分开定义结点的好处
    int exp;  // 幂指数
}

template <class elemType>
struct Node
{  elemType data;
    Node* next;
};
template <class elemType>
struct Polynomial
{
    private:
        Node<elemType>* head;
        elemType stop_flag; // 用于判断多项式输入结束。
    public:
        //从用户处获取结束标志并初始化多项式
        Polynomial(const elemType &stop);
        void getPoly(); //读入一个多项式。
        void addPoly(const Polynomial &L1, const Polynomial &L2);
          // L3=L1+l2。
        void dispPloy();//显示一个多项式
        void clear();//释放多项式空间
        ~Polynomial(){clear(); delete head;};  //注意此处析构函数~Polynominal()中的写法
};
// getStop为外部函数，即非类成员函数
template <class elemType>
void getStop(elemType &stopFlag)//从用户处获取结束标志
{
    int c,e;
    cout<<"请输入系数、指数对作为结束标志,如(0,0): ";
    cin>>c>>e;
    stopFlag.coef = c;
    stopFlag.exp = e;
}
template <class elemType>
Polynomial<elemType>::Polynomial(const elemType &stop)
                                                          //初始化多项式
{   head = new Node<elemType>();
    stop_flag.coef = stop.coef;
    stop_flag.exp = stop.exp;
}
 

template <class elemType>
void Polynomial<elemType>::getPoly() //读入一个多项式
{   Node<elemType> *p, *tmp;
    elemType e;
    p=head;
    cout<<“请按照指数从小到大输入系数、指数对，” <<最后输入结束标志对结束：\n";
    cin>>e.coef>>e.exp;
 
    while (true)
    {
        if ((e.coef==stop_flag.coef)&&(e.exp==stop_flag.exp)) break;
        tmp = new Node<elemType>();
        tmp->data.coef = e.coef;
        tmp->data.exp = e.exp;
        tmp->next = NULL;
        p->next = tmp;
        p=tmp;

        cin>>e.coef>>e.exp;
    }
}
template <class elemType>
void Polynomial<elemType>::addPoly(const Polynomial &La, const Polynomial &Lb)// La+Lb
{此处省略}

多项式Polynomial相加主程序（main.cpp）

#include <iostream>
#include "polynomial.h"
using namespace std;
int main()
{
	Type stop_flag;
	getStop(stop_flag);  //读入停止标志对
	Polynomial<Type> L1(stop_flag), L2(stop_flag), L3(stop_flag);
    	L1.getPoly(); //读入第一个多项式
    	L2.getPoly(); //读入第二个多项式
    	L3.addPoly(L1,L2); //L1 = L2 +L3
   	L3.dispPloy(); //显示多项式L3的内容
	return 0;
}