题目链接

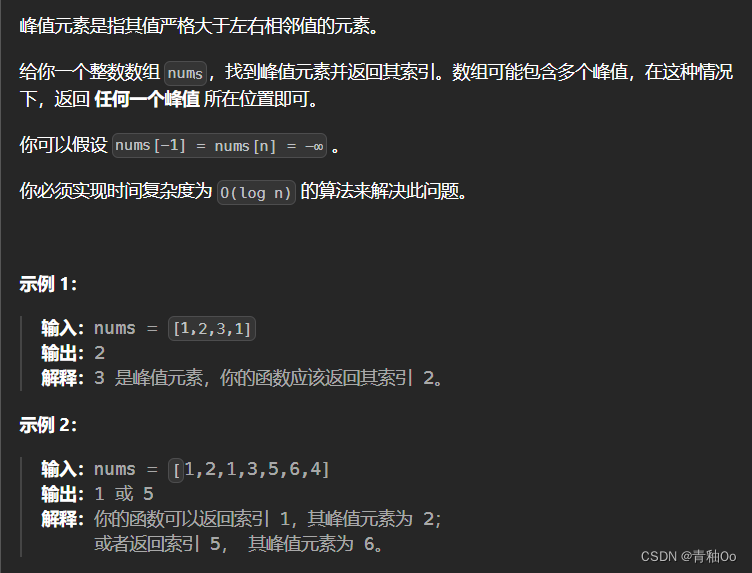
寻找峰值

题目描述

注意点

• 数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可
• 对于所有有效的 i 都有 nums[i] != nums[i + 1]
• 可以假设 nums[-1] = nums[n] = -∞

解答思路

• 可以根据二分查找保证在O(log n)的时间复杂度找到峰值，思路为：数值越大，该数字越有可能是一个峰值，在进行二分查找时，如果中间的数字比其相邻右侧的数字大（左侧也是类似的思想），则其峰值更有可能在二分查找的左侧；相对的，如果中间的数字比其相邻右侧的数字小，则其峰值更有可能在二分查找的右侧，直到左右指针相遇的位置就一定是一个峰值

代码

class Solution {
    public int findPeakElement(int[] nums) {
        int n = nums.length;
        int left = 0, right = n - 1;
        while (left < right) {
            int mid = (left + right) / 2;
            if (nums[mid] > nums[mid + 1]) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }
}

关键点

• 二分查找的思想
• 本题转换成二分查找的思路