46. 全排列 - 力扣（LeetCode）

回溯法

采用试错的思想，它尝试分步的去解决一个问题。在分步解决问题的过程中，当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现，在反复重复上述的步骤后可能出现两种情况：

• 找到一个可能存在的正确的答案；
• 在尝试了所有可能的分步方法后宣告该问题没有答案。

思路

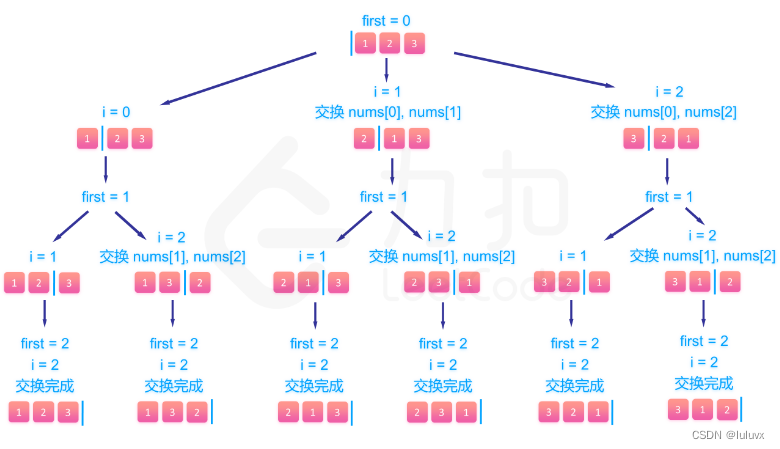
用 n 表示数组 nums 的长度。创建列表 temp 用于存储当前排列，将数组 nums中的每个元素依次加入 temp，然后根据 temp 生成全排列。

为了得到数组 nums 的全排列，需要依次确定排列中的每个位置的元素，可以通过交换 temp 中的元素实现。对于 0≤ index <n，按照下标 index 从小到大的顺序依次确定每个 temp[index] 的值，即可得到一个排列。

1. 当 index = 0 时，可以将 temp[0]和任意一个元素交换（包括和自身交换），经过一次交换之后即可确定当前排列中 temp[0]的值。
2. 当 index>0 时，如果当前排列中 temp[0] 到 temp[index−1] 的值都已经确定，则可以将 temp[index]和尚未确定的任意一个元素交换（包括和自身交换），经过一次交换之后即可确定当前排列中 temp[index]的值。

由于当 index = 0 时，排列中的所有元素都尚未确定，因此对于任意 0≤ index < n，都可以将 temp[index] 和任意一个下标大于等于 index 的元素交换，经过一次交换之后即可确定当前排列中 temp[index] 的值。

使用回溯得到全排列。用 index 表示当前下标，初始时 index = 0，具体做法如下。

如果 index = n，则当前排列中的所有元素都已经确定，将当前排列添加到结果列表中。

如果 index< n ，则对于每个 index≤ i < n，执行如下操作。

1. 将 temp[index] 和 temp[i] 的值交换，然后将 index+1 作为当前下标继续搜索。
2. 将 temp[index]和 temp[i]的值再次交换，恢复到交换之前的状态。

当每个下标对应的所有可能的值都遍历结束时，即可得到数组 nums 的全排列。

代码实现

public class Solution {
    IList<IList<int>> permutations = new List<IList<int>>();
    IList<int> temp = new List<int>();
    int n;

    public IList<IList<int>> Permute(int[] nums) {
        foreach(int num in nums)
        {
            temp.Add(num);
        }
        n = nums.Length;
        Backtrack(0);
        return permutations;
    }

    public void Backtrack(int index)
    {
        if(index == n)
            permutations.Add(new List<int>(temp));
        else
        {
            for(int i = index; i < n; i++)
            {
                Swap(temp, index, i);
                Backtrack(index + 1);
                Swap(temp, index, i);
            }
        }
    }
    public void Swap(IList<int> temp, int index1, int index2)
    {
        int curr = temp[index1];
        temp[index1] = temp[index2];
        temp[index2] = curr;
    }
}