性质
——性质——
一、是什么
(1)本质:判断一定范围内的对象是否具备某个性质的命题就是性质命题(直言命题)。直言命题是断定事物/对象是否具有某种性质的命题。直言命题在结构上由主项、谓项、联项和量项组成。
(2)量项/量词:量项指的是性质命题判断的范围。量词,即数量词,逻辑中常用“所有"和“有的”表示。
(3)主项/主语:主项指的是性质命题判断的对象。主语,指性质命题的判断对象。
(4)谓项/谓语:谓项指的是该对象是具有某个性质还是不具有某个性质。谓语,指判断对象所具有或不具有的性质。
注意点:
(1)“有的”含义
“有的”的意思并不是“部分”,它是一个存在量词,数量是从“1”到“所有”都有可能。
(2)量词的位置
“全称命题”的量词“所有"和“特称命题”的量词“有的”,应该修饰主语,而不是宾语。
(3)“一个”不一定是“一个”:一个男人需要努力学习。这里的“一个”指的是“任何”。
2.分类
(1)全称肯定命题:所有S都是P,公式为
S
→
P
S→P
S→P,记为SAP,缩写为A。
(2)全称否定命题:所有S都不是P,公式为
S
→
┐
P
S→┐P
S→┐P,记为SEP,缩写为E。
(3)特称肯定命题:有的S是P,公式为
有的
S
→
P
有的S→P
有的S→P,记为SIP,缩写为I。
(4)特称否定命题:有的S不是P,公式为
有的
S
→
┐
P
有的S→┐P
有的S→┐P,记为SOP,缩写为O。
(5)单称肯定命题:某个S是P,公式为
某个
S
→
P
某个S→P
某个S→P,记为SaP,缩写为a。
(6)单称否定命题:某个S不是P,公式为
某个
S
→
┐
P
某个S→┐P
某个S→┐P,记为SeP,缩写为e。
注意:
① 在考试中,判断一个命题是否是性质命题,首先要看是否有“范围”,其次是看其含义是否有强调某事物是否具有某性质。
② 在汉语表达中,“是"不是”在某些情况下是可以省略的,比如“所有金属都能导电”,就意味着"“所有金属都是能导电的”。
③ “有的”代表数量大于或等于1。
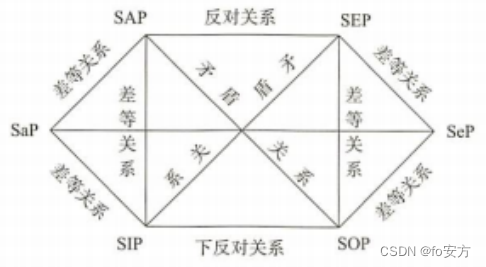
(1)矛盾关系(A—O、E—I、 a—e)不同真(此真彼必假),不同假(此假彼必真)。——【口诀:对角成矛盾,上真推下真,下假推上假,其余推不出。】
A—O:“所有同学考试都及格”与“有些同学考试不及格”。
E—I:“所有同学考试都不及格”与“有些同学考试及格”。
a—e:“小王同学考试及格”与“小王同学考试不及格”。
总结:矛盾关系存在于SAP 和SOP之间、SEP和SIP之间、SaP和SeP之间。
(2)反对关系(A—E)可以同假,不可同真,必有一假。
A—E:“所有同学考试都及格”与“所有同学考试都不及格”。
总结:反对关系存在于SAP和SEP之间。
(3)下反对关系(I—O)可以同真,不可同假,必有一真。
I—O:“有些同学考试及格”与“有些同学考试不及格”。
总结:下反对关系存在于SIP和SOP之间。
(4)差等关系(A—I、E—O)全真特必真,特真全不定;全假特不定,特假全必假。
① A—I全真特必真:“所有同学考试都及格”为真时,“有些同学考试及格”也必然为真;特真全不定:“有些同学考试及格”为真时,“所有同学考试都及格”真假不确定。
② E—О全真特必真:“所有同学考试都不及格”为真时,“有些同学考试不及格”也必然为真;特真全不定:“有些同学考试不及格”为真时,“所有同学考试都不及格”真假不确定。
③ A—I全假特不定:“所有同学考试都及格”为假时,“有些同学考试及格”真假不确定;特假全必假:“有些同学考试及格”为假时,“所有同学考试都及格”也必然为假。
④ E—О全假特不定:“所有同学考试都不及格”为假时,“有些同学考试不及格”真假不确定;特假全必假:“有些同学考试不及格”为假时,“所有同学考试都不及格”也必然为假。
1.换质推理
直言命题A、E、I、O的换质推理规则如下:
(1)“所有S是P”可以换质为“所有S不是非P”;
(2)“所有S不是P”可以换质为“所有S是非P";
(3)“有些S是P”可以换质为“有些S不是非P”;
(4)“有些S不是P”可以换质为“有些S是非P"。
2.换位推理
直言命题A、E、I、O的换位推理规则如下:
(1)“所有S是P”可以换位为“有些P是S”;
(2)“所有S不是P”可以换位为“所有P不是S";
(3)“有些S是P”可以换位为“有些Р是S";
(4)“有些S不是P”不能换位。
二、关系——【性质的关系:矛盾,上下反对,推理
矛盾
⟹
\Longrightarrow
⟹ 一真一假
⟹
\Longrightarrow
⟹ 一真另必假,一假另必真,必然一真一假
上反对
⟹
\Longrightarrow
⟹至少一假
⟹
\Longrightarrow
⟹ 一真另必假,一假另不定,至少一假
⟹
\Longrightarrow
⟹ 上是所有
下反对
⟹
\Longrightarrow
⟹至少一真
⟹
\Longrightarrow
⟹ 一假另必真,一真另不定,至少一真
⟹
\Longrightarrow
⟹ 下是有的
推理
⟹
\Longrightarrow
⟹逆否换位:所有可逆否,还可推有的,有的仅换位,其余推不出;联立:共同话题,有的出发,逆否换位,首尾联立。
⟹
\Longrightarrow
⟹ 】
性质命题之间有四大关系,分别是:矛盾关系、反对关系、下反对关系、推理关系。把六个性质命题放入到六边形的六个顶点,就构成了性质命题的对当矩阵/对当关系图。——【对当关系
矛盾关系,一真一假;一真另必假,一假另必真。
反对关系,至少一假;一真另必假,一假另不定。
下反对关系,至少一真;一假另必真,一真另不定。
推理关系,上真下必真,下假上必假;反之则不定。
】
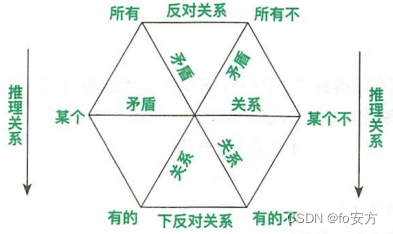
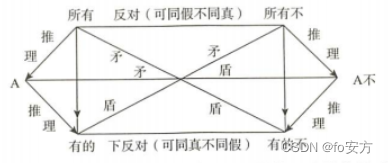
1.矛盾关系——【矛盾关系有三组,一真另必假,一假另必真】
对象:(1)所有、有的不(“所有”与“有的不”矛盾);(2)所有不、有的;(3)某个、某个不。
口诀:矛盾关系,一真另必假,一假另必真,必然一真一假 or 矛盾关系,一真一假;一真另必假,一假另必真
公式:并非所有=有的不;
并非所有不=有的;
并非有的=所有不;
并非有的不=所有。——【口诀:并非之后,所有有的互相变,必然可能互相变,肯定否定互相变。】——【口诀:并非之后,所有有的,必然可能,肯定否定互相变。】
2.上反对关系——【上是所有,至少一假】
对象:所有、所有不。
关系:“所有”和“所有不”的真假情况可能是一真一假,也可能是两假,即二者至少一假。把这种关系称为反对关系。
口诀:反对关系,一真另必假,一假另不定,至少一假 or 反对关系,至少一假,一真另必假,一假另不定
TIPS:
注意,“所有”和“某个不”,“所有不”和“某个”也是反对关系。但是真题中考查不多。
3.下反对关系——【下是有的,至少一真】
对象:有的、有的不。
关系:“有的”和“有的不"的真假情况可能是一真一假,也可能是两真,即二者至少一真。把这种关系称为下反对关系。
口诀:下反对关系,一假另必真,一真另不定,至少一真 or 下反对关系,至少一真,一假另必真,一真另不定
TIPS:
注意,“有的”和“某个不”,“有的不”和“某个”也是下反对关系。但是真题中考查不多。
4 推理关系
对象:(1)所有、某个、有的;(2)所有不、某个不、有的不。
关系:所有→某个→有的;所有不→某个不→有的不。
口诀:推理关系,上真下真,下假上假,上假下不定,下真上不定 or 推理关系,上真下必真,下假上必假;反之则不定
(1)逆否换位——【性质命题的逆否换位:所有可逆否,还可推有的,有的仅换位,其余推不出】
① 所有可逆否
若已知“所有人都会死”,则我们可以得到“所有不会死的不是人”。用公式表达就是:
S
→
P
=
┐
P
→
┐
S
S→P=┐P→┐S
S→P=┐P→┐S(逆否推理),
S
→
┐
P
=
P
→
┐
S
S→┐P=P→┐S
S→┐P=P→┐S
②
有的
有的
有的仅换位
若“有的研究生爱喝奶茶”为真,我们也可以得到“有的爱喝奶茶的是研究生”。故有如下公式:
有的
S
→
P
=
有的
P
→
S
有的S→P=有的P→S
有的S→P=有的P→S,
有的
S
→
┐
P
=
有的
┐
P
→
S
有的S→┐P=有的┐P→S
有的S→┐P=有的┐P→S。
该推理中仅仅交换了S和P的位置,其余均未改变,因此,我们将其叫作
有的
S
→
P
有的S→P
有的S→P的换位推理。
③
所有
所有
所有推
有的
有的
有的
但要注意,根据对当矩阵可知,当“所有研究生爱喝奶茶”为真时,可以推出“有的研究生爱喝奶茶”,再结合上面的换位性质可知“有的爱喝奶茶的是研究生”。故有如下公式:
S
→
P
⟹
有的
S
→
P
=
有的
P
→
S
S→P\Longrightarrow有的S→P=有的P→S
S→P⟹有的S→P=有的P→S。
④ 其余推不出
1)
S
→
P
S→P
S→P无法推出
P
→
S
P→S
P→S。
例如,“所有湖北人是中国人”为真,无法推出“所有中国人是湖北人”为真,因为,还存在其他地方的人是中国人。
2)
S
→
P
S→P
S→P无法推出
┐
S
→
┐
P
┐S→┐ P
┐S→┐P。
例如,“所有湖北人是中国人”为真,无法推出“所有不是湖北人的都不是中国人”为真,理由同上。
3)
有的
S
→
P
有的S→P
有的S→P无法推出否定结论。
例如,“有的湖北人是中国人”为真,无法推出“有的不是中国人的是湖北人”为真,因为,不是中国人肯定就不是湖北人。
(2)联立规则——【性质命题的联立:共同话题,有的出发,逆否换位,首尾联立】
①
A
→
B
,
B
→
C
A→B,B→C
A→B,B→C
⟹
\Longrightarrow
⟹
A
→
B
→
C
A→B→C
A→B→C
②
A
→
B
,
C
→
┐
B
A→B,C→┐B
A→B,C→┐B
⟹
\Longrightarrow
⟹
A
→
B
→
┐
C
A→B→┐C
A→B→┐C
③
A
→
B
,
┐
A
→
C
A→B,┐A→C
A→B,┐A→C
⟹
\Longrightarrow
⟹
┐
C
→
A
→
B
┐C→A→B
┐C→A→B
④
有的
A
→
B
,
B
→
C
有的A→B,B→C
有的A→B,B→C
⟹
\Longrightarrow
⟹
有的
A
→
B
→
C
有的A→B→C
有的A→B→C
⑤
有的
A
→
B
,
C
→
┐
B
有的A→B,C→┐B
有的A→B,C→┐B
⟹
\Longrightarrow
⟹
有的
A
→
B
→
┐
C
有的A→B→┐C
有的A→B→┐C
⑥
有的
B
→
A
,
B
→
C
有的B→A,B→C
有的B→A,B→C
⟹
\Longrightarrow
⟹
有的
A
→
B
→
C
有的A→B→C
有的A→B→C
⑦
有的
B
→
A
,
C
→
┐
B
有的B→A,C→┐B
有的B→A,C→┐B
⟹
\Longrightarrow
⟹
有的
A
→
B
→
┐
C
有的A→B→┐C
有的A→B→┐C
5.等价及变形
(1)
S
→
P
S→P
S→P的等价及变形推理
公式1:
S
→
P
=
┐
P
→
┐
S
S→P=┐P→┐S
S→P=┐P→┐S
公式2:
S
→
P
S→P
S→P
⟹
\Longrightarrow
⟹有的
S
→
P
S→P
S→P
⟹
\Longrightarrow
⟹ 有的
P
→
S
P→S
P→S
(2)有的
S
→
P
S→P
S→P的等价及变形推理
公式:有的
S
→
P
S→P
S→P=有的
P
→
S
P→S
P→S
6.负命题/并非命题——【并非之后,所有有的互相变,必然可能互相变,肯定否定互相变。】
(1)“并非所有”等价于“有的不”
【易错点】“并非所有”等价于“有的不”,这是一种简略的写法,补充完整应该是“并非所有+主语(即判断对象)+肯定的谓语动词”=“有的+主语(即判断对象)+否定的谓语动词”。
(2)“并非所有不”等价于“有的”
(3)“并非有的”等价于“所有不”
(4)“并非有的不”等价于“所有”
“并非”十“性质命题”,等价于去掉前面的“并非”,再将原“性质命题”进行如下变化:
肯定变否定,否定变肯定;所有变有的,有的变所有。
三段论
三段论:所有,有的(考2题)(以性质命题为基础,最常用推理)——【三段论:
题干出现多直言,优先考虑三段论,
一否得否特得特,否特成双结论难,
定义判别先排除,寻找结论作拆分,
出现特称放句首,特称换位构桥梁。】
——【】
三段论的定义
三段论是由包含着一个共同词项的两个直言命题推出一个新的直言命题的推理。三段论在结构上包括大项、小项和中项。
三段论的基本构成
大前提:所有M都是Р(也可以写作MAP);
小前提:所有S都是M(也可以写作SAM);
结论:所有S都是P(也可以写作SAP)。
其中,S是小项,P是大项,M是中项。
三段论的三种命题形式
(1)A→B,因此,A→C。要求补充一个条件,使上述结论成立。
显然需要补充:B→C,串联得:A→B→C。
(2)有的A→B,因此,有的A→C。要求补充一个条件,使上述结论成立。
显然需要补充:B–C,串联得:有的A-B-C。
(3)有的A→B,因此,有的B→C。要求补充一个条件,使上述结论成立。
由“有的A→B”=“有的B→A”,需要补充:A→C,串联得:有的B→A→C。
说明:观察上述三种命题方式,可发现以下共同规律:
(1)如果出现“有的”,则一定只出现2次,一次在前提中,一次在结论中。
(2)A、B、C三个词各出现2次。——【】
三段论的常见考法
1.给出一个前提和结论,要求补充另一个前提。——【补前提】
2.给出前提,要求按照三段论推理方法推出结论。——【推结论】
判别技巧:当题干中出现多个直言命题时,考虑用三段论解题。
三段论的解题规则
1.寻找结论作拆分:如果要补充前提,那么就需要把结论进行拆分。
例如,结论是:有的S→P。为了与已知前提构建逻辑链,需要将其拆分成:有的S→( )→P。然后将已知前提整理成S→M或者M→Р的样式,将M补充进括号。此时,需要补充的前提就是M→P或者S→M。
2.特称换位构桥梁:在用两个直言命题推出结论的时候,要找到两个前提的中项M,以它为桥梁构建成一条逻辑链。如果无法直接串联,需要将其中的特称命题换位,以便使之成为桥梁,构成逻辑链。
3.出现特称放句首:如果存在特称命题“有的”,需要把含“有的”的词项放在结论逻辑链的开头。
三段论的基本结构
1.基本结构1(最简单,不考):
所有A是B
所有B是C
得:所有A是C
2.基本结构2:(错误三段论中考察最多)
所有A是B
有的B是C
得:无结论(错误点:中项不周延)
3.基本结构3:
有的A是B
所有B是C
得:有的A是C
4.基本结构4:
所有A都不是B
有的A是C
得:有的C不是B
5.基本结构5:(常识可判断)
有的A是B
有的B是C
得:无结论
三段论的正确规则——【1.必然包含三个概念,每个出现两次。2.中项至少周延一次。3.特推特,否推否,两特两否无结论。】
1.必然包含三个概念,每个出现两次。
2.中项至少周延一次。
(“所有A”为A周延;“有的A”为A不周延)
3.特推特,否推否,两特两否无结论。
(1)特推特:“有的”推“有的”,即前提有一个“有的”,结论必为有一个“有的”;
有的A是B
所有B是C
得:有的A是C
(2)否推否:“否定前提”推“否定结论”,前提有一个“否定”,结论必有一个“否定”。
(3)两特两否无结论:前提为两个“有的”或两个“否定”,无结论。
例-两否
所有A不是B
所有B不是C
得:无法确定A,C之间关系,无结论。
三段论的推理规则——【一否得否,特得特,否特成双,结论难。】
口诀:一否得否,特得特,否特成双,结论难。
上述口诀的意思是:
(1)如果前提中有一个是否定命题,那么结论就是否定命题。
两个否定前提推不出确定的结论。因此,在有效的三段论推理中,如果两个前提有一个是否定命题,那么另一个必须是肯定命题;如果结论是否定命题,那么可以推断前提有且只有一个是否定命题;如果结论是肯定命题,那么可以推断两个前提都是肯定命题。
(2)如果前提中有一个是特称命题,那么结论就是特称命题。
两个特称命题也推不出确定的结论。因此,在有效的三段论推理中,如果两个前提有一个是特称命题,则另一个必须是全称命题;如果结论是特称命题,那么可以推断前提有且只有一个是特称命题;如果结论是全称命题,那么可以推断两个前提都是全称命题。
三段论的解题方法
一、考点1:补前提
1.列出已知前提和结论。
2.依据三段论规则补前提。
第一种情况:
(1)第一步:规则③特推特,否推否,两特两否无结论。得:“不”“所有”;
前提: 有的A是B 结论:有的A不是C
推前提:所有__不__
(2)第二步:规则①概念现两次,得有两种可能:
推前提:所有B不是C。所有C不是B。
(3)第三步:规则②中项要周延:
中项(前提出现两次)是B,要“所有”,得所有B不是C。
第二种情况:
(1)第一步:由规则③,特推特,否推否,两特两否无结论。
前提:所有A都B 结论:有的C不A
推前提:有的___不___
(2)第二步:由规则①,得有两种可能:
有的B不C。有的C不B。
(3)第三步:由规则②,中项要周延:
中项是B,要周延,不能“有的”,得前提为:有的C不B。
二、考点2:推结论
所有A是B
所有B是C
得:所有A是C
三段论的秒杀方法
“开心消乐”法:
已知:有的A→B,B→C,可以推出:有的A→C。
隐含三段论问题符合“词项成对出现”原则。因此,多数隐含三段论问题可以把成对的项直接消掉,余下的项用箭头串联一般就是答案。