文章目录
- 上一篇
- 推理概述
- 自然演绎推理
- 合适公式
- 归结演绎推理
- 归结原理
- 归结反演
- 提升归结效率
- 下一篇
上一篇
人工智能原理复习–知识表示(二)
推理概述
推理就是按某种策略由已知判断推出另一判断的思维过程
分类:
- 演绎推理、归纳推理、默认推理
- 确定推理、不确定推理
- 单调推理、非单调推理
冲突消解策略:
- 按就近原则排序
- 按已知事实的新鲜度排序
- 按匹配度排序
- 按领域问题特点排序
- 按上下文限制排序
- 按条件个数排序
- 按规则的次序排序
自然演绎推理
自然演绎推理是指从一组已知的事实出发,直接运用命题逻辑或谓词逻辑中的推理规则推出结论的过程。
推理规则:
- P规则:在推理的任何步骤上都可引入前提,继续进行推理
- T规则:推理时,如果前面步骤中有一个或多个公式永真蕴含公式S,则可把S引入推理过程中。
- 反证法: P → Q P \rightarrow Q P→Q当且仅当前真后假的时候时不可满足的
- 假言推理:如果P为真, P → Q P \rightarrow Q P→Q,则Q为真
- 拒取式推理:如果Q为假, P → Q P \rightarrow Q P→Q,则P也为假
注意:避免产生的两类错误:
- 如果Q为真,那么 P → Q P \rightarrow Q P→Q, 不能推出P的真值
- 如果P为假,那么 P → Q P \rightarrow Q P→Q, 不能推出Q的真假
合适公式
遵从下列递归定义的是合适公式
单一谓词公式是合适公式,使用
¬
、
∧
、
∨
、
→
、
↔
、
∃
、
∀
\lnot、\land、\lor、\rightarrow、\leftrightarrow、\exist、\forall
¬、∧、∨、→、↔、∃、∀后仍是合适公式
合适公式的性质
重点:
- P → Q ⇔ ¬ P ∨ Q P \rightarrow Q \Leftrightarrow \lnot P \lor Q P→Q⇔¬P∨Q
- 逆否: P → Q ⇔ ¬ Q → ¬ P P \rightarrow Q \Leftrightarrow \lnot Q \rightarrow \lnot P P→Q⇔¬Q→¬P
- 摩根定律: ( ¬ P ∨ ¬ Q ) ⇔ ¬ ( P ∧ Q ) (\neg P \lor \neg Q) \Leftrightarrow \neg (P \land Q) (¬P∨¬Q)⇔¬(P∧Q)
- 量词否定: ¬ ( ∃ x ) P ( x ) ⇔ ( ∀ x ) ( ¬ P ( x ) ) \lnot (\exist x)P(x) \Leftrightarrow (\forall x)(\lnot P(x)) ¬(∃x)P(x)⇔(∀x)(¬P(x))任意存在互换同理
- 量词分配:可以将量词分配到括号里
合适公式的标准化
- 首先要以量词前束范式来表示合适公式,前束范式就是在前面将变量量词罗列出来,后面括号里没有任何量词的谓词公式。
- Skolem标准型,在前束范式的基础上,消除存在量词,而拿来保证公式的永假性的函数称为Skolem函数,无参时称为Skolem常量,从一阶逻辑公式变换到Skolem标准型不是等值变换,但是保持永假性。
- 要求母式(即后面的公式化为合取范式)
- 消去多余的量词
消去蕴含符号减少否定的辖域(内移否定符号)变量标准化(变量换名)(名字相同,辖域不同需要换成不同的名字)消去存在量词(Skolem变换)- 全称量词前束化
- 消去全称量词
- 把母式转化为合取范式
消去存在量词方法:
- 如果
∃
\exist
∃在
∀
\forall
∀的辖域内
( ∀ z ) ( ∃ w ) [ ¬ Q ( x , z ) ∧ P ( z , w ) ] (\forall z)(\exists w)[\lnot Q(x, z) \land P(z, w)] (∀z)(∃w)[¬Q(x,z)∧P(z,w)]
如果w依赖于z则可以用w = g(z)来定义这种依赖关系,用g(z)来取代约束变量w,消去存在量词 ∃ w \exist w ∃w
( ∀ z ) [ ¬ Q ( x , z ) ∨ P ( z , g ( z ) ) ] (\forall z)[\lnot Q(x,z) \lor P(z, g(z))] (∀z)[¬Q(x,z)∨P(z,g(z))] - 如果
∃
\exist
∃在多个
∀
\forall
∀的辖域内
( ∀ x ) ( ∀ y ) ( ∀ z ) ( ∃ w ) P ( x , y , z , w ) (\forall x)(\forall y)(\forall z)(\exist w)P(x, y, z, w) (∀x)(∀y)(∀z)(∃w)P(x,y,z,w)
则用多元函数g(x, y, z)来取代w
( ∀ x ) ( ∀ y ) ( ∀ z ) ( ∃ w ) P ( x , y , z , g ( x , y , z ) ) (\forall x)(\forall y)(\forall z)(\exist w)P(x, y, z, g(x, y, z)) (∀x)(∀y)(∀z)(∃w)P(x,y,z,g(x,y,z)) - 如果
∃
\exist
∃在
∀
\forall
∀的辖域外
( ∃ w ) ( ∀ z ) [ ¬ Q ( x , z ) ∨ P ( z , w ) ] (\exist w)(\forall z)[\lnot Q(x,z) \lor P(z, w)] (∃w)(∀z)[¬Q(x,z)∨P(z,w)]
则用任意的常量来取代w
( ∃ w ) ( ∀ z ) [ ¬ Q ( x , z ) ∨ P ( z , A ) ] (\exist w)(\forall z)[\lnot Q(x,z) \lor P(z, A)] (∃w)(∀z)[¬Q(x,z)∨P(z,A)]
实质就是找个已知的东西将存在量词的变量取代掉,在 ∀ \forall ∀辖域内就是Skolem函数,之外就是常量,但是使用的函数不允许重名,同时常量符号也不允许重名。
合取范式就是用合取( ∧ \land ∧)连接,括号内用只能是析取

归结演绎推理
自动定理证明:
一般形式:
F
1
∧
F
2
∧
F
n
⇒
W
F_1 \land F_2 \land F_n \Rightarrow W
F1∧F2∧Fn⇒W
反证法:将证明永真改为证明 F 1 ∧ F 2 ∧ F n ∧ ¬ W F_1 \land F_2 \land F_n \land \lnot W F1∧F2∧Fn∧¬W永假
子句就是仅有析取(
∨
\lor
∨)构成的合适公式
合取范式可定义为子句的合取(
∧
\land
∧)


合适公式
→
合取范式
→
子句集
S
合适公式 \rightarrow 合取范式 \rightarrow 子句集S
合适公式→合取范式→子句集S
其中一个重要的性质:
子句集
S
的不可满足性
↔
合适公式永假
子句集S的不可满足性 \leftrightarrow 合适公式永假
子句集S的不可满足性↔合适公式永假
归结原理

而加入归结式的子句集
S
′
S'
S′与原来子句集在不可满足性上式等价的

对子句集的消解规则:
- 假言推理 P , ¬ P ∨ Q ⇒ Q P, \lnot P \lor Q \Rightarrow Q P,¬P∨Q⇒Q
- 合并 P ∨ Q , ¬ P ∨ Q ⇒ Q P \lor Q, \lnot P \lor Q \Rightarrow Q P∨Q,¬P∨Q⇒Q
- 重言式
P
∨
Q
,
¬
P
∨
¬
Q
⇒
Q
∨
¬
Q
或者
(
P
∨
¬
P
)
P \lor Q, \lnot P \lor \lnot Q \Rightarrow Q \lor \lnot Q 或者(P \lor \lnot P)
P∨Q,¬P∨¬Q⇒Q∨¬Q或者(P∨¬P)
注意并不是空 - 空子句
P
,
¬
P
⇒
N
I
L
P, \lnot P \Rightarrow NIL
P,¬P⇒NIL
只用一个符号是才为空
子句中的文字知识原子命题公式或其取反,不带变量,这样易于判别那些子句对包含互补文字
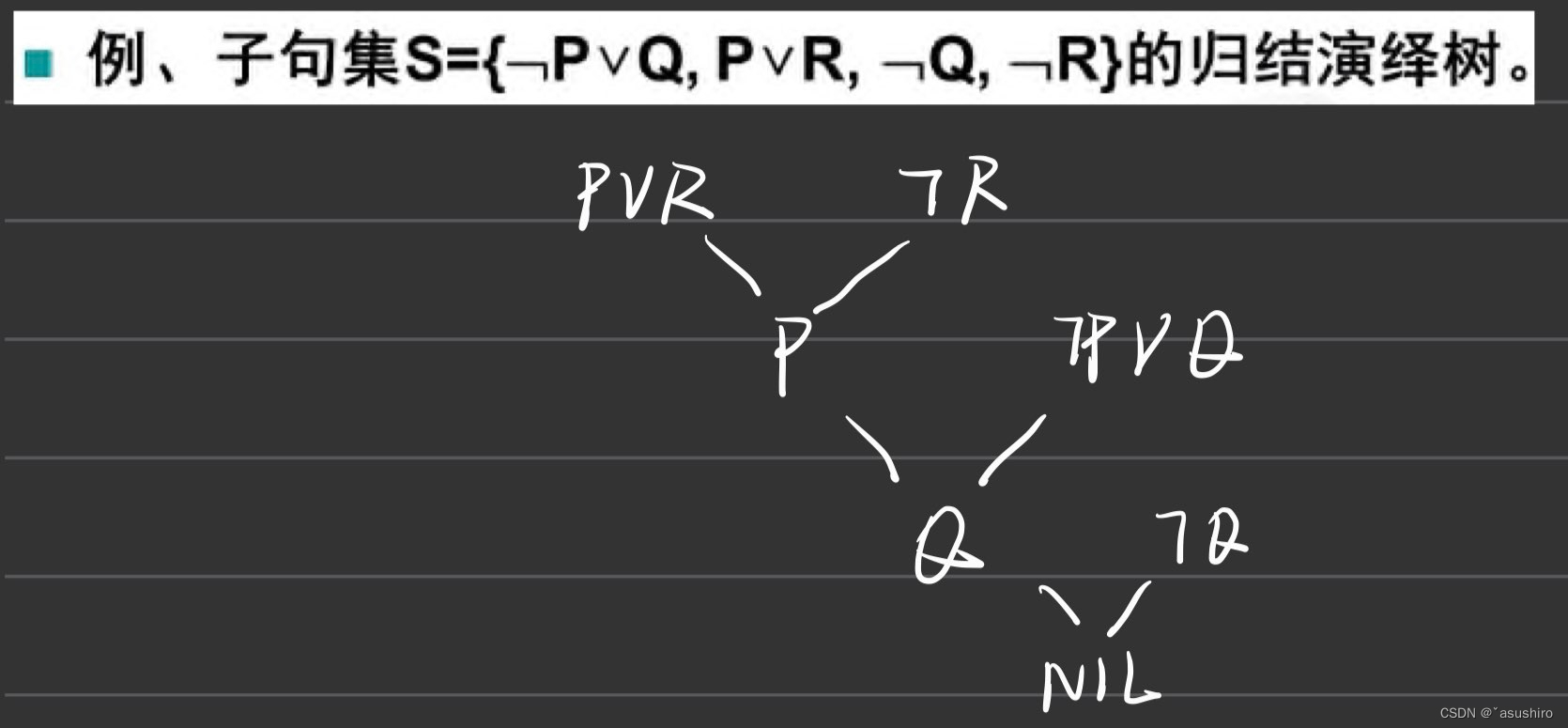
子句中含有变量,不能直接发现和消去互补文字,需要对潜在的互补文字先做变量置换和合一处理。
置换项可以是常量、变量或函数 t / v (置换项后 / 源变量) ,置换就是为了让谓词公式的文字同一确定互补性。



但是如果子句集是永真,可满足的那么归结原理将永无休止的进行下去,得不到任何结果
归结反演
将结论取反与公式集合取,然后将这个
F
∧
¬
W
F \land \lnot W
F∧¬W标准为子句,并合并为子句集S


归结反演也可根据归结树的结果提取有效信息

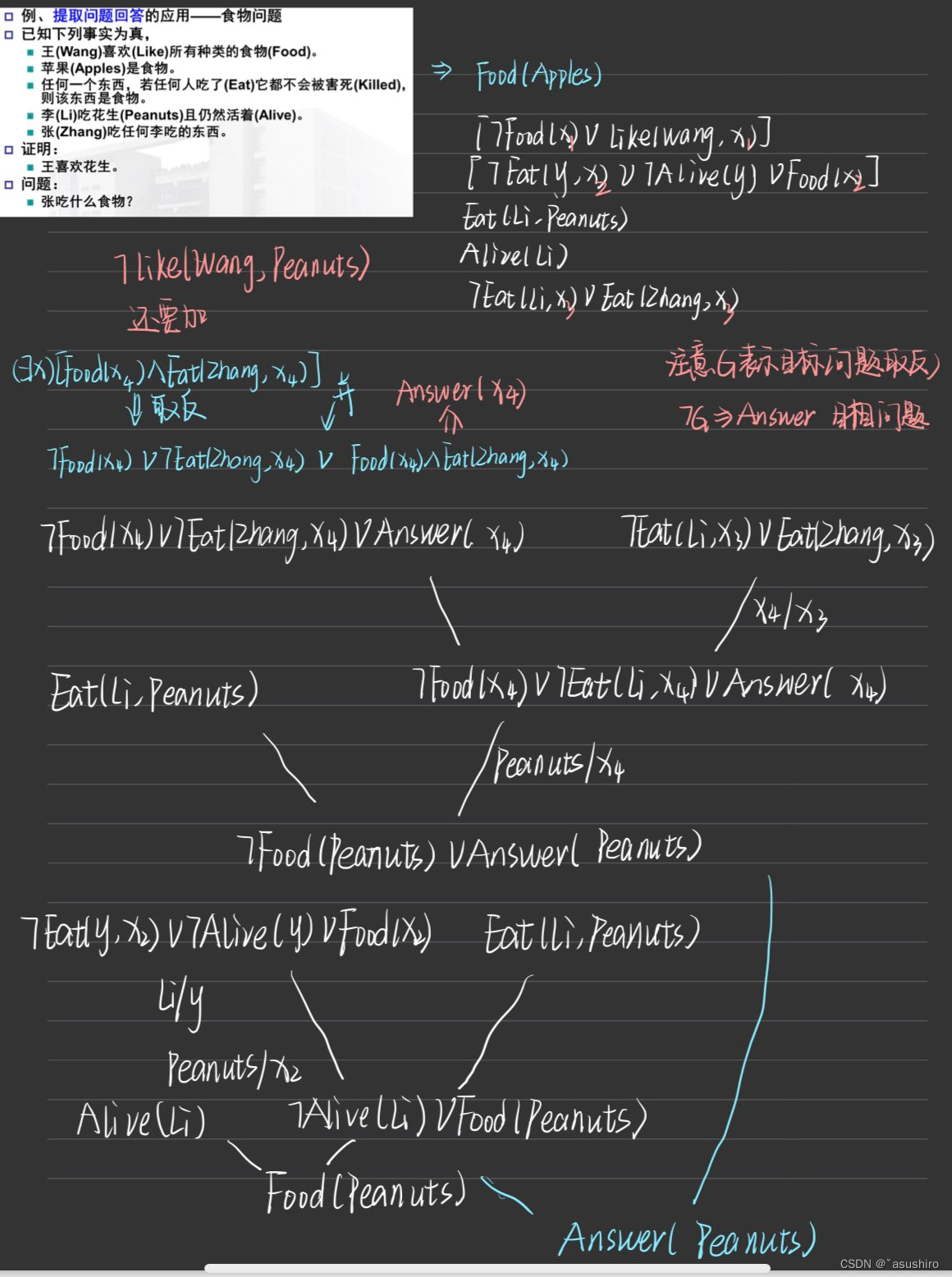
归结反演可实现提取问题回答
回答问题时,目标公式往往受存在量词约束,这是回答提取,就是给出使W(x)为真的x的某个值。
方法就是建立目标子句G(G是要回答问题的取反)的重言式(永真式)
G
∨
¬
G
G \lor \lnot G
G∨¬G,将这个重言式加入归结演绎过程取代原来的G,这时生成的树是修改证明树,此时树根不再是空子句,而是
¬
G
\lnot G
¬G, G被置换项取代,实现问题回答,这个取代的结果就是回答的结果。
但是重言式中的 ¬ G \lnot G ¬G (而这个 ¬ G 就和要回答问题的含义相同 \lnot G就和要回答问题的含义相同 ¬G就和要回答问题的含义相同)并不真正参与归结演绎,只是G中的变量在置换时会跟着置换, 所以为了避免在归结反演的过程中误用 ¬ G \lnot G ¬G就用特殊的符号将它代替掉如 Answer( x 1 , x 2 , . . . , x n x_1, x_2, ..., x_n x1,x2,...,xn),其中 x i x_i xi为 ¬ G \lnot G ¬G中的变量。
特殊情况:
- 目标公式也可能会有更复杂的形式,当目标公示取反后的G中有多个合取时,这是将子句分开分别建立重言式寻求答案。
- 当目标公式中含有全程量词时,取反后G中就有存在量词需要用Skolmn函数,常量消除存在量词。


提升归结效率
为了快速产生空子句有一下策略:
-
宽度优先搜索
会归结出许多无用的子句,既浪费时间又浪费空间,但是当问题有解时能找到最短归结路径,他是一种完备的归结策略。对大问题会组合爆炸,但对小问题是较好的归结策略。 -
支持集策略
要求每次归结都要有目标公式的否定所得到的子句或它们的后裔,完备的归结策略,虽然会限制子句集元素的剧增,但是会增加空子句所在的深度 -
删除策略
在归结过程中把子句集中无用的子句删除掉- 纯文字:如果子句集中不存在与其互补的文字可以将这整个子句删掉
例如 S = { P ∨ Q ∨ R , ¬ Q ∨ R , Q , ¬ R } S = \{ P \lor Q \lor R, \lnot Q \lor R, Q, \lnot R\} S={P∨Q∨R,¬Q∨R,Q,¬R}其中P没有与其互补的可以将 P ∨ Q ∨ R P \lor Q \lor R P∨Q∨R删掉 - 包孕:对于子句C1和C2 如果C1经过置换是C2的子集,就说C1包孕于C2. 将C1删掉对整个子句集的不可满足性没有影响
- 重言式:如果子句中含有重言式就可以删掉重言式。
按照这个规则删除的是完备的。
- 纯文字:如果子句集中不存在与其互补的文字可以将这整个子句删掉
-
单文字子句策略
单文字就是子句中只有一个文字,要求每次参与归结至少有一个是单文字,单文字可以有效减少文字数,所以有较高的归结效率,但是这个策略是不完备的,当子句集是不可满足时,不一定可以归结出空子句。 -
线性输入策略
要求每次参与归结至少应该有一个是初始子句集的子句,可以提高效率,但是是不完备的。
下一篇
未完待续







![洛谷 [AGC032B] Balanced Neighbors](https://img-blog.csdnimg.cn/direct/08fbeb61c68a4662ad4c0915313f2716.png)