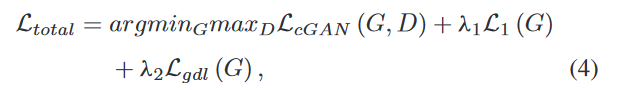抑制过拟合——从梯度的角度看LayerNorm的作用

Normalization的目的
LayerNorm & BatchNorm
可视化分析LayerNorm
- 分析loss
- 分析梯度

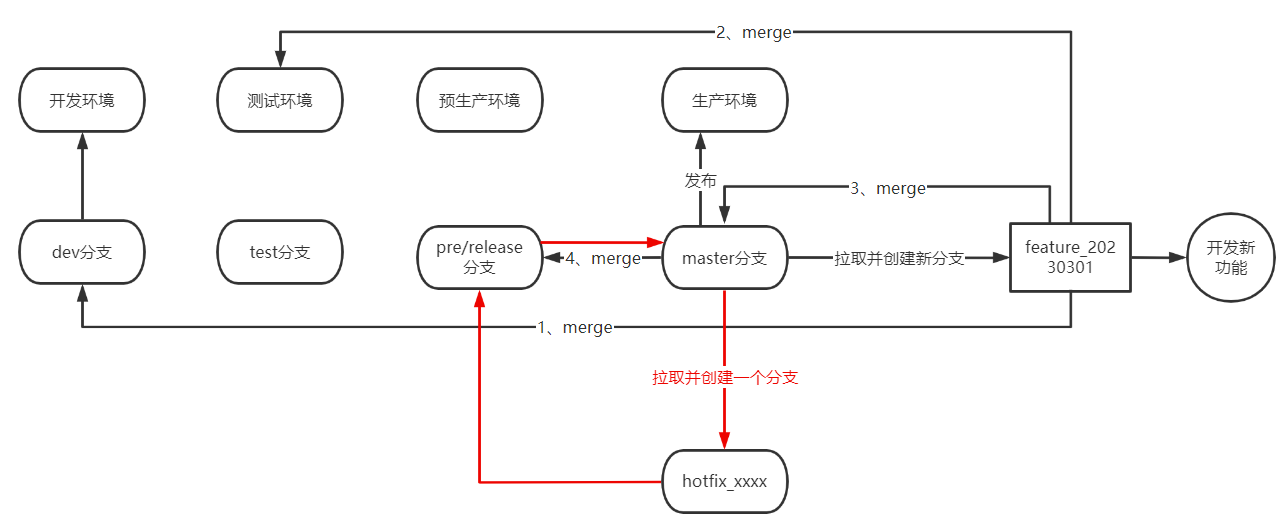
在深入探索transformer模型时，一个不可忽视的组成部分便是LayerNorm，它在模型的优化过程中起着关键作用。相比之下，虽然BatchNorm也广泛应用于各种网络模型中，但在很多情况下LayerNorm表现出更优的效果。然而，对于为何LayerNorm优于BatchNorm，目前学界还没有形成统一的看法。

在这里插入图片描述

本文的重点是探讨LayerNorm在模型训练过程中对梯度变化的影响。通过对这一作用的深入理解，我们可以更加有效地应用LayerNorm，从而提升模型的性能。

Normalization的目的

在使用梯度下降法进行优化的过程中，特别是在深层网络中，输入数据的特征分布会随着网络深度的增加而发生变化。为了维持数据特征分布的稳定性，通常会引入Normalization。这不仅能够使得模型使用更大的学习率，加速模型收敛，同时也有助于防止过拟合，使训练过程更加平稳。

简而言之，Normalization的主要作用是在特征输入激活函数之前进行标准化处理，将数据转换为均值为0、方差为1的分布。这一处理避免了数据落入激活函数的饱和区，从而降低了梯度消失问题的风险。

从更深层次来看，Normalization 通过将数据拉回标准正态分布，提高了网络运算的稳定性。由于神经网络的大部分操作都是矩阵运算，未经处理的向量在经过多次运算后其值可能逐渐增大。因此，为了维持网络的稳定性，定期将数据值拉回到正态分布显得尤为重要。

LayerNorm & BatchNorm

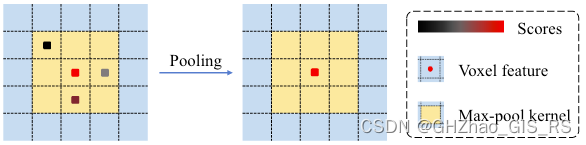
在理解LayerNorm与BatchNorm的不同之处时，一个直观的示意图可以帮助我们更清晰地认识两者的区别。

在这里插入图片描述

假设输入数据的维度为[batch_size, seq_len, emb_dim]。在这种情况下，LayerNorm是针对batch中的单个数据点的[seq_len, emb_dim]维度进行normalization，而BatchNorm则是针对[batch_size, seq_len]维度进行normalization。

考虑到文本任务中文本长度和词嵌入的特性，LayerNorm在处理[seq_len, emb_dim]的normalization时通常会比BatchNorm更有效。

具体来说，BN（Batch Normalization）在保留不同样本之间的大小关系的同时，抹平了不同特征之间的差异。这在依赖于样本间关系的任务中特别有效，例如在计算机视觉领域中对不同图片样本进行分类时。

而LN（Layer Normalization）则是在保留不同特征之间的大小关系的同时，抹平了不同样本之间的差异。这使得LN特别适用于自然语言处理领域的任务，其中一个样本的特征实际上是由不同的词嵌入组成。通过LN，可以有效地保留这些特征间的时序关系。

可视化分析LayerNorm

为了更深入地理解LayerNorm的作用，本文设计了四个实验来观察其对梯度变化的影响。这四个实验的模型结构如下表所示：

模型名称	描述
实验1	Dropout
实验2	Dropout + LayerNorm
实验3	LayerNorm
实验4	None

实验1 Dropout结构如下：

class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linears = nn.Sequential(
            nn.Linear(2, 20),
            nn.Linear(20, 20),
            nn.Dropout(0.1),
            nn.Linear(20, 20),
            nn.Linear(20, 20),
            nn.Linear(20, 1),
        )

    def forward(self, x):
        _ = self.linears(x)
        return _

实验2 Dropout + LayerNorm结构如下：

class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linears = nn.Sequential(
            nn.Linear(2, 20),
            nn.Linear(20, 20),
            nn.Dropout(0.1),
            nn.Linear(20, 20),
            nn.LayerNorm(20),
            nn.Linear(20, 20),
            nn.LayerNorm(20),
            nn.Linear(20, 1),
        )

    def forward(self, x):
        _ = self.linears(x)
        return _

实验3 LayerNorm结构如下：

class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linears = nn.Sequential(
            nn.Linear(2, 20),
            nn.Linear(20, 20),
            nn.Linear(20, 20),
            nn.LayerNorm(20),
            nn.Linear(20, 20),
            nn.LayerNorm(20),
            nn.Linear(20, 1),
        )

    def forward(self, x):
        _ = self.linears(x)
        return _

实验4 None结构如下：

class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linears = nn.Sequential(
            nn.Linear(2, 20),
            nn.Linear(20, 20),
            nn.Linear(20, 20),
            nn.Linear(20, 20),
            nn.Linear(20, 1),
        )

    def forward(self, x):
        _ = self.linears(x)
        return _

训练代码如下：

import torch
from tensorboardX import SummaryWriter
from torch import optim, nn
import time


class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linears = nn.Sequential(
            nn.Linear(2, 20),

            nn.Linear(20, 20),
            # nn.Dropout(0.1),

            nn.Linear(20, 20),
            # nn.LayerNorm(20),

            nn.Linear(20, 20),
            # nn.LayerNorm(20),

            nn.Linear(20, 1),
        )

    def forward(self, x):
        _ = self.linears(x)
        return _

lr = 0.01
iteration = 1000


x1 = torch.arange(-10, 10).float()
x2 = torch.arange(0, 20).float()
x = torch.cat((x1.unsqueeze(1), x2.unsqueeze(1)), dim=1)
y = 2*x1 - x2**2 + 1

model = Model()
optimizer = optim.Adam(model.parameters(), lr=lr, weight_decay=0.01)
loss_function = torch.nn.MSELoss()

start_time = time.time()
writer = SummaryWriter(comment='_层归一化')

for iter in range(iteration):
    y_pred = model(x)
    loss = loss_function(y, y_pred.squeeze())
    loss.backward()

    for name, layer in model.named_parameters():
        writer.add_histogram(name + '_grad', layer.grad, iter)
        writer.add_histogram(name + '_data', layer, iter)
    writer.add_scalar('loss', loss, iter)

    optimizer.step()
    optimizer.zero_grad()

    if iter % 50 == 0:
        print("iter: ", iter)

print("Time: ", time.time() - start_time)

这里我们使用 TensorBoardX 进行结果的可视化展示。

分析loss

实验结果如下所示：

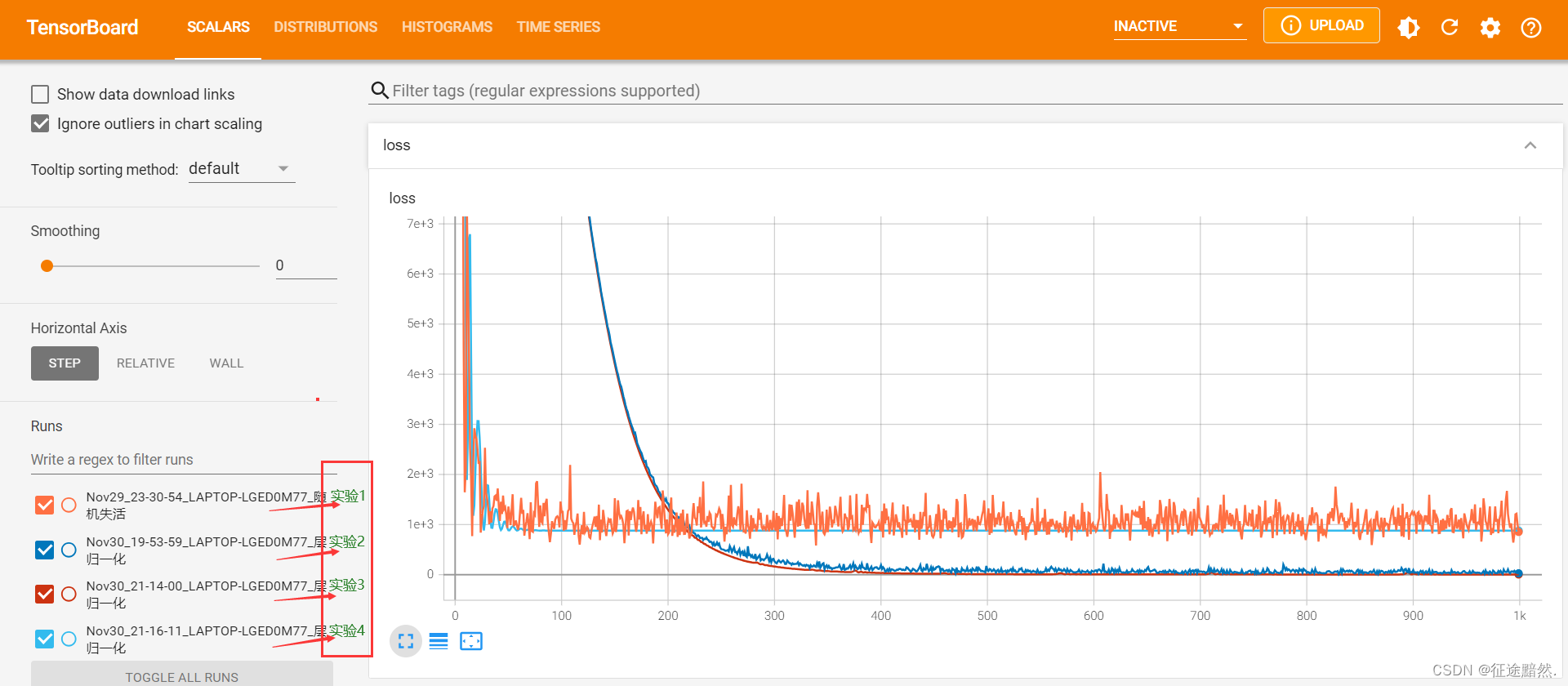
在这里插入图片描述

可以看到，加入了LayerNorm的实验2和3的最终loss明显低于没有使用LayerNorm的实验1和4。

我们认为LayerNorm能够帮助降低模型损失的原因主要有以下几点：
1、稳定化学习过程： 层归一化通过对每个样本的特征进行独立归一化，有效减少了不同层输出分布的变化（也称为内部协变量偏移），从而有助于稳定网络的学习过程，使网络更容易学习。
2、加速收敛： 层归一化通过减少不同训练批次间的系统差异，可以显著加速神经网络的收敛速度，使网络能够更快地达到较低的损失值。

通过对实验1、2和实验3、4的比较，我们发现加入了Dropout的实验1和2其损失值波动较大，而没有使用Dropout的实验3和4则显示出更为平滑的收敛过程。

分析梯度

实验结果如下所示：

在这里插入图片描述
通过深入分析这些实验结果，我们可以更好地理解LayerNorm在控制梯度分布方面的作用。让我们逐一探讨每个实验的结果和它们所揭示的洞见。

实验4（无任何正则化）：这个实验没有应用Dropout或LayerNorm。其结果显示，梯度在训练的初期阶段迅速稳定下来，但分布非常集中。这种过于集中的分布通常是过拟合的迹象。过拟合意味着模型可能在训练数据上表现出色，但在未见过的数据上则表现不佳。这种现象在深度学习中非常常见，尤其是在没有足够的正则化措施时。

实验1（仅使用Dropout）：相比于实验4，实验1引入了Dropout层。Dropout是一种有效的正则化技术，它通过在训练过程中随机“关闭”一部分神经元来减少模型对特定训练样本的依赖。这导致了更加“杂乱无章”的梯度分布，这实际上是好事，因为它表明模型正在学习更多样化的特征，而不是仅仅依赖于特定的模式或数据点。

实验2（Dropout + LayerNorm）：这个实验在Dropout的基础上增加了LayerNorm。LayerNorm通过独立地标准化每个样本的特征来减少不同层之间的输出分布的变化，有助于进一步稳定训练过程。从实验结果可以看出，实验2的梯度分布比实验1更加集中和均匀，这表明结合Dropout和LayerNorm可以提供更好的正则化效果，使得模型能够更有效地学习并防止过拟合。

实验3（仅使用LayerNorm）：最后，实验3专注于单独使用LayerNorm。这个实验的结果介于实验4和实验1之间。它没有实验4那样的过拟合梯度分布，也没有实验1中Dropout导致的极端波动。这表明LayerNorm自身是一个有效的正则化方法，能够平衡模型的学习过程，即使在没有Dropout的情况下也能防止过拟合。

LayerNorm在维持梯度分布稳定性和提高模型泛化能力方面的重要作用。