文章目录
- 一、数值积分法
- 1. 一般步骤
- 2. 数值方法
- 二、欧拉方法(Euler Method)
- 1. 向前欧拉法(前向欧拉法)
- 2. 向后欧拉法(后向欧拉法)
- a. 基本理论
- b. 算法实现
常微分方程初值问题的数值积分法是一种通过数值方法求解给定初始条件下的常微分方程(Ordinary Differential Equations, ODEs)的问题。
一、数值积分法
1. 一般步骤
-
确定微分方程:
- 给定微分方程组 y ′ ( x ) = f ( x , y ( x ) ) y'(x) = f(x, y(x)) y′(x)=f(x,y(x))
-
确定初始条件:
- 初值问题包含一个初始条件 y ( a ) = y 0 y(a) = y_0 y(a)=y0,其中 a a a 是定义域的起始点, y 0 y_0 y0 是初始值。
-
选择数值方法:
- 选择适当的数值方法来近似解(需要考虑精度、稳定性和计算效率),常见的数值方法包括欧拉方法、改进的欧拉方法、Runge-Kutta 方法等。
-
离散化定义域:
- 将定义域 [ a , b ] [a, b] [a,b] 分割为若干小步,即选择合适的步长 h h h。通常,较小的步长能够提高数值解的精度,但也增加计算成本。
-
数值迭代:
- 使用选定的数值方法进行迭代计算:根据选择的方法,计算下一个点的函数值,并更新解。
-
判断停止条件:
- 判断是否达到满足指定精度的近似解:可以使用某种误差估计方法,例如控制局部截断误差或全局误差。
-
输出结果:
- 最终得到在给定定义域上满足初值问题的近似解。
2. 数值方法
-
欧拉方法(Euler Method):
- 基本思想:根据微分方程的定义,使用离散步长逼近导数,进而逼近下一个点的函数值。
- 公式:
y
n
+
1
=
y
n
+
h
f
(
t
n
,
y
n
)
y_{n+1} = y_n + h f(t_n, y_n)
yn+1=yn+hf(tn,yn)
其中, y n y_n yn是第 n n n 步的函数值, h h h是步长, f ( t n , y n ) f(t_n, y_n) f(tn,yn) 是在点 ( t n , y n ) (t_n, y_n) (tn,yn) 处的导数。
-
改进的欧拉方法(Improved Euler Method 或梯形法 Trapezoidal Rule):
- 基本思想:使用两次近似来提高精度,首先使用欧拉方法计算中间点,然后用该点的导数估计值来计算下一个点。
- 公式: y n + 1 = y n + h 2 [ f ( t n , y n ) + f ( t n + 1 , y n + h f ( t n , y n ) ) ] y_{n+1} = y_n + \frac{h}{2} [f(t_n, y_n) + f(t_{n+1}, y_n + hf(t_n, y_n))] yn+1=yn+2h[f(tn,yn)+f(tn+1,yn+hf(tn,yn))]
-
Runge-Kutta 方法:
- 基本思想:通过多个阶段的计算来提高精度。其中最常见的是四阶 Runge-Kutta 方法。
- 公式:
k 1 = h f ( t n , y n ) k_1 = hf(t_n, y_n) k1=hf(tn,yn) k 2 = h f ( t n + h 2 , y n + k 1 2 ) k_2 = hf(t_n + \frac{h}{2}, y_n + \frac{k_1}{2}) k2=hf(tn+2h,yn+2k1) k 3 = h f ( t n + h 2 , y n + k 2 2 ) k_3 = hf(t_n + \frac{h}{2}, y_n + \frac{k_2}{2}) k3=hf(tn+2h,yn+2k2) k 4 = h f ( t n + h , y n + k 3 ) k_4 = hf(t_n + h, y_n + k_3) k4=hf(tn+h,yn+k3) y n + 1 = y n + 1 6 ( k 1 + 2 k 2 + 2 k 3 + k 4 ) y_{n+1} = y_n + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4) yn+1=yn+61(k1+2k2+2k3+k4)
这些方法中,步长 h h h 是一个关键参数,它决定了离散化的程度,选择合适的步长对于数值解的准确性和稳定性非常重要。
二、欧拉方法(Euler Method)
1. 向前欧拉法(前向欧拉法)
【计算方法与科学建模】常微分方程初值问题的数值积分法:欧拉方法(向前Euler及其python实现)
- 向前差商近似微商:
- 在节点 X n X_n Xn 处,通过向前差商 y ( X n + 1 ) − y ( X n ) h \frac{y(X_{n+1}) - y(X_n)}{h} hy(Xn+1)−y(Xn) 近似替代微分方程 y ′ ( x ) = f ( x , y ( x ) ) y'(x) = f(x, y(x)) y′(x)=f(x,y(x)) 中的导数项,得到 y ′ ( X n ) ≈ y ( X n + 1 ) − y ( X n ) h = f ( X n , y ( X n ) ) y'(X_n) \approx \frac{y(X_{n+1}) - y(X_n)}{h} = f(X_n, y(X_n)) y′(Xn)≈hy(Xn+1)−y(Xn)=f(Xn,y(Xn))
- 这个近似通过将差商等于导数的思想,将微分方程转化为递推关系式。
- 递推公式:
- 将上述近似公式改为等式,得到递推公式 y n + 1 = y n + h f ( X n , y n ) y_{n+1} = y_n + hf(X_n, y_n) yn+1=yn+hf(Xn,yn)
- 这个公式是 Euler 方法的核心,通过这个公式可以逐步计算得到近似解的数值。
2. 向后欧拉法(后向欧拉法)
a. 基本理论
向后 Euler 方法的核心思想是从微分方程的 y ′ ( X n + 1 ) = f ( x n + 1 , y ( X n + 1 ) ) y'(X_{n+1}) = f(x_{n+1}, y(X_{n+1})) y′(Xn+1)=f(xn+1,y(Xn+1)) 出发,使用向后差商 y ( X n + 1 ) − y ( X n ) h \frac{y(X_{n+1}) - y(X_n)}{h} hy(Xn+1)−y(Xn) 近似微商 y ′ ( X n + 1 ) y'(X_{n+1}) y′(Xn+1),然后通过这个近似来得到递推公式。具体而言,递推公式为:
y n + 1 = y n + h f ( X n + 1 , y n + 1 ) , n = 0 , 1 , … y_{n+1} = y_n + hf(X_{n+1}, y_{n+1}), \quad n = 0, 1, \ldots \ yn+1=yn+hf(Xn+1,yn+1),n=0,1,…
这里, y n + 1 y_{n+1} yn+1 是在 X n + 1 X_{n+1} Xn+1 处的近似解, h h h 是步长。
对比向前 Euler 方法和向后 Euler 方法,可以注意到两者的关键区别:
-
显式 vs. 隐式:
- 向前 Euler 方法给出了一个显式的递推公式,可以直接计算 y n + 1 y_{n+1} yn+1。
- 向后 Euler 方法给出了一个隐式的递推公式,其中 y n + 1 y_{n+1} yn+1出现在方程的右侧,需要通过求解非线性方程来获得。
-
求解方式:
- 向前 Euler 方法的解可以通过简单的迭代计算得到。
- 向后 Euler 方法的解需要通过迭代求解非线性方程,通常,可以使用迭代法,如牛顿迭代法,来逐步逼近方程的解。
-
具体的迭代过程:
-
初始值:使用向前 Euler 公式给出一个初值,例如 y n + 1 ( 0 ) = y n + h f ( x n + 1 , y n ) y_{n+1}^{(0)} = y_n + hf(x_{n+1}, y_n) yn+1(0)=yn+hf(xn+1,yn),其中 y n + 1 ( 0 ) y_{n+1}^{(0)} yn+1(0) 是迭代的初值。
-
迭代公式:使用迭代公式 y n + 1 ( k + 1 ) = y n + h f ( x n + 1 , y n + 1 ( k ) ) , k = 0 , 1 , … y_{n+1}^{(k+1)} = y_n + hf(x_{n+1}, y_{n+1}^{(k)}), \quad k = 0, 1, \ldots yn+1(k+1)=yn+hf(xn+1,yn+1(k)),k=0,1,…计算 y n + 1 y_{n+1} yn+1 的逼近值。
-
重复迭代,直到满足收敛条件,得到 y n + 1 y_{n+1} yn+1 的近似解。
-
向后 Euler 方法在处理某些问题(例如刚性问题)时可能更为稳定,但由于涉及隐式方程的求解,其计算成本可能较高。
b. 算法实现
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve
def forward_euler(f, y0, a, b, h):
"""
使用向前欧拉法求解一阶常微分方程初值问题
Parameters:
- f: 函数,表示微分方程的右侧项,形式为 f(x, y)
- y0: 初始条件,表示在 x=a 处的函数值
- a: 区间起点
- b: 区间终点
- h: 步长
Returns:
- x_values: 区间 [a, b] 上的离散节点
- y_values: 对应节点上的函数值的近似解
"""
num_steps = int((b - a) / h) + 1 # 计算步数
x_values = np.linspace(a, b, num_steps) # 生成离散节点
y_values = np.zeros(num_steps) # 初始化结果数组
y_values[0] = y0 # 设置初始条件
# 使用向前欧拉法进行逐步迭代
for i in range(1, num_steps):
x = x_values[i - 1]
y = y_values[i - 1]
y_values[i] = y + h * f(x, y)
return x_values, y_values
def backward_euler(f, y0, a, b, h):
"""
使用向后欧拉法求解一阶常微分方程初值问题
Parameters:
- f: 函数,表示微分方程的右侧项,形式为 f(x, y)
- y0: 初始条件,表示在 x=a 处的函数值
- a: 区间起点
- b: 区间终点
- h: 步长
Returns:
- x_values: 区间 [a, b] 上的离散节点
- y_values: 对应节点上的函数值的近似解
"""
num_steps = int((b - a) / h) + 1 # 计算步数
x_values = np.linspace(a, b, num_steps) # 生成离散节点
y_values = np.zeros(num_steps) # 初始化结果数组
y_values[0] = y0 # 设置初始条件
# 使用向后欧拉法进行逐步迭代
for i in range(1, num_steps):
x = x_values[i]
# 定义非线性方程
equation = lambda y_next: y_next - y_values[i - 1] - h * f(x, y_next)
# 利用 fsolve 求解非线性方程,得到 y_values[i]
y_values[i] = fsolve(equation, y_values[i - 1])[0]
return x_values, y_values
# 示例:求解 y' = y -2x/y,初始条件 y(0) = 1 在区间 [0, 1] 上的近似解
def example_function(x, y):
return y - 2 * x / y
a, b = 0, 1 # 区间 [a, b]
y0 = 1 # 初始条件 y(0) = 1
h = 0.05 # 步长
x_values0, y_values0 = forward_euler(example_function, y0, a, b, h)
x_values, y_values = backward_euler(example_function, y0, a, b, h)
# 绘制结果
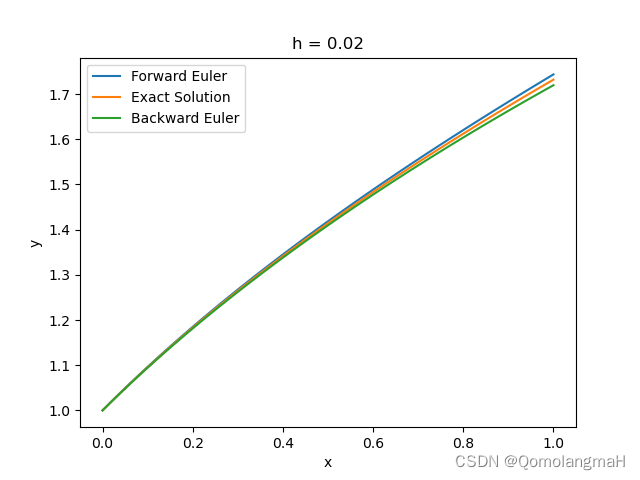
plt.plot(x_values0, y_values0, label='Forward Euler')
plt.plot(x_values, np.sqrt(1 + 2 * x_values), label='Exact Solution')
plt.plot(x_values, y_values, label='Backward Euler')
plt.title('h = {}'.format(h))
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
-
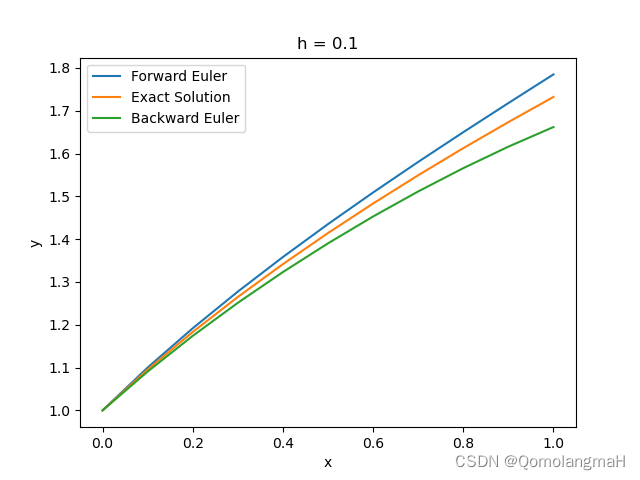
h = 0.1
-
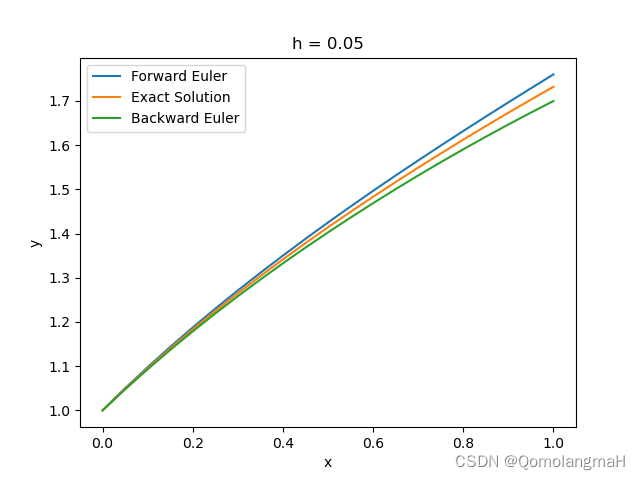
h = 0.05
-
h = 0.02