数据结构：哈希表讲解

哈希表

- 1.哈希概念
- 2.通过关键码确定存储位置
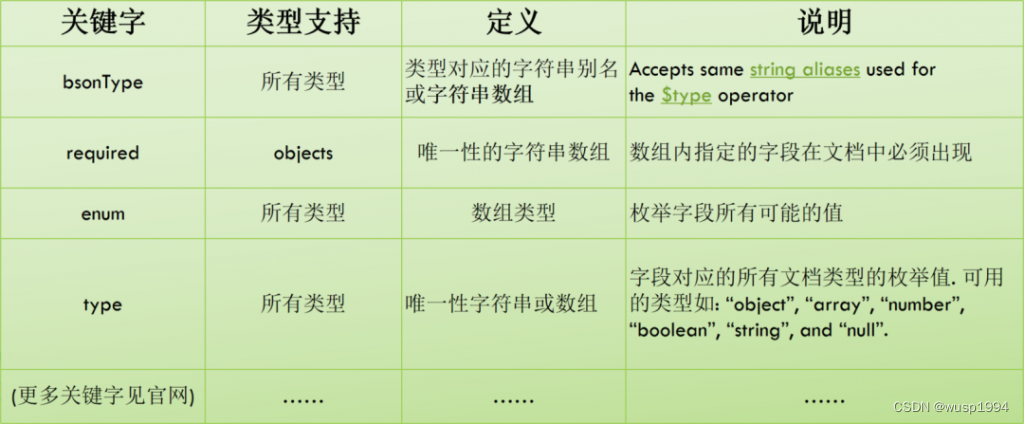
- - 2.1哈希方法
  - 2.2直接定址法
  - 2.3除留余数法
- 3.哈希冲突概念
- 4.解决哈希冲突
- - 4.1闭散列
  - - 4.1.1概念
    - 4.1.2哈希表扩容
    - 4.1.3存储位置的状态
    - 4.1.4关于键值类型
    - 4.1.5代码实现
  - 4.2开散列
  - - 4.2.1概念
    - 4.2.2哈希表扩容
    - 4.2.3代码实现
  - 4.3开闭散列的对比

1.哈希概念

哈希：一种映射思想，也叫散列。即关键字和另一个值建立一个关联关系。注意这里指的关联关系是多样的，比如给你关键字，你可以通过映射关系确定该值在不在或者获得其它信息，不一定要存储另一个值。

哈希表：也叫散列表，体现了哈希思想。即关键字和存储位置建立关联关系，这里的关系是比较具体的。通常是哈希表中存储键值对，通过key来找到键值对的存储位置，从而进行对value的快速查找。

哈希表主要用来提高搜索效率，这里对比一下：

顺序表：时间复杂度为O(N)，暴力查找。
平衡搜索树：时间复杂度为O( $log_2 n$ )，效率稳定，也比较快。
哈希表：平均时间复杂度为O(1)，平均常数级别查找（这里是平均复杂度，哈希表存在极端情况退化，后面会分析）。

2.通过关键码确定存储位置

2.1哈希方法

我们通常会对关键码进行转化来确定存储位置，这个转化的方式即为哈希方法，哈希方法中使用的转化函数称为哈希函数（方法是一种指导，哈希函数设计可以存在差别）。

⭐哈希函数关系哈希表中的两个常用操作：

插入元素
根据待插入元素的关键码，以此函数计算出该元素的存储位置并按此位置进行存放
查找元素
对元素的关键码进行同样的计算，把求得的函数值当做元素的存储位置，在结构中按此位置取元素比较，若关键码相等，则搜索成功

本文主要讲两种哈希方法：

直接地址法
除留余数法

2.2直接定址法

该方法的哈希函数：hashi = a * key + b(其中a、b为自定义的常数，a != 0)。
概念：值和位置建立唯一关系。

适用场景：关键码比较集中的情况
(比如统计字母出现次数，关键码为字母，都集中在一段小区间)。

缺点：对于关键码分散的情况，会造成严重的空间浪费。
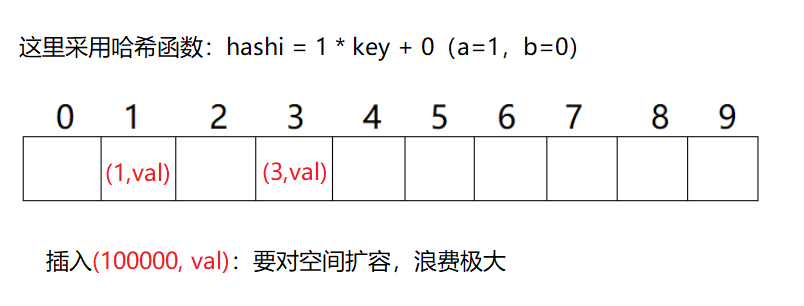
在这里插入图片描述

2.3除留余数法

该方法的哈希函数：hashi = key % len(其中hashi表示存储下标，key表示关键码，len表示哈希表的长度)。
概念：通过对关键码的转化，让存储位置落在哈希表现有空间中。

适用场景：关键码集中或者分散都可以用这个方法，通过哈希函数计算后存储位置都是落在一段固定的空间内。

缺点：不同的关键码通过哈希函数计算出的存储位置可能相同，从而引起冲突。这个现象称为哈希冲突，解决哈希冲突是后面的核心。

在这里插入图片描述

3.哈希冲突概念

概念：不同关键字通过相同哈希函数计算出相同的哈希地址，该种现象称为哈希冲突或哈希碰撞。

哈希冲突的发生与哈希函数有关，哈希函数设计的越合理哈希冲突就越少，这里介绍一下几种哈希方法：

直接定址法（常用），前面分析过，不讲。
除留余数法（常用），前面分析了，不讲。
平方取中法（了解）
假设关键字为1234，对它平方就是1522756，抽取中间的3位227作为哈希地址；
再比如关键字为4321，对它平方就是18671041，抽取中间的3位671(或710)作为哈希地址；
平方取中法比较适合：不知道关键字的分布，而位数又不是很大的情况
折叠法（了解）
折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些)，然后将这几部分叠加求和，并按散列表表长，取后几位作为散列地址。
折叠法适合事先不需要知道关键字的分布，适合关键字位数比较多的情况
随机数法（了解）
选择一个随机函数，取关键字的随机函数值为它的哈希地址，即H(key) = random(key),其中random为随机数函数。
通常应用于关键字长度不等时采用此法

小结：

直接定址法不存在哈希冲突，但适用场景比较局限。
其它几种方法都存在哈希冲突的可能，以除留余数法为例，适用场景更加广泛。本文采用的哈希方法是除留余数法。

4.解决哈希冲突

解决哈希冲突两种常见的方法是：闭散列和开散列

4.1闭散列

4.1.1概念

闭散列：又称开放定址法，即当前位置被占用(哈希冲突)，在开放空间内按某种规则，找一个没被占用的位置存储。
至于寻找未被占用位置的方法，这里讲两种：

线性探测
从发生冲突的位置开始，依次向后探测，直到寻找到下一个空位置为止。
即hashi = hashi + i（i >= 0），重复这个过程。
二次探测
探测的公式变化了而已。
即hashi = hashi + i ^ 2，重复这个过程直到寻找到空位置。

其它细节：

当探测过程中hashi超过了哈希表长度n，要进行一次取余来修正下标，即hashi = hashi % n。不用担心哈希表中找不到空位置，后面会对哈希表扩容。

4.1.2哈希表扩容

负载因子：即 _n / _table.size()，前者为插入的元素个数，后者为哈希表的空间大小。为了减少探测的寻找次数，我们一般会控制负载因子在0.7以下，超过0.7进行扩容。

哈希表扩容的要点：
不能直接申请空间后拷贝，因为我们原先确定存储位置依据 hashi = hashi % len(len为哈希表长度)，现在len发生了变化，值与存储位置的映射已经发生变化，需要重新建立映射。
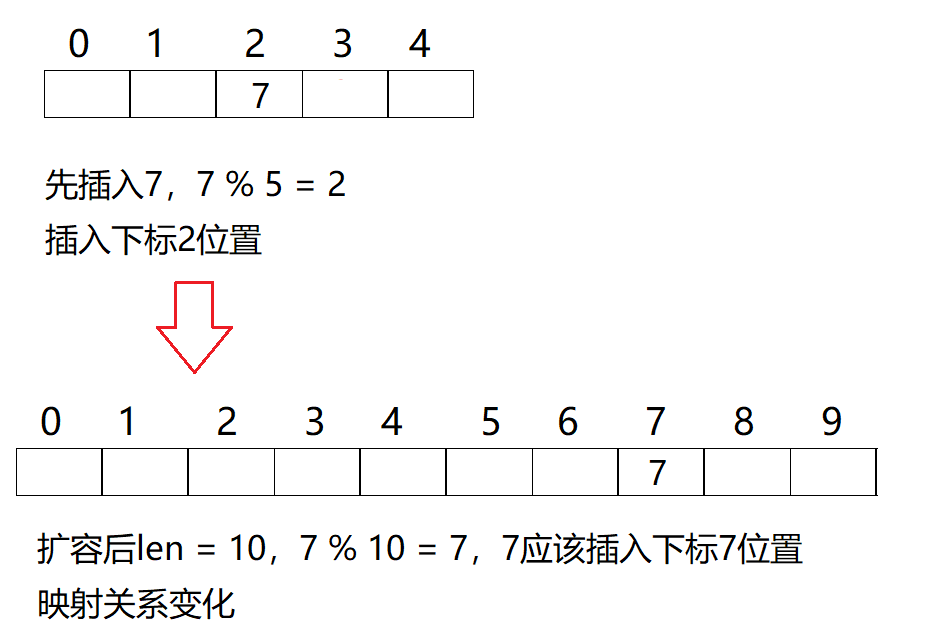
在这里插入图片描述

⭐哈希表扩容的本质：
当冲突较多的时候，扩容重新建立映射可以有效的减少冲突，因此哈希表查找效率退化的情况是非常少见的。
在这里插入图片描述

4.1.3存储位置的状态

表示存储位置的状态在这里是很用必要的，因为插入的过程中不能覆盖别人，要判断当前位置是否冲突，就有必要知道当前位置的状态，当然还有别的原因，后面细讲。

这里引入三种状态：

EMPTY，表示该位置为空。
EXIST，表示该位置被占用了。
DELETE，表示该位置原来用数据，现在被删除了。
删除的时候只要改变对应状态即可，不需要真的删除。

这里让状态和键值对组成一个结构体：

enum Status  //对应位置的状态
{
	EMPTY,
	EXIST,
	DELETE
};

template<class K, class V>  //哈希表中每个位置存储的元素，初始状态默认为空
struct HashData
{
	pair<K, V> _kv;
	Status _s = EMPTY;
};

每个状态的意义(这个比较难理解)：

EMPTY和EXIST比较简单，就是标识当前位置是否被占用。
至于DELETE状态，主要服务于查找。
对于查找，我们也是利用key值转化出存储位置信息，假设插入x时发生了哈希冲突，我们往后找就有下面三种情况：
（1）当前位置位为EXIST，但不是要查找的值，存储位置可能在后面，继续找。
（2）当前位置为DELETE，存储位置可能在后面，继续找。
（原来冲突的值被删除了而已，x可能在后面未被删除）
（3）当前值为EMPTY，不必向后找，可以确定x不存在。
（这里要么x被删除了，要么x没插入过，不然x是可以插入这里的)
如果不设置DELETE状态，查找的时候只能遍历一次哈希表，时间复杂为O(N)，哈希表就没有意义了。

4.1.4关于键值类型

实际中键值不一定是数值类型，可能是不同类型，典型的代表就是字符串。所以一般都会设计一个模板参数，用来转化非数值类型为整形，C++这里采用的是仿函数。这样设计非常灵活，使用者可以依据实际需求自己设计仿函数。

代码：

template < class Key,                                    // unordered_map::key_type
	class T,                                      // unordered_map::mapped_type
	class Hash = hash<Key>,                       // unordered_map::hasher
	class Pred = equal_to<Key>,                   // unordered_map::key_equal
	class Alloc = allocator< pair<const Key, T> >  // unordered_map::allocator_type
> class unordered_map;
//unordered_map的Hash参数即为这里所讲的仿函数类型

//这个是默认的，只要能转化为整形就可以用这个
template<class T>
struct HashFunc
{
	size_t operator()(const T& key)
	{
		return (size_t)key;
	}
};

//因为字符串做键值非常常见，库里面也特化了一份
//字符串哈希算法这里不展开讲，我这里采用的是BKDR算法
template<>
struct HashFunc<string>
{
	size_t operator()(const string& key)
	{
		size_t hashi = 0;
		for (auto ch : key)
		{
			hashi = hashi * 31 + ch;
		}
		return hashi;
	}
};

4.1.5代码实现

理解前面后代码比较简单，我加了注释应该可以看懂。

//这个是默认的，只要能转化为整形就可以用这个
template<class T>
struct HashFunc
{
	size_t operator()(const T& key)
	{
		return (size_t)key;
	}
};

//因为字符串做键值非常常见，库里面也特化了一份
//字符串哈希算法这里不展开讲，我这里采用的是BKDR算法
template<>
struct HashFunc<string>
{
	size_t operator()(const string& key)
	{
		size_t hashi = 0;
		for (auto ch : key)
		{
			hashi = hashi * 31 + ch;
		}
		return hashi;
	}
};

// 闭散列
namespace closed_address
{
	enum Status  //对应位置的状态
	{
		EMPTY,
		EXIST,
		DELETE
	};

	template<class K, class V>  //哈希表中每个位置存储的元素，初始状态默认为空
	struct HashData
	{
		pair<K, V> _kv;
		Status _s = EMPTY;
	};

	template<class K, class V, class Hash = HashFunc<K>>
	class HashTable
	{
	public:
		HashTable()
		{
			//初始默认开10个空间
			_tables.resize(10);
		}

		//  插入
		bool Insert(const pair<K, V>& kv)
		{
			if (Find(kv.first))  //已经存在不能插入，一个键值对占一个位置
			{
				return false;
			}
			Hash hf;   //用来转化非数值类型为整数类型

			//检查是否需要扩容
			if ((double)_n / _tables.size() >= 0.7)
			{
				// 开一个新表，复用insert重新建立映射
				size_t newsize = _tables.size() * 2;
				HashTable<K, V> newHT;
				newHT._tables.resize(newsize);
				//遍历旧表
				for (size_t i = 0; i < _tables.size(); i++)
				{
					if (_tables[i]._s == EXIST)
					{
						newHT.Insert(_tables[i]._kv);
					}
				}
				//交换两个表
				newHT._tables.swap(_tables);
			}

			size_t hashi = hf(kv.first) % _tables.size();
			//线性探测寻找空位置
			while (_tables[hashi]._s == EXIST)
			{
				hashi++;
				//超出哈希表长度要进行修正
				hashi %= _tables.size();
			}
			// 插入
			_tables[hashi]._kv = kv;
			_tables[hashi]._s = EXIST;
			_n++;  //更新插入个数
			return true;
		}

		///  查找
		HashData<K, V>* Find(const K& key)
		{
			Hash hf;
			size_t hashi = hf(key) % _tables.size();
			while (_tables[hashi]._s != EMPTY)  //走到空位置说明该值不在
			{
				// 存在并且键值为key代表找到了，返回结构体指针
				if (_tables[hashi]._kv.first == key && _tables[hashi]._s == EXIST)
				{
					return &_tables[hashi];
				}
				//继续往后找
				hashi++;
				//超出哈希表长度要进行修正
				hashi %= _tables.size();  
			}
			return nullptr;
		}

		// 删除
		bool Erase(const K& key)
		{
			// 查询非空表示找到了
			HashData<K, V>* ret = Find(key);
			if (ret)
			{
				// 修改对应位置状态并加一插入个数即可
				ret->_s = DELETE;
				_n--;
				return true;
			}
			else
			{
				return false;
			}
		}

		//后面的接口不是很重要
		size_t Size()const
		{
			return _n;
		}

		bool Empty() const
		{
			return _n == 0;
		}

		void Swap(HashTable<K, V>& ht)
		{
			swap(_n, ht._n);
			_tables.swap(ht._n);
		}

	private:
		vector<HashData<K, V>> _tables;
		size_t _n = 0;
	};
}

4.2开散列

4.2.1概念

开散列：又称拉链法/哈希桶，即发生冲突时，采用挂链表的形式内部消化，即冲突的元素放在同一链表中，不影响其它位置。

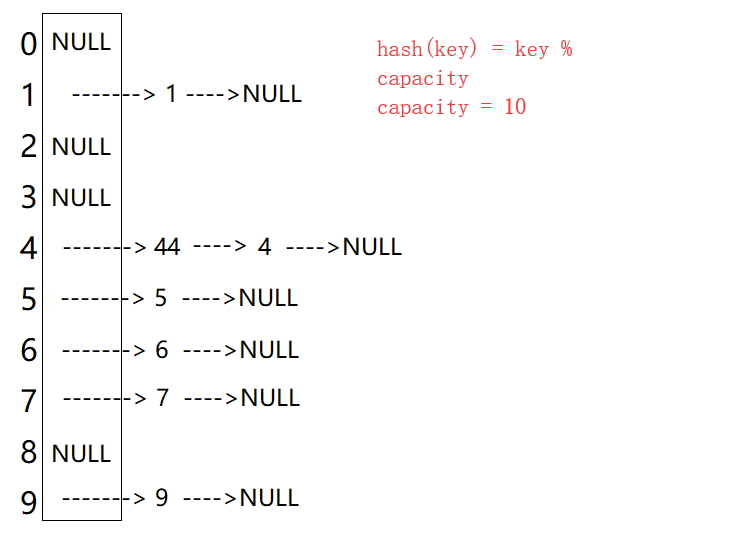
在这里插入图片描述

节点定义：

template<class K, class V>
struct HashNode
{
	HashNode* _next;
	pair<K, V> _kv;

	HashNode(const pair<K, V>& kv)
		:_kv(kv)
		, _next(nullptr)
	{}
};

4.2.2哈希表扩容

开散列扩容：

和前面一样，扩容会改变原来的映射关系，需要重新建立映射。
第一种做法是开新表，复用insert。这样比较简单但消耗比较大，因为需要重新申请节点空间并初始化。
第二种做法是开新表，计算每个节点的新存储位置，直接把节点拿下来插入到新表即可，不必重新开空间。

插入的代码：

bool Insert(const pair<K, V>& kv)
{
	if (Find(kv.first))  //原来已经存在不能插入
		return false;

	Hash hf;  //用来转化非数值类型为整形
	
	//对于开散列扩容
	if (_n == _tables.size())
	{
		vector<Node*> newTables;
		newTables.resize(_tables.size() * 2, nullptr);
		// 遍历旧表
		for (size_t i = 0; i < _tables.size(); i++)
		{
			Node* cur = _tables[i];
			while (cur)
			{
				//先记录下一个节点，防止断掉
				Node* next = cur->_next;

				// 挪动到映射的新表（头插）
				size_t hashi = hf(cur->_kv.first) % newTables.size();
				cur->_next = newTables[hashi];
				newTables[hashi] = cur;

				cur = next;
			}

			_tables[i] = nullptr;
		}

		_tables.swap(newTables);
	}

	size_t hashi = hf(kv.first) % _tables.size();
	Node* newnode = new Node(kv);

	// 新节点头插即可
	newnode->_next = _tables[hashi];
	_tables[hashi] = newnode;
	++_n;

	return true;
}

4.2.3代码实现

//这个是默认的，只要能转化为整形就可以用这个
template<class T>
struct HashFunc
{
	size_t operator()(const T& key)
	{
		return (size_t)key;
	}
};

//因为字符串做键值非常常见，库里面也特化了一份
//字符串哈希算法这里不展开讲，我这里采用的是BKDR算法
template<>
struct HashFunc<string>
{
	size_t operator()(const string& key)
	{
		size_t hashi = 0;
		for (auto ch : key)
		{
			hashi = hashi * 31 + ch;
		}
		return hashi;
	}
};

namespace hash_bucket
{
	template<class K, class V>
	struct HashNode
	{
		HashNode* _next;
		pair<K, V> _kv;

		HashNode(const pair<K, V>& kv)
			:_kv(kv)
			, _next(nullptr)
		{}
	};

	template<class K, class V, class Hash = HashFunc<K>>
	class HashTable
	{
		typedef HashNode<K, V> Node;
	public:
		HashTable()
		{
			_tables.resize(10);
		}

		//节点是自己new的，需要写析构函数，遍历即可
		~HashTable()
		{
			for (size_t i = 0; i < _tables.size(); i++)
			{
				Node* cur = _tables[i];
				while (cur)
				{
					Node* next = cur->_next;
					delete cur;
					cur = next;
				}
				_tables[i] = nullptr;
			}
		}

		// 插入
		bool Insert(const pair<K, V>& kv)
		{
			if (Find(kv.first))  //原来已经存在不能插入
				return false;

			Hash hf;  //用来转化非数值类型为整形

			//对于开散列扩容
			if (_n == _tables.size())
			{
				vector<Node*> newTables;
				newTables.resize(_tables.size() * 2, nullptr);
				// 遍历旧表
				for (size_t i = 0; i < _tables.size(); i++)
				{
					Node* cur = _tables[i];
					while (cur)
					{
						//先记录下一个节点，防止断掉
						Node* next = cur->_next;

						// 挪动到映射的新表（头插）
						size_t hashi = hf(cur->_kv.first) % newTables.size();
						cur->_next = newTables[hashi];
						newTables[hashi] = cur;

						cur = next;
					}

					_tables[i] = nullptr;
				}

				_tables.swap(newTables);
			}

			size_t hashi = hf(kv.first) % _tables.size();
			Node* newnode = new Node(kv);

			// 新节点头插即可
			newnode->_next = _tables[hashi];
			_tables[hashi] = newnode;
			++_n;

			return true;
		}

		// 查找
		Node* Find(const K& key)
		{
			Hash hf;
			// 找到对应的桶遍历即可
			size_t hashi = hf(key) % _tables.size();
			Node* cur = _tables[hashi];
			while (cur)
			{
				if (cur->_kv.first == key)
				{
					return cur;
				}

				cur = cur->_next;
			}

			return nullptr;
		}

		/// 删除
		bool Erase(const K& key)
		{
			Hash hf;
			// 先找到对应桶，遍历的同时记录前置节点，链表删除就不多讲了
			size_t hashi = hf(key) % _tables.size();
			Node* prev = nullptr;
			Node* cur = _tables[hashi];
			while (cur)
			{
				if (cur->_kv.first == key)
				{
					if (prev == nullptr)
					{
						_tables[hashi] = cur->_next;
					}
					else
					{
						prev->_next = cur->_next;
					}
					delete cur;

					return true;
				}

				prev = cur;
				cur = cur->_next;
			}

			return false;
		}

		//测试接口，大家可以随机生成大量数据插入看看每个桶的平均长度，应该1-2左右
		void Some()
		{
			size_t bucketSize = 0;
			size_t maxBucketLen = 0;
			size_t sum = 0;
			double averageBucketLen = 0;

			for (size_t i = 0; i < _tables.size(); i++)
			{
				Node* cur = _tables[i];
				if (cur)
				{
					++bucketSize;
				}

				size_t bucketLen = 0;
				while (cur)
				{
					++bucketLen;
					cur = cur->_next;
				}

				sum += bucketLen;

				if (bucketLen > maxBucketLen)
				{
					maxBucketLen = bucketLen;
				}
			}

			averageBucketLen = (double)sum / (double)bucketSize;

			printf("all bucketSize:%d\n", _tables.size());
			printf("bucketSize:%d\n", bucketSize);
			printf("maxBucketLen:%d\n", maxBucketLen);
			printf("averageBucketLen:%lf\n\n", averageBucketLen);
		}

	private:
		vector<Node*> _tables;
		size_t _n = 0;
	};
}

4.3开闭散列的对比

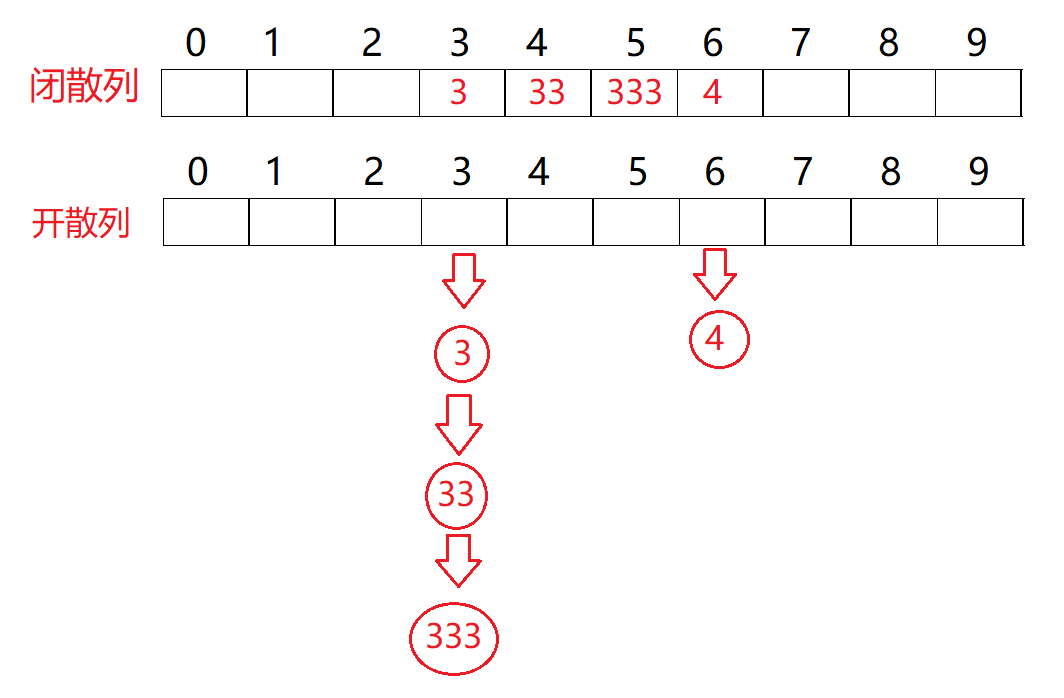
先说结论：实际中开散列使用较多，C++STL中unordered_map和unordered_set底层是开散列。
原因：开散列采用拉链解决处理冲突的方式不会干扰其它位置，可以有效的提高哈希表插入和查找效率。
以线性探测解决冲突为例，向闭散列(空间为10)中插入3、33、333、4，4会因为冲突移动到下标6位置，查找4的时候就会多查找几次。开散列就没有这样的问题。
在这里插入图片描述