CT3D
- 一、RPN for 3D Proposal Generation
- 二、Proposal-to-point Encoding Module
- 2.1、Proposal-to-point Embedding
- 2.2、Self-attention Encoding
- 三、Channel-wise Decoding Module
- 3.1、Standard Decoding
- 3.2、Channel-wise Re-weighting
- 3.3、Channel-wise Decoding Module
- 四、Detect head and Training Targets
- 五、训练losses
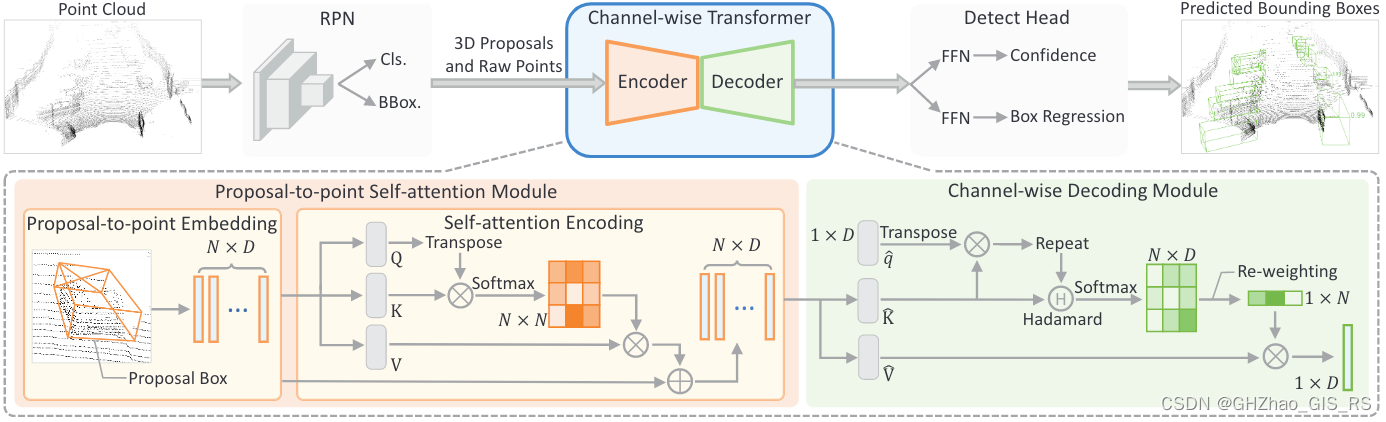
一、RPN for 3D Proposal Generation
就是基于单阶段的网络获取box作为Proposal,文章中使用的是Second网络,其他的如pointpillar、centerpoint都可以作为
CT3D的RPN网络。
二、Proposal-to-point Encoding Module
通过以下两个模块精修RPN输出的proposal:
1、将proposal特征映射到点的特征上(下图左)。
2、通过自注意力编码对proposal内点之间的相对关系进行建模来细化点的特征(下图右)。
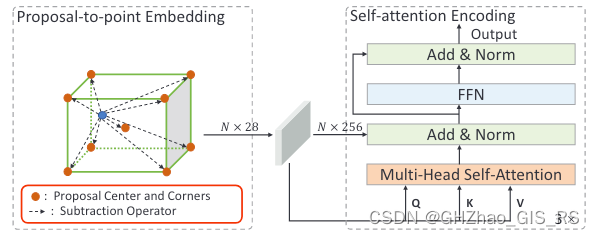
2.1、Proposal-to-point Embedding
对于给定的一个proposal,选择ROI区域内的点,ROI区域是一个没有高度限制的圆柱体,然后随机选取ROI范围内的256个点。
- 首先计算采样点和Proposal中心点的相对坐标, Δ p i c = p i − p c , ∀ p i ∈ N \Delta \boldsymbol{p}_{i}^{c}=\boldsymbol{p}_{i}-\boldsymbol{p}^{c}, \forall \boldsymbol{p}_{i} \in \mathcal{N} Δpic=pi−pc,∀pi∈N。
- 然后一个直接的做法是将Proposal的长、宽、高、和旋转角度信息直接拼接到每个点的特征上,即 [ Δ p i c , l c , w c , h c , θ c , f i r ] \left[\Delta \boldsymbol{p}_{i}^{c}, l^{c}, w^{c}, h^{c}, \theta^{c}, f_{i}^{r}\right] [Δpic,lc,wc,hc,θc,fir]。由于Transformer 编码器根据这种几何信息重新定向的效果可能较差,所以这种直接基于尺寸和方向的特征表示对于Proposal的优化帮助可能是有限的。
- 通过计算采样点和Proposal八个顶点的相对位置, Δ p i j = p i − p j , j = 1 , … , 8 \Delta \boldsymbol{p}_{i}^{j}=\boldsymbol{p}_{i}-\boldsymbol{p}^{j}, j=1, \ldots, 8 Δpij=pi−pj,j=1,…,8, p j {p}^{j} pj是第 j j j个顶点的坐标,这样长、宽、高和角度信息就被重新编码为不同纬度的距离信息。
- 最后将上述信息合并,并经多一个MLP网络上提升特征纬度。
f i = A ( [ Δ p i c , Δ p i 1 , … , Δ p i 8 , f i r ] ) ∈ R D \boldsymbol{f}_{i}=\mathcal{A}\left(\left[\Delta \boldsymbol{p}_{i}^{c}, \Delta \boldsymbol{p}_{i}^{1}, \ldots, \Delta \boldsymbol{p}_{i}^{8}, f_{i}^{r}\right]\right) \in \mathbb{R}^{D} fi=A([Δpic,Δpi1,…,Δpi8,fir])∈RD
2.2、Self-attention Encoding
随后将重新编码后的采样点送入多头自注意力层,然后接一个带有残差结构的FFN网络。除了没有位置编码外(在第一步中已经包含了位置信息),这种自注意力编码机制和NLP中的Transofrmer结构几乎一模一样。encoding具体细节略过。
三、Channel-wise Decoding Module
3.1、Standard Decoding
3.2、Channel-wise Re-weighting
3.3、Channel-wise Decoding Module
四、Detect head and Training Targets
将经过编码-解码模块的输出送入两个FFN网络中,预测得到confidence和相对于输入的Proposal的box残差值。
训练过程中confidence的真值被设置为Proposals和对应的gt的3D IoU值。confidence真值计算公式如下:
c
t
=
min
(
1
,
max
(
0
,
I
o
U
−
α
B
α
F
−
α
B
)
)
c^{t}=\min \left(1, \max \left(0, \frac{\mathrm{IoU}-\alpha_{B}}{\alpha_{F}-\alpha_{B}}\right)\right)
ct=min(1,max(0,αF−αBIoU−αB))
box回归值的真值计算如下:
x
t
=
x
g
−
x
c
d
,
y
t
=
y
g
−
y
c
d
,
z
t
=
z
g
−
z
c
h
c
,
l
t
=
log
(
l
g
l
c
)
,
w
t
=
log
(
w
g
w
c
)
,
h
t
=
log
(
h
g
h
c
)
,
θ
t
=
θ
g
−
θ
c
,
\begin{aligned} x^{t} & =\frac{x^{g}-x^{c}}{d}, y^{t}=\frac{y^{g}-y^{c}}{d}, z^{t}=\frac{z^{g}-z^{c}}{h^{c}}, \\ l^{t} & =\log \left(\frac{l^{g}}{l^{c}}\right), w^{t}=\log \left(\frac{w^{g}}{w^{c}}\right), h^{t}=\log \left(\frac{h^{g}}{h^{c}}\right), \\ \theta^{t} & =\theta^{g}-\theta^{c}, \end{aligned}
xtltθt=dxg−xc,yt=dyg−yc,zt=hczg−zc,=log(lclg),wt=log(wcwg),ht=log(hchg),=θg−θc,
五、训练losses
CT3D是端到端的训练策略,包括三个损失,分别是RPN损失、confidence损失、box回归损失。

confidence损失用的是二元交叉墒计算。
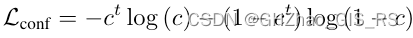
回归损失使用的是Smooth-L1计算,只有
I
o
U
≥
α
R
IoU ≥ α_R
IoU≥αR 的Proposal才会用来计算回归损失。
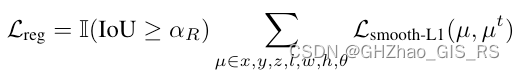



![[个人笔记] Zabbix实现Webhook推送markdown文本](https://img-blog.csdnimg.cn/4926724b345946728d80d12c1d210584.png)