第十章 单调栈part02

503. 下一个更大元素 II

给定一个循环数组 nums （ nums[nums.length - 1] 的下一个元素是 nums[0] ），返回 nums 中每个元素的 下一个更大元素 。

数字 x 的 下一个更大的元素 是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。

思路：比较简单粗暴，手动把数组延长两杯然后按单调栈求下一个最大元素，最后在把结果数组取前一半。

class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) {
        vector<int> new_nums(2*nums.size()-1,0);
        for(int i=0;i<nums.size();i++){
            new_nums[i]=nums[i];
        }
        for(int i=nums.size();i<2*nums.size()-1;i++){
            new_nums[i]=nums[i-nums.size()];
        }
        stack<int> st;
        st.push(0);
        vector<int> result(new_nums.size(),-1);
        for(int i=0;i<new_nums.size();i++){
            while(!st.empty()&&new_nums[i]>new_nums[st.top()]){
                result[st.top()]=new_nums[i];
                st.pop();
            }
            st.push(i);
        }
        vector<int> res(nums.size(),0);
        for(int i=0;i<nums.size();i++){
            res[i]=result[i];
        }
        return res;
    }
};

 可以直接在原数组操作，减少空间使用：

class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) {
        vector<int> result(nums.size(),-1);
        stack<int> st;
        for(int i=0;i<2*nums.size();i++){
            while(!st.empty()&&nums[i%nums.size()]>nums[st.top()]){
                result[st.top()]=nums[i%nums.size()];
                st.pop();
            }
            st.push(i%nums.size());
        }
        return result;
    }
};

42. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

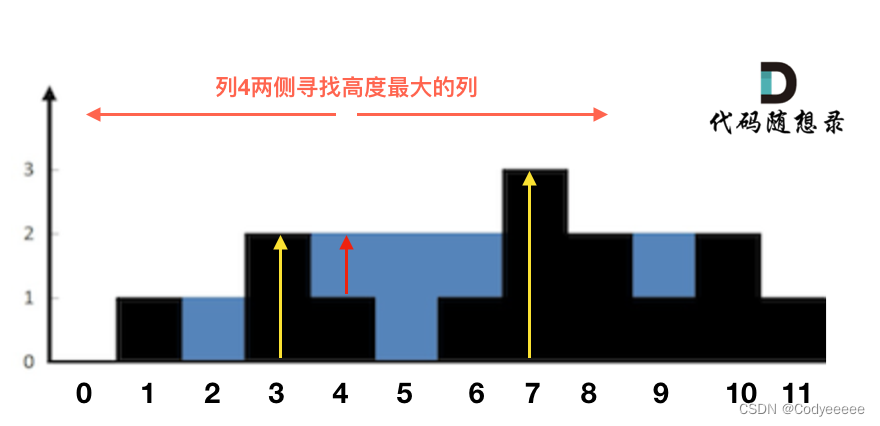
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

暴力法都没写出来，主要思路是按列计算，对每一列找左边和右边的最高柱子，其中取矮的一个，减去当前高度即可求出当前列蓄水的最大高度。但是暴力法也是超时的

class Solution {
public:
    int trap(vector<int>& height) {
        int sum=0;
        for(int i=0;i<height.size();i++){
            if(i==0||i==height.size()-1)  continue;
            int lheight=height[i];
            int rheight=height[i];
            for(int m=0;m<i;m++){
                if(height[m]>lheight)  lheight=height[m];
            }
            for(int n=height.size()-1;n>i;n--){
                if(height[n]>rheight)  rheight=height[n];
            }
            sum+=min(lheight,rheight)-height[i];
        }
        return sum;
    }
};

 双指针法：

暴力算法中对左右的最高柱子的计算其实是有重复的，可以通过双指针辅助从而减少重复计算。时间复杂度从O（n^2）降为O(n）。

class Solution {
public:
    int trap(vector<int>& height) {
        vector<int> maxLeft(height.size(),0);
        vector<int> maxRight(height.size(),0);
        maxLeft[0]=height[0];
        for(int i=1;i<height.size();i++){
            maxLeft[i]=max(maxLeft[i-1],height[i]);
        }
        maxRight[height.size()-1]=height[height.size()-1];
        for(int i=height.size()-2;i>=0;i--){
            maxRight[i]=max(maxRight[i+1],height[i]);
        }
        int sum=0;
        for(int i=1;i<height.size()-1;i++){
            sum+=min(maxLeft[i],maxRight[i])-height[i];
        }
        return sum;
    }
};

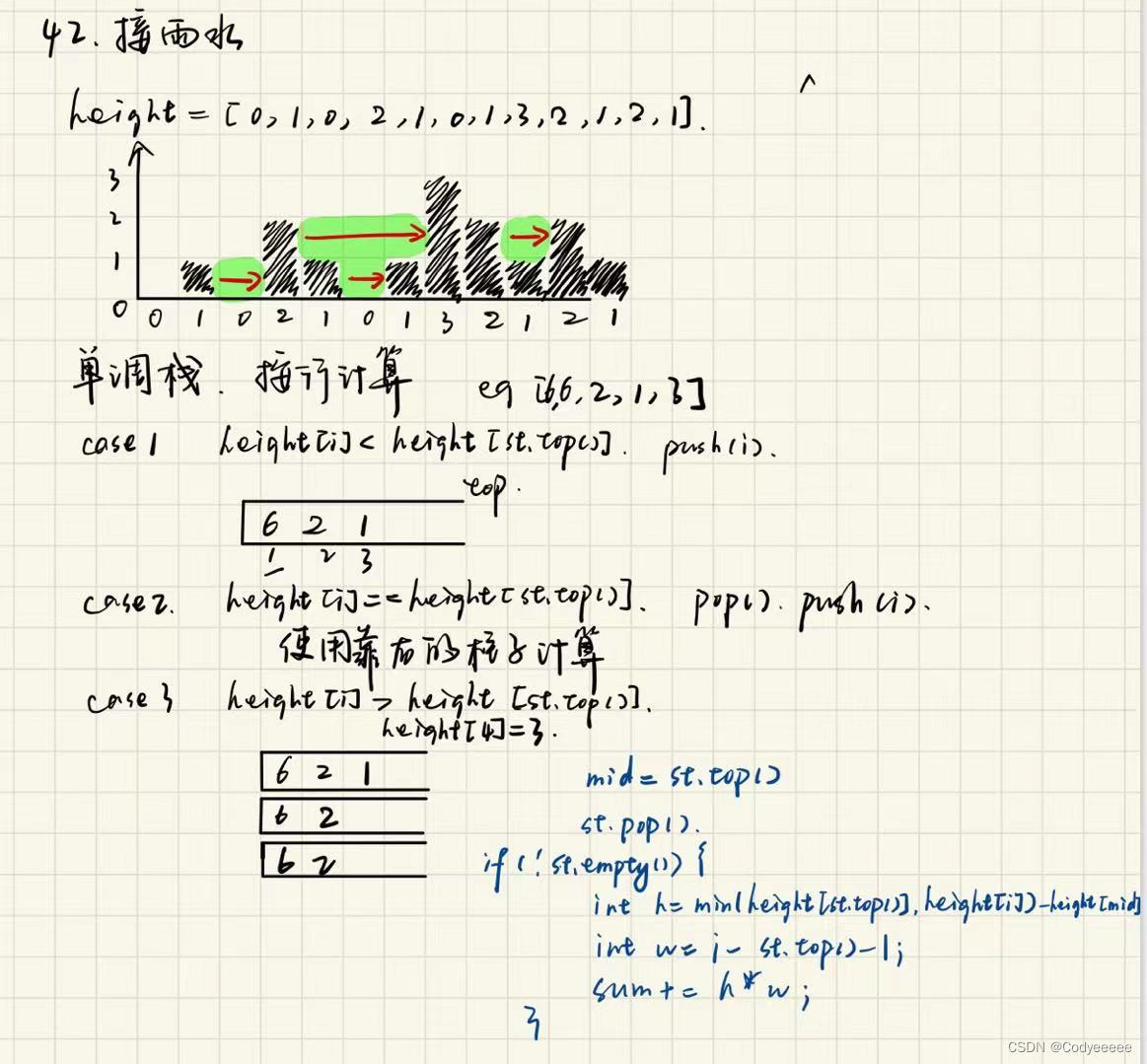
单调栈法：

前面的解法都是按列计算，使用单调栈是按行计算。

class Solution {
public:
    int trap(vector<int>& height) {
        int sum=0;
        stack<int> st;
        st.push(0);
        for(int i=1;i<height.size();i++){
            if(height[i]<height[st.top()])  st.push(i);
            if(height[i]==height[st.top()]){
                st.pop();
                st.push(i);
            }
            else{
                while(!st.empty()&&height[i]>height[st.top()]){
                    int mid=st.top();
                    st.pop();
                    if(!st.empty()){
                        int h=min(height[i],height[st.top()])-height[mid];
                        int w=i-st.top()-1;
                        sum+=h*w;
                    }
                }
                st.push(i);
            }
        }
        return sum;
    }
};