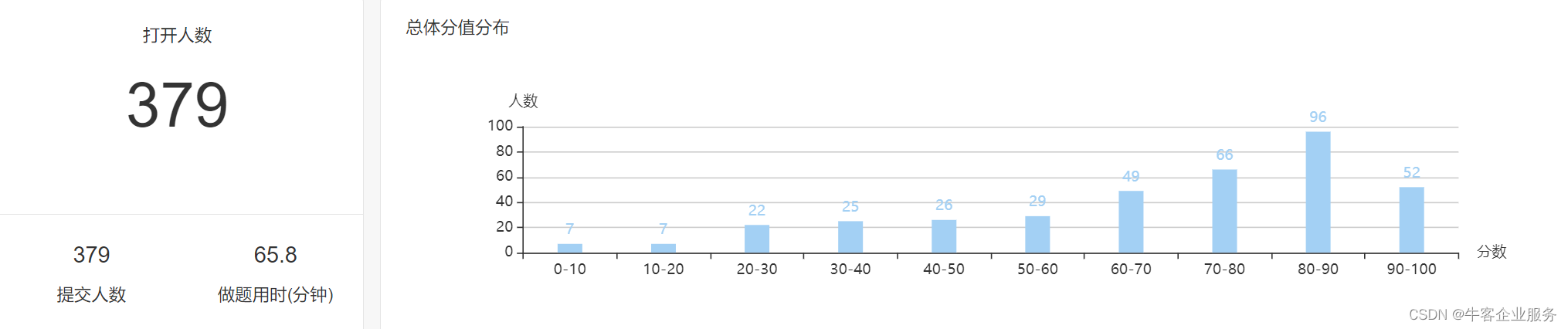
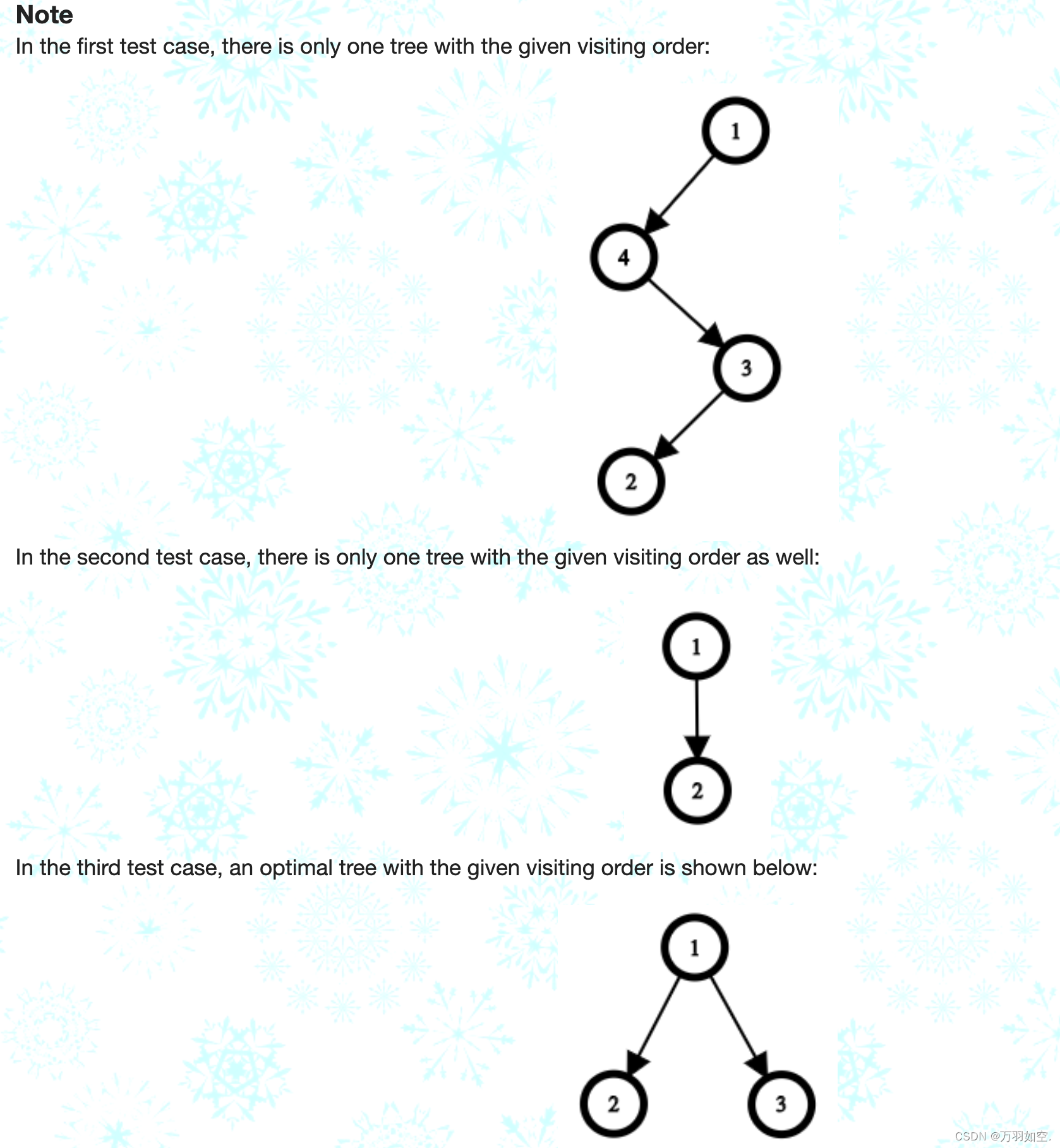
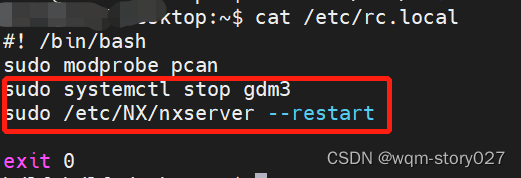
前言
位运算是在算法设计中的一种非常重要和高效的方法,常见的有与运算,非运算,异或运算。我们常用的比较多的可能就是异或运算,又叫无进位相加。
1.1 取非运算----(~)
取非运算其实就是和我们的无符号数取反码类似,就是将数对应的二进制所有位取反,0变为1,1变为0;
如15的二进制形式为1111 ,则15的非~15就是为0000
如17的二进制形式10001 , 则17的非~17就是01110
1.2与运算-----(&)
与运算就是只有当两个数同时为1时最后结果才会为1,否则只要有一放为0,则最终结果就为0;
如15的二进制形式为1111 ,如17的二进制形式10001
则15&17=1111&10001=00001,最终结果为1
1.3异或运算-----(^)
这里异或符号就是我们机组中的圈里面一个+,异或叫无进位相加。指的是0异或任何数都为任何数,任何数异或本身都为0。异或运算满足结合律。
0^0=0, 1^1=0, 0^1=1
2. 位运算相关运用
2.1. 交换两个数据
我们可以利用异或运算的特性来交换两个数的位置,而不需要开辟多余空间,更重要的是位运算的速率是非常快的。
a=a^b //改行执行后 a=a^b b=b
b=a^b //改行执行后 a=a^b b=a^b^b=a
a=a^b //改行执行后 a=a^b^a=b b=a
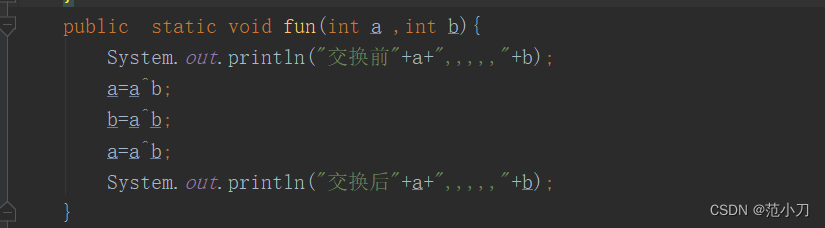
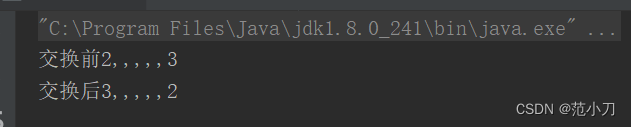
public static void fun(int a ,int b){
System.out.println("交换前"+a+",,,,,"+b);
a=a^b;
b=a^b;
a=a^b;
System.out.println("交换后"+a+",,,,,"+b);
}
则最后成功交换过来了。
注
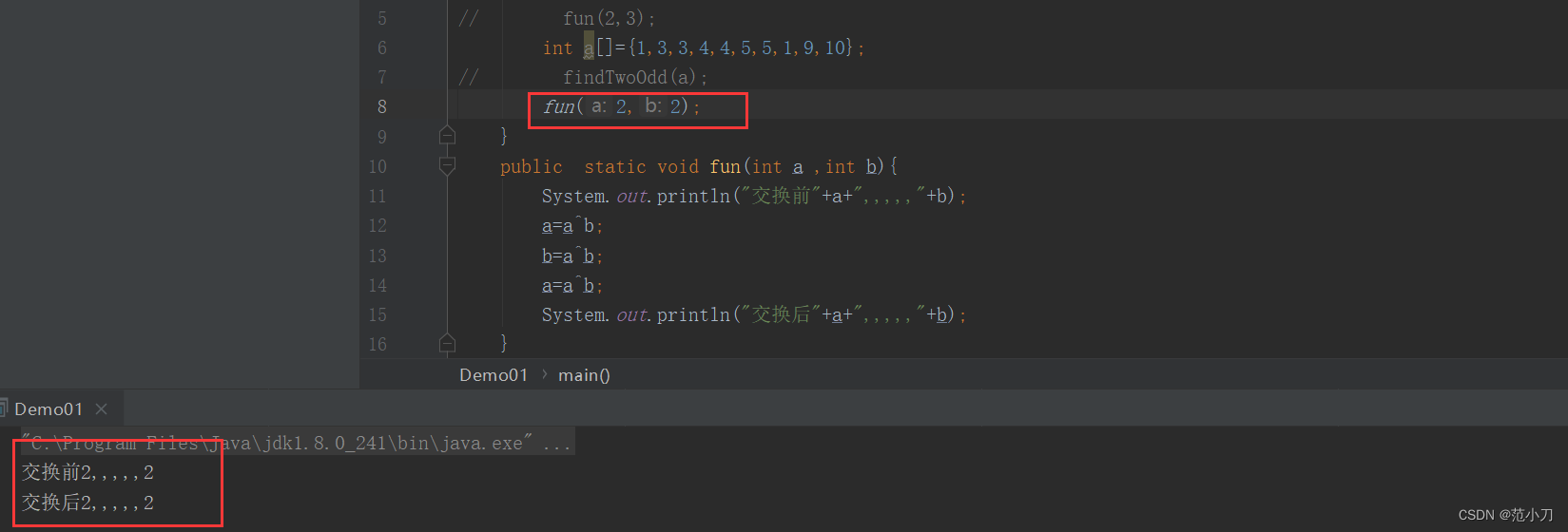
用为交换两个数时,两个数的值是可以相同的,但是两个数不能指向同一个内存,你要指向同一个内存就相当于对同一个数进行异或运算,最后结果就会被消为0.
2.2 一个数组中有一种数出现了奇数次,其他数都出现了偶数次,怎么找到这一个数
当一组数只有一个数出现了,奇数次则寻找起来还是比较简单的,直接将所有数异或就可以了。
比如为a,b,b,b,b,c,c,d,d.
相同数异或为0.则偶数个相同的数异或在一起就是为0.则最后就只会保留那个出现奇数次的数。
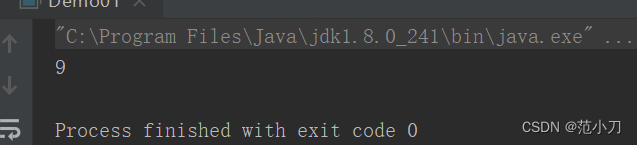
public static int findodd(int a[]){
int count=0;
for (int x:a){
count^=x;
}
return count;
}


2.3 一个数组中有两种数出现了奇数次,其他数都出现了偶数次,怎么找到这两个数
当出现了两个奇数次数,方法相同只是多加了一步。首先还是先将所有的数都异或到一起。结果为哪两个奇数次的异或。
如a,b,c,c,d,d,e,e,f,f.
这全部异或到一起的结果为a^b用eor表示。
因为a和b为两个不同的数,这eor一定不会为0.既然不为0,这eor所表示的二进制必定存在一位为1,假设第三位为1.eor=xxxxxx100.这是eor所表示的二进制位,第三位不为0.然后我们就可以帮所有的数分为两类,一类为第三位为1,一类为第三位为0.因为第三位不是1就一定是0.
**且两个奇数次数一定分布在两个不同的区域里。
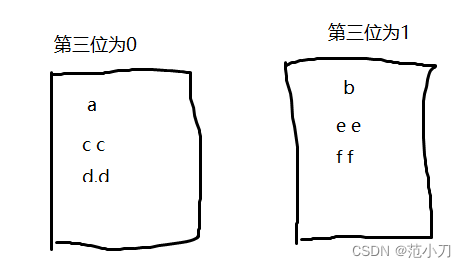
然后将第三位为0的这一区域所有数异或起来。用eor1表示为a或b
则最终eor=a^b, eor1=a或b.
则若eor1=a 则eor^eor1=b
则若eor1=b 则eor^eor1=a.
则最终两个数为eor1和eor1^eor.
2.3.1 如何找到第一位不为0,也就是说你怎么找到a^b的第三位。
这里就需要用到一个公式,找到右侧第一位不为0的数。
int right=eor&(~eor+1); //取出最右侧不为0的数
如eor=1000100,
~eor=0111011+1=0111100&1000100=0000100
代码为
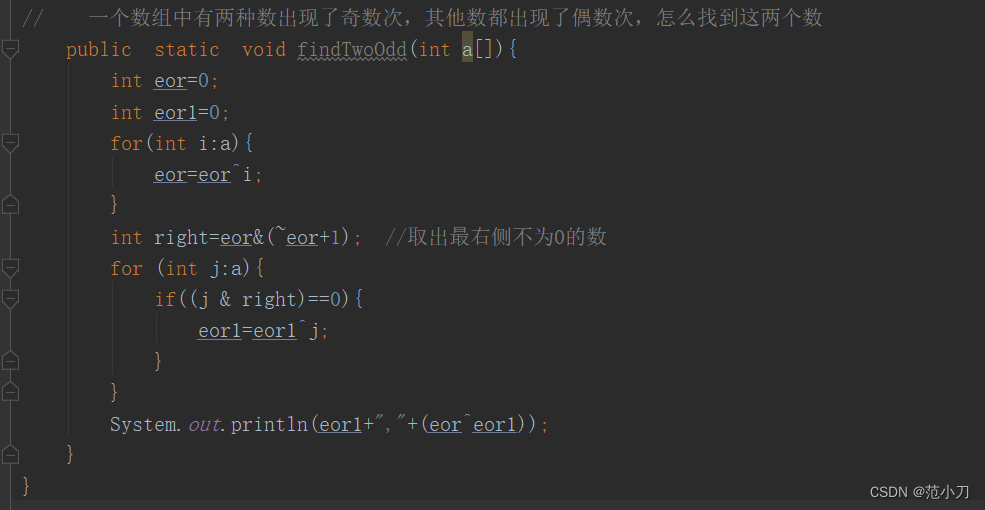
// 一个数组中有两种数出现了奇数次,其他数都出现了偶数次,怎么找到这两个数
public static void findTwoOdd(int a[]){
int eor=0;
int eor1=0;
for(int i:a){
eor=eor^i;
}
int right=eor&(~eor+1); //取出最右侧不为0的数
for (int j:a){
if((j & right)==0){
eor1=eor1^j;
}
}
System.out.println(eor1+","+(eor^eor1));
}


3,思考
若题目中不告诉你有多少个数出现了奇数次,让你找出所有出现奇数次的数,能否用位运算找出?若可以找出则应该怎么找出?