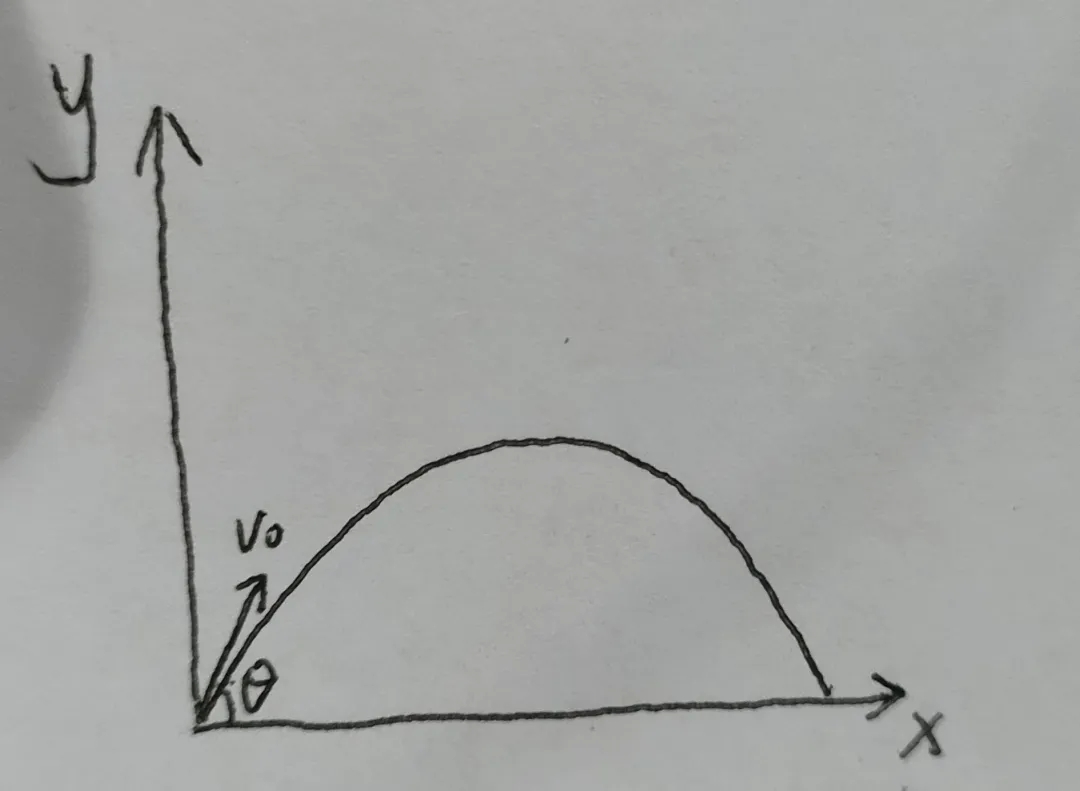
已知:斜抛物体的初速度为 v 0 v_0 v0(与水平方向的夹角为 θ \theta θ),重力加速度为 g g g。
求:抛物轨迹方程?
垂直方向的速度为
v
y
=
v
0
sin
θ
−
g
t
v_y=v_0 \sin \theta -gt
vy=v0sinθ−gt
水平方向的速度为
v
x
=
v
0
cos
θ
v_x=v_0 \cos \theta
vx=v0cosθ
垂直方向的位移为
y = ∫ v y d t = ∫ ( v 0 sin θ − g t ) d t = v 0 t sin θ − g t 2 2 y=\int v_ydt=\int (v_0 \sin \theta -gt)dt=v_0t \sin \theta-\frac{gt^2}{2} y=∫vydt=∫(v0sinθ−gt)dt=v0tsinθ−2gt2
水平方向的位移为
x = ∫ v x d t = ∫ ( v 0 cos θ ) d t = v 0 t cos θ x=\int v_xdt=\int (v_0 \cos \theta)dt=v_0t \cos \theta x=∫vxdt=∫(v0cosθ)dt=v0tcosθ
将x代入y即可得到轨迹方程
y = t a n θ x − g 2 v 0 2 cos 2 θ x 2 y=tanθx-\frac{g}{2v_0^2\cos^2θ}x^2 y=tanθx−2v02cos2θgx2
令y=0,可得
x = 2 sin θ cos θ v 0 2 g = v 0 2 sin 2 θ g x = \frac{2\sin\theta \cos\theta v_0^2}{g}=\frac{v_0^2 \sin2 \theta }{g} x=g2sinθcosθv02=gv02sin2θ
当 θ = 45 ° \theta=45° θ=45°时, x m a x = v 0 2 g x_{max}=\frac{v_0^2}{g} xmax=gv02



![用友NC Cloud uploadChunk任意文件上传漏洞复现 [附POC]](https://img-blog.csdnimg.cn/f412625fbf3e44e7a3a09bd798bb5f85.png)