算法设计与分析复习--回溯（一）

news2024/11/18 6:03:24

文章目录

上一篇
回溯法性质
子集和问题
装载问题
0-1背包问题
下一篇

算法设计与分析复习–贪心（二）

回溯法性质

类似穷举的搜索尝试过程，在搜索尝试过程中寻找问题的解，组织得井井有条（避免遗漏），高效（剪裁避免不必要搜索）

使用深度优先的搜索策略（DFS + 剪枝）

回溯法的阶梯框架：

子集树算法框架
排序树算法框架

在这里插入图片描述

结点类型：

活结点：自身已生成但是其儿子还没有全部生成
拓展结点：正在产生儿子的结点
死结点：不满足约束或所有儿子已经产生，不能向纵深方向移动

为了避免生成那些不可能产生最优解的问题状态，要不断利用限界函数，处死结点=>剪枝

剪枝策略：

可行性剪枝，左剪枝
最优性剪枝，右剪枝
交换搜索顺序，排序方式变化

解空间类型：

子集树：所给的问题是从n个元素集合S中找出满足某种性质的子集。
排列数：所给问题是确定n个元素满足某种性质的排列。

采用交换方式实现的全排列（顺序有点问题）

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 10;

int a[N], n;
int path[N];

void dfs(int* ans, int k)
{
    if (k == n - 1){
        for (int i = 0; i < n; i ++)
            printf("%d ", ans[i]);
        puts("");
    }
    
    for (int i = k; i < n; i ++){
        swap(ans[k], ans[i]);
        dfs(ans, k + 1);
        swap(ans[k], ans[i]);
    }
}

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++) path[i] = i + 1;
    
    dfs(path, 0);
    return 0;
}

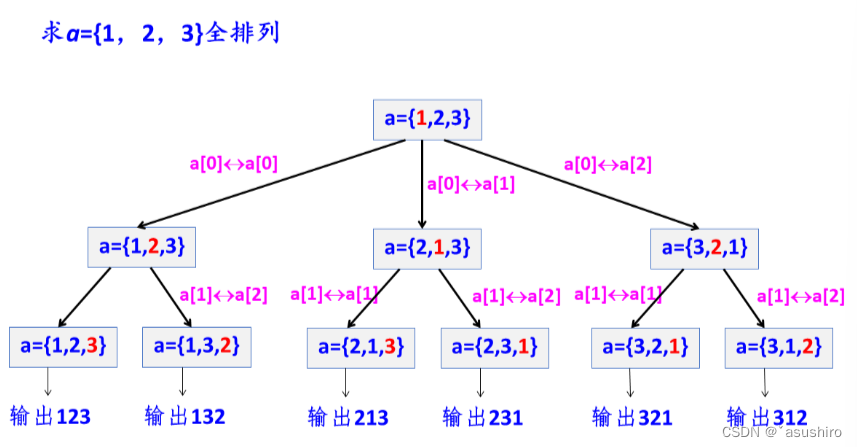
在这里插入图片描述

基于子集树框架的问题求解：

子集和问题
装载问题
0-1背包问题
图的m着色问题

基于排列树框架的问题求解：

旅行商问题(TSP）
N皇后问题

子集和问题

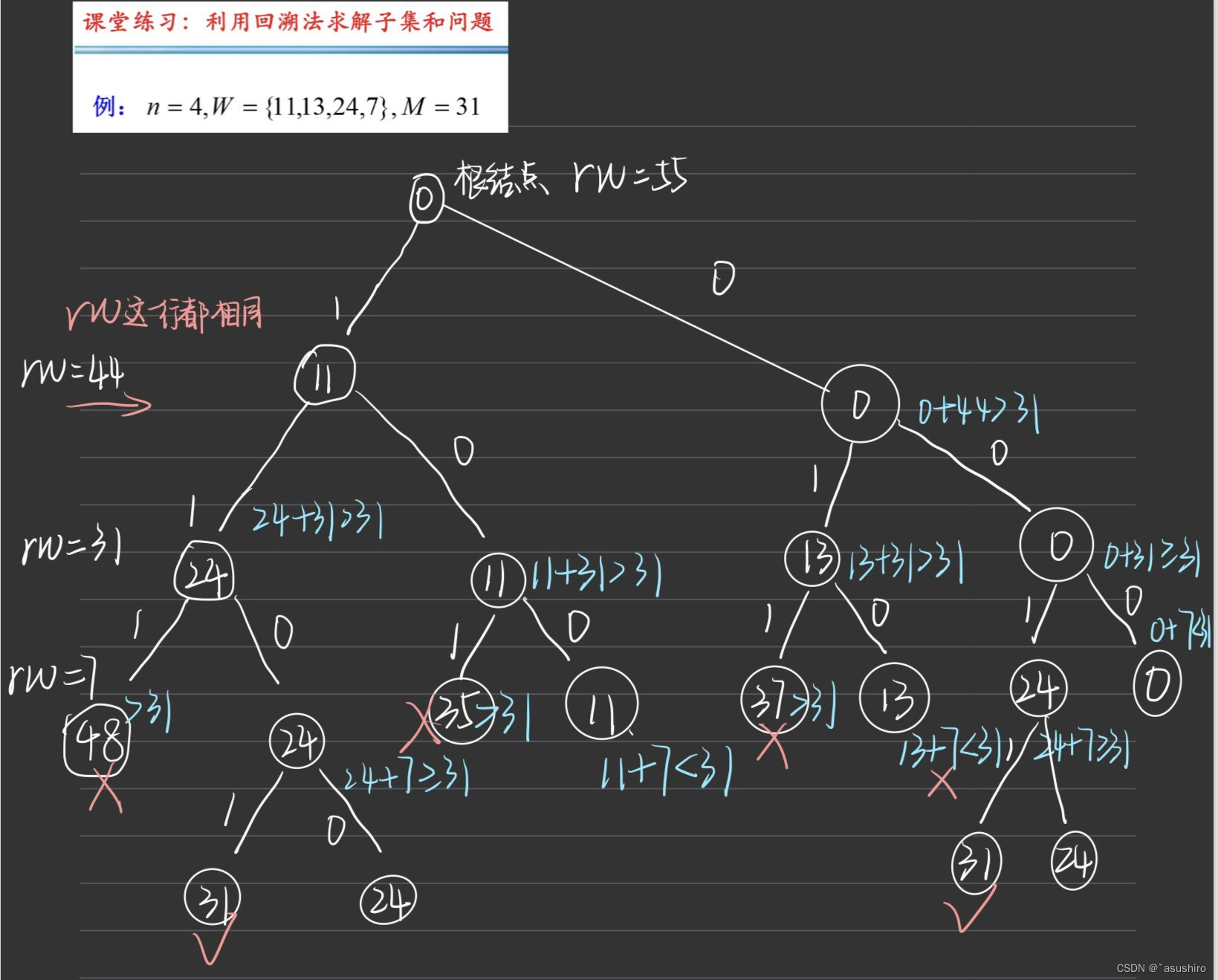
问题描述：给定n个不同正实数的集合W = {w(i) | 1 <= i <= n}和一个正整数M，要求找到子集S使得求和为M。

子集和问题要求出所有可行解

左剪枝：求和不超过M => cw + a[i] <= M
右剪枝：当前已选的价值与剩余的数的价值的和要大于M否则不可能找到 => cw + rw >= M

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 110;

int a[N], n, M, cw, rw;
vector<int> ans;

void dfs(int k)
{
    if (k == n)//根节点是0叶结点就是n
    {
        if (cw == M){
            for(auto i : ans)
                printf("%d ", i);
            puts("");
        }
        return;
    }
    rw -= a[k];
    if (cw + a[k] <= M){//左剪枝条件
        cw += a[k];
        ans.push_back(a[k]);
        dfs(k + 1);//向左走
        ans.pop_back();
        cw -= a[k];
    }
    if(rw + cw >= M)//右剪枝条件
        dfs(k + 1);//向右走
        
    rw += a[k];
}

int main()
{
    scanf("%d%d", &n, &M);
    
    for (int i = 0; i < n; i ++) scanf("%d", &a[i]), rw += a[i];
    
    dfs(0);
    return 0;
}

在这里插入图片描述

装载问题

和贪心中的装载问题不同
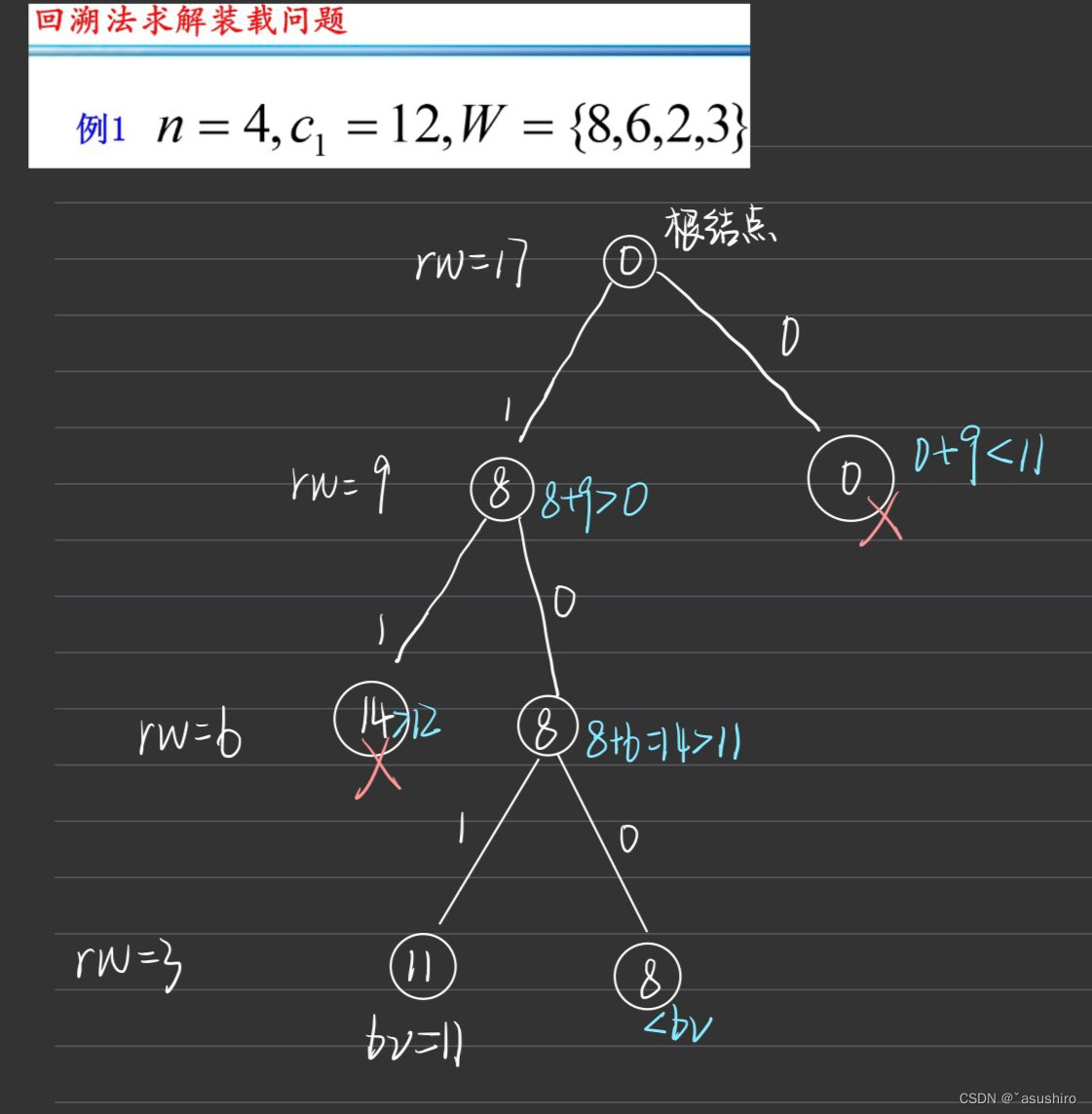
问题描述：n个集装箱要装到2艘载重量分别c1,c2的货轮，其中集装箱 $i$ 的重量为 $w_i$ 。要求找到合理的装载方案将这n个货箱装上这2艘轮船。

要使两个船都装上，可以考虑将第一个船尽可能装满，然后将剩下的货物装在第二艘船上，如果没超重就是可行的，将考虑两个船的问题转换成考虑一个。

为找到将左边轮船撞得最满的方案，用bestw进行限界

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 110;

int a[N], n, c1, c2;
int cw, bw, rw, other;
vector<int> ans;

void dfs(int k)
{
    if (k == n){
        bw = cw;
        if(other > c2) return;//other是另一艘船货物重量
        for (auto i : ans)
            printf("%d ", i);
        puts("");
        return;
    }
    
    rw -= a[k];
    if (cw + a[k] <= c1)
    {
        cw += a[k];
        ans.push_back(a[k]);
        dfs(k + 1);
        ans.pop_back();
        cw -= a[k];
    }
    if (cw + rw >= bw){
        other += a[k];
        dfs(k + 1);
        other -= a[k];
    }
    rw += a[k];
    
}

int main()
{
    scanf("%d%d%d", &n, &c1, &c2);
    
    for (int i = 0; i < n; i ++) scanf("%d", &a[i]), rw += a[i];
    
    dfs(0);
    return 0;
}

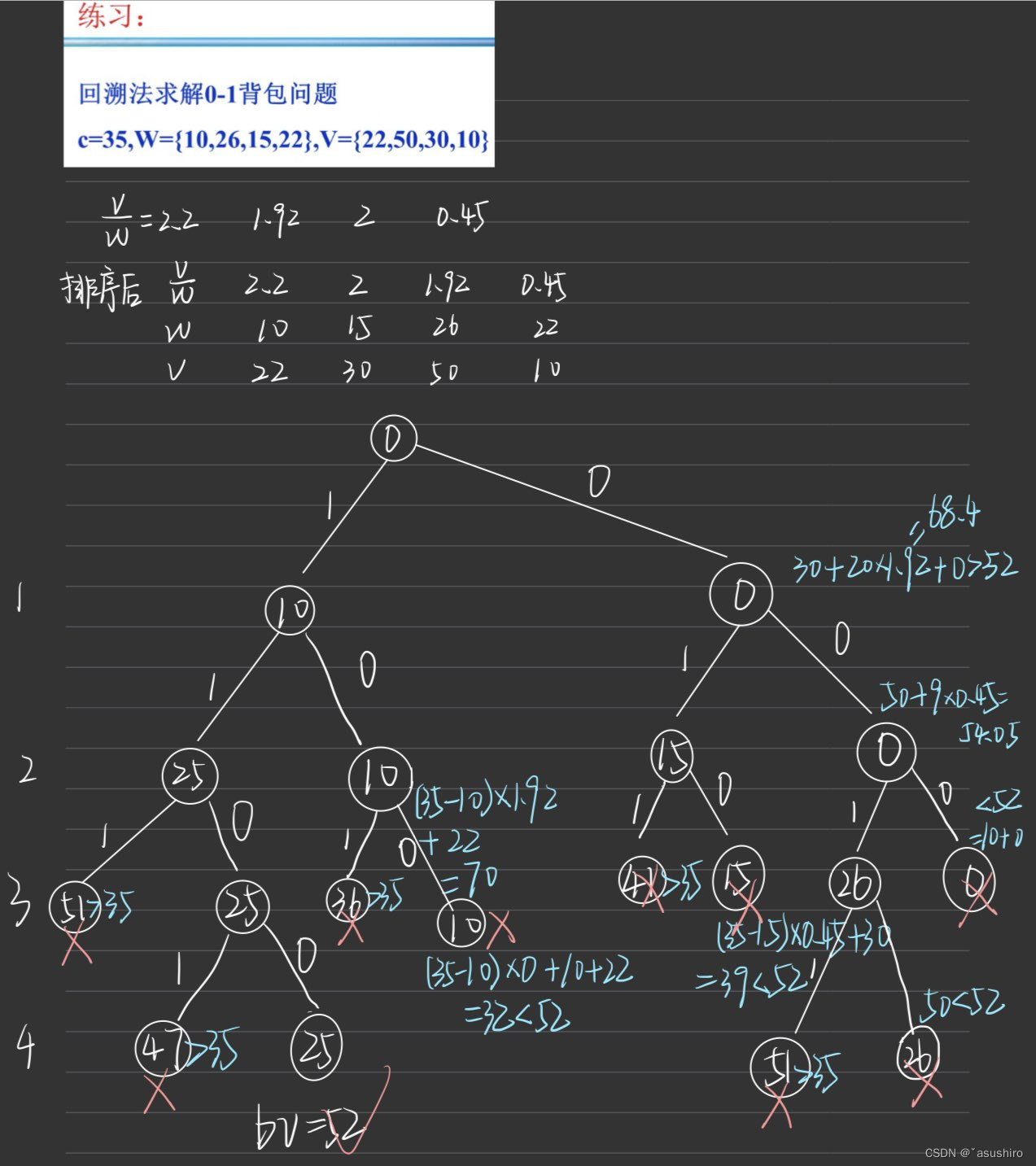
在这里插入图片描述

0-1背包问题

问题描述：给定n中物品和一个背包。物品 $i$ 的重量是 $w_i$ ，其价格为 $v_i$ , 背包容量为 $c$ 。问如何选择装入背包中的物品，使得装入背包物品的总价值最大？

左剪枝：满足背包容量即可

右剪枝：右剪枝就是求剩余背包重量rw = c - cw中贪心背包的最优价值，由于允许部分装入，所以一定比0-1背包装的满价值更大，结果是剩余价值的一个上界，允许右剪枝的条件更加宽松。
$\sum{v_j}(不超过背包剩余重量的物品价值) + (背包剩余重量) * （不被放入的物品的单位价值）【部分装入的结果】$
限界函数：
$c v + r v >= b v$

交换搜索顺序：由于用到了贪心背包，所以按照物品单价从大到小的方式进行搜索。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
typedef pair<double, double> PII;

const int N = 110;

double w[N], v[N];
int n, c;
double cw, cv, bv;
vector<PII> ob, x;//x用来记录当前的搜索顺序
vector<PII> ans;//最优解，解只有一个，将这个迭代的解记录

bool cmp(PII x, PII y)
{
    return (x.second / x.first) > (y.second / y.first);
}

bool bound(int rw, int k)
{
    int i = k + 1;
    double rv = cv;
    //printf("cv: %.2lf rw: %d\n", cv, rw);
    while(i <= n && ob[i].first <= rw)
    {
        rw -= ob[i].first;
        rv += ob[i].second;
        i ++;
    }
    //printf("比值：%.2lf rw:%d\n", ob[i].second / ob[i].first, rw);
    if (i <= n) rv += (ob[i].second / ob[i].first) * rw;
    //printf("%d = %.2lf\n", k, rv);
    return rv >= bv;
}

void dfs(int k)
{
    if (k == n){
        if (cv > bv){
            bv = cv;//更新最优结果
            ans = x;
        }
        return;
    }
    
    if (cw + ob[k].first <= c)
    {
        cw += ob[k].first;
        x.push_back(ob[k]);
        cv += ob[k].second;
        dfs(k + 1);
        cv -= ob[k].second;
        x.pop_back();
        cw -= ob[k].first;
    }
    if(bound(c - cw, k))
    {
        dfs(k + 1);
    }
}

int main()
{
    scanf("%d%d", &n, &c);
    
    for (int i = 0; i < n; i ++) scanf("%lf", &w[i]);
    for (int i = 0; i < n; i ++) scanf("%lf", &v[i]);
    for (int i = 0; i < n; i ++) ob.push_back({w[i], v[i]});
    
    sort(ob.begin(), ob.end(), cmp);
    
    dfs(0);
    
    puts("对应物品的重量和价值:");
    for (auto i : ans)
        printf("{%d, %d} ", (int)i.first, (int)i.second);
    puts("\n最优价值：");
    printf("%d", (int)bv);
    return 0;
}

在这里插入图片描述