题目描述
思路
怎么得到这个序列中每一段的关系?
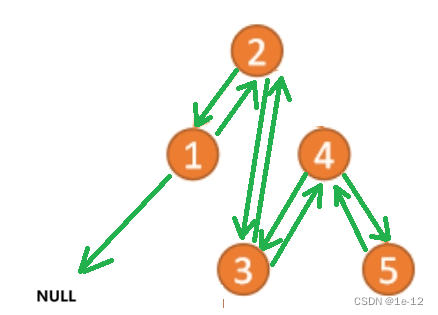
我们可以把这个只包含0和1的序列看作一个数组,0表示当前位置为0,1表示当前位置为1,利用前缀和的性质可以知道某一段中所包含的1的数量 sum1 = a[r] - a[l-1] 如果sum1为偶数,那么a[r] 和 a[l-1]的奇偶性相同 如果sum1为奇数,那么a[r] 和 a[l-1]的奇偶性不同 找到它们之间的关系,我们就可以使用并查集来存储他们 为什么要离散化?
序列的长度小于等于1e9,然而序列中下标出现的次数最多为1e4,所以使用离散化 种类并查集
序列中某一段有两种关系,奇数个1、偶数个1 我们定义两个扩展域,1~n表示偶数,n + 1 ~ 2 * n表示奇数 每次知道一个关系之后,将偶数区域和奇数区域都进行处理,像枚举一样,不漏掉每一种情况 并查集中存储的是区域与区域之间的关系,如果有一个关系成立,那么这个集合中其它的关系都成立 代码实现
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 1e4 + 10;
int fa[2 * N]; // 两个扩展域:1~N表示偶数关系,N+1~2N表示奇数关系
int n, m;
vector<int> ans; // 离散化数组
struct node // 结构体,存储每一段区间的左右端点
{
int x, y;
string op;
}a[N];
int get(int u) // 二分查找,将原数据离散化成下标
{
int l = 0, r = ans.size();
while(l + 1 != r)
{
int mid = l + r >> 1;
if(ans[mid] < u) l = mid;
else r = mid;
}
return r;
}
int find(int u) // 返回当前元素的祖宗元素,在哪个集合中
{
if(fa[u] != u) fa[u] = find(fa[u]);
return fa[u];
}
void merge(int x, int y) // 将x合并到y所在的集合中
{
fa[find(x)] = find(y);
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= m; i++)
{
cin >> a[i].x >> a[i].y >> a[i].op;
a[i].x--; // 因为利用了前缀和的性质,所以要将左端点-1,满足sum = a[r] - a[l-1]
ans.push_back(a[i].x);
ans.push_back(a[i].y);
}
sort(ans.begin(), ans.end()); // 将数据进行排序
ans.erase(unique(ans.begin(), ans.end()), ans.end()); // 进行去重
ans.insert(ans.begin(), 0); // 将离散化之后的下标从1开始
for(int i = 1;i <= m; i++) // 找到每个区间左右端点离散化之后的数据,使用新数据
{
a[i].x = get(a[i].x);
a[i].y = get(a[i].y);
}
for(int i = 0;i < 2 * N; i++) fa[i] = i; // 初始化集合,每一个元素在不同的集合中
n = ans.size(); // 每个扩展域的范围
for(int i = 1; i <= m; i++) // 开始遍历每一个回答,判断左右端点集合中的关系
{
int x = a[i].x, y = a[i].y;
string op = a[i].op;
if(op == "even") // 有偶数个1
{
// 只需要判断一种情况就可,因为他们的关系是对称的
if(find(x) == find(y + n)) // x为偶数的集合中,存在y为奇数的关系,矛盾
{
cout << i - 1 << endl;
return 0;
}
// x与y的奇偶性相同
merge(x, y); // 将x为偶数,y为偶数放在一个集合中
merge(x + n, y + n); // 将x为奇数,y为奇数放在一个集合中
}
else // 有奇数个1,那么x和y的奇偶性不同
{
if(find(x) == find(y)) // x为偶数的集合中,存在y为偶数的关系,矛盾
{
cout << i - 1 << endl;
return 0;
}
merge(x, y + n); // 将x为偶数,y为奇数放在一个集合中
merge(x + n, y); // 将x为奇数,y为偶数放在一个集合中
}
}
cout << m << endl;
return 0;
}权值并查集
每一个区间的奇偶性有两种情况,奇数或者偶数 我们可以维护集合中每个区间的关系,这个关系可以用集合中的子区间到祖宗区间的距离来表示,因为有两种情况,所以当距离d[i] % 2 == 0时,当前区间的奇偶性和祖宗元素的奇偶性相同,d[i] % 2 ==1时,当前区间的奇偶性和祖宗元素的奇偶性不同 每一个集合中的区间相对于祖宗区间的奇偶性是已知的,所以集合中所有区间的奇偶性关系都是已知的 代码实现
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int fa[N]; // 初始化每一个集合都是独立的
int d[N]; // 集合中子区间到祖宗区间的距离,可以判断奇偶关系
vector<int> ans; // 离散化数组
int n, m;
struct node // 存储每一个回答
{
int x, y;
string op;
}a[N];
int get(int u) // 二分查找进行离散化
{
int l = 0, r = ans.size();
while(l + 1 != r)
{
int mid = l + r >> 1;
if(ans[mid] < u) l = mid;
else r = mid;
}
return r;
}
int find(int u) // 找到当前区间的祖宗区间,并进行路径压缩和更新到祖宗区间的距离
{
if(fa[u] != u)
{
int t = find(fa[u]);
d[u] += d[fa[u]];
fa[u] = t;
}
return fa[u];
}
int main()
{
cin >> n >> m;
for(int i = 1;i <= m; i++)
{
cin >> a[i].x >> a[i].y >> a[i].op;
a[i].x--;
ans.push_back(a[i].x);
ans.push_back(a[i].y);
}
sort(ans.begin(), ans.end());
ans.erase(unique(ans.begin(), ans.end()), ans.end());
ans.insert(ans.begin(), 0);
for(int i = 1; i <= m; i++)
{
a[i].x = get(a[i].x);
a[i].y = get(a[i].y);
}
for(int i = 1; i <= ans.size(); i++) fa[i] = i;
for(int i = 1;i <= m; i++)
{
int fx = find(a[i].x), fy = find(a[i].y);
string op = a[i].op;
if(op == "even")
{
if(fx != fy)
{
d[fx] = d[a[i].x] ^ d[a[i].y];
fa[fx] = fy;
}
else
{
if((d[a[i].x] + d[a[i].y]) % 2 != 0)
{
cout << i - 1 << endl;
return 0;
}
}
}
else
{
if(fx != fy)
{
d[fx] = d[a[i].x] ^ d[a[i].y] ^ 1;
fa[fx] = fy;
}
else
{
if((d[a[i].x] + d[a[i].y]) % 2 == 0)
{
cout << i - 1 << endl;
return 0;
}
}
}
}
cout << m << endl;
return 0;
}