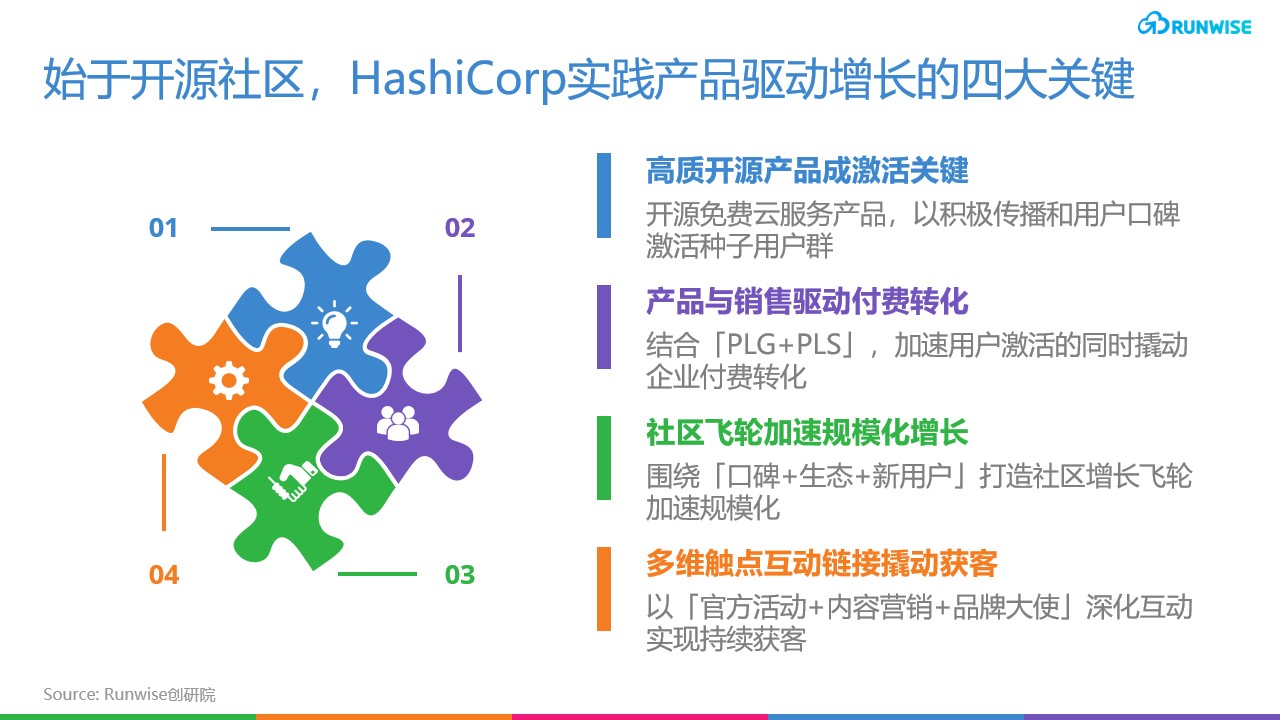
坐标系下的运动旋量转换
文章目录
- 坐标系下的运动旋量转换
- 前言
- 一、运动旋量
- 物体运动旋量
- 空间运动旋量
- 二、伴随变换矩阵
- 三、坐标系下运动旋量的转换
- 四、力旋量
- 五、总结
- 参考资料
前言
对于刚体而言,其角速度可以写为 ω ^ θ ˙ \hat {\omega} \dot \theta ω^θ˙,其中, ω ^ \hat\omega ω^为单位转轴, θ ˙ \dot \theta θ˙为绕着转轴转动的角速度大小。运动旋量则用来描述物体角速度与线速度的组合。由于在机器人学中,运动旋量可能需要描述在不同坐标系之下,本文参考凯文·M.林奇的《现代机器人学》,对运动旋量概念与坐标系下的运动旋量转换进行梳理与总结,便于自己后续回忆。
一、运动旋量
首先,定义有单位螺旋轴
S
=
(
ω
,
v
x
,
v
y
,
v
z
)
(
ω
=
1
)
S=(\omega,v_x,v_y,v_z)(\omega=1)
S=(ω,vx,vy,vz)(ω=1),利用旋转速度
θ
˙
\dot\theta
θ˙与之相乘,由此可得运动旋量
V
=
S
θ
˙
V=S\dot\theta
V=Sθ˙。这里注意:通过绕螺旋轴
S
S
S转动
θ
\theta
θ角的位移与以速度
θ
˙
=
θ
\dot\theta=\theta
θ˙=θ绕螺旋轴
S
S
S转动单位时间完全相等,因此,
V
=
S
θ
˙
V=S\dot\theta
V=Sθ˙可同样看作为指数坐标(刚体转动的指数坐标,可以等效为单位转轴
ω
^
(
ω
^
∈
R
3
,
∣
∣
ω
^
∣
∣
=
1
)
\hat\omega(\hat\omega\in R^3,||\hat\omega||=1)
ω^(ω^∈R3,∣∣ω^∣∣=1))与绕该轴线的转角
θ
∈
R
\theta\in R
θ∈R。

在对运动旋量有了大致了解以后,正式进入正题,即何为物体运动旋量、何为空间运动旋量。
物体运动旋量
首先,用
{
s
}
\{s\}
{s}与
{
b
}
\{b\}
{b}分别描述固定(空间)坐标系和移动(物体)坐标系。则有
T
s
b
(
t
)
=
[
R
(
t
)
p
(
t
)
0
1
]
T_{sb}(t)=\begin{bmatrix} R(t) & p(t) \\ \pmb0 & 1 \end{bmatrix}
Tsb(t)=[R(t)0p(t)1]
其中,
T
s
b
T_{sb}
Tsb表示从空间坐标系到物体坐标系的转换集合矩阵,后续可用
T
T
T代替。令
T
−
1
T
˙
T^{-1}\dot T
T−1T˙,则有
T
−
1
T
˙
=
[
R
T
−
R
T
p
0
1
]
[
R
˙
p
˙
0
0
]
=
[
R
T
R
˙
R
T
p
˙
0
1
]
T^{-1}\dot T=\begin{bmatrix} R^T & -R^Tp \\ \pmb0 & 1 \end{bmatrix}\begin{bmatrix} \dot R & \dot p \\ \pmb0 & 0 \end{bmatrix}=\begin{bmatrix} R^T\dot R & R^T\dot p \\ \pmb0 & 1 \end{bmatrix}
T−1T˙=[RT0−RTp1][R˙0p˙0]=[RTR˙0RTp˙1]
其中,
R
T
R
˙
=
R
−
1
R
˙
=
[
ω
b
]
R^T\dot R=R^{-1}\dot R=[\omega_b]
RTR˙=R−1R˙=[ωb],这里的
[
ω
b
]
[\omega_b]
[ωb]即为物体坐标系
{
b
}
\{b\}
{b}下的刚体角速度的反对称矩阵,
[
∗
]
[*]
[∗]符号代表
∗
*
∗的反对称矩阵。具体证明过程可参考书籍,这里不再展开。同理,
p
˙
\dot p
p˙代表坐标系
{
s
}
\{s\}
{s}中描述的
{
b
}
\{b\}
{b}的原点的线速度,因此,
R
T
p
˙
=
R
−
1
p
˙
=
v
b
R^T\dot p=R^{-1}\dot p=v_b
RTp˙=R−1p˙=vb则为在物体坐标系
{
b
}
\{b\}
{b}中描述
{
s
}
\{s\}
{s}的原点的线速度。可进一步阐述为:
T
−
1
T
˙
T^{-1}\dot T
T−1T˙表示动坐标系相对于当前与其瞬时重合的静坐标系
{
b
}
\{b\}
{b}的线速度与角速度。
构造六维向量
V
b
=
[
ω
b
v
b
]
V_b=\begin{bmatrix} \omega_b \\ v_b \end{bmatrix}
Vb=[ωbvb],定义其为物体坐标系中的速度,简称为物体运动旋量。写为矩阵形式为
T
−
1
T
˙
=
[
V
b
]
=
[
[
ω
b
]
v
b
0
1
]
∈
s
e
(
3
)
T^{-1}\dot T=[V_b]=\begin{bmatrix} [\omega_b] & v_b \\ \pmb0 & 1 \end{bmatrix} \in se(3)
T−1T˙=[Vb]=[[ωb]0vb1]∈se(3)
这里可以注意,六维向量
V
b
V_b
Vb的反对称矩阵的撰写形式,即原部矢量
w
b
w_b
wb取反对称形式,偶部矢量不改变形式。
空间运动旋量
同理,可以推导
T
˙
T
−
1
\dot TT^{-1}
T˙T−1有
V
s
=
[
ω
s
v
s
]
∈
R
6
,
T
˙
T
−
1
=
[
V
s
]
=
[
[
w
s
]
v
s
0
1
]
∈
s
e
(
3
)
V_s=\begin{bmatrix} \omega_s \\ v_s \end{bmatrix} \in R^6, \dot TT^{-1}=[V_s]=\begin{bmatrix} [w_s] & v_s \\ \pmb0 & 1 \end{bmatrix} \in se(3)
Vs=[ωsvs]∈R6,T˙T−1=[Vs]=[[ws]0vs1]∈se(3)
此时,
V
s
V_s
Vs描述空间固定坐标系中的速度,因此被称为空间运动旋量。
二、伴随变换矩阵
在第一节中,描绘了分别在两个坐标系下的运动旋量,即
V
b
V_b
Vb与
V
s
V_s
Vs,那么,如果我们已知这两个坐标系的转换矩阵
T
s
b
=
(
R
s
b
,
p
s
b
)
∈
S
E
(
3
)
T_{sb}=(R_{sb},p_{sb})\in SE(3)
Tsb=(Rsb,psb)∈SE(3),我们是否可以对这两个运动旋量建立联系呢?答案就是伴随变换矩阵。即有
V
s
=
[
ω
s
v
s
]
=
[
A
d
T
s
b
]
V
b
=
[
R
s
b
0
[
p
s
b
]
R
s
b
R
s
b
]
[
ω
b
v
b
]
V_s=\begin{bmatrix} \omega_s \\ v_s \end{bmatrix}=[Ad_{T_{sb}}]V_b=\begin{bmatrix} R_{sb} & \pmb 0\\ [p_{sb}]R_{sb} & R_{sb} \end{bmatrix} \begin{bmatrix} \omega_b \\ v_b \end{bmatrix}
Vs=[ωsvs]=[AdTsb]Vb=[Rsb[psb]Rsb0Rsb][ωbvb]
其中,
[
A
d
T
s
b
]
=
[
R
s
b
0
[
p
s
b
]
R
s
b
R
s
b
]
∈
R
6
×
6
[Ad_{T_{sb}}]=\begin{bmatrix} R_{sb} & \pmb 0\\ [p_{sb}]R_{sb} & R_{sb} \end{bmatrix} \in R^{6\times6}
[AdTsb]=[Rsb[psb]Rsb0Rsb]∈R6×6即为该伴随变换矩阵。
将其化为矩阵形式,则有
[
V
s
]
=
T
s
b
[
V
b
]
T
−
1
[V_s]=T_{sb}[V_b]T^{-1}
[Vs]=Tsb[Vb]T−1
三、坐标系下运动旋量的转换
结合第二、三节内容,即可总结空间、物体坐标系下运动旋量的转换关系:
T
s
b
(
t
)
=
T
(
t
)
=
[
R
(
t
)
p
(
t
)
0
1
]
∈
S
E
(
3
)
T_{sb}(t)=T(t)=\begin{bmatrix} R(t) & p(t)\\ \pmb0 & 1 \end{bmatrix}\in SE(3)
Tsb(t)=T(t)=[R(t)0p(t)1]∈SE(3)仍表示固定坐标系
{
s
}
\{s\}
{s}到物体坐标系
{
b
}
\{b\}
{b}的位姿转换矩阵(这里的
S
E
(
3
)
SE(3)
SE(3)即为一种特殊李群)。则有
物体运动旋量(body twist)
T
−
1
T
˙
=
[
V
b
]
=
[
[
ω
b
]
v
b
0
1
]
∈
s
e
(
3
)
T^{-1}\dot T=[V_b]=\begin{bmatrix} [\omega_b] & v_b \\ \pmb0 & 1 \end{bmatrix} \in se(3)
T−1T˙=[Vb]=[[ωb]0vb1]∈se(3)
空间运动旋量(spatial twist)
T
˙
T
−
1
=
[
V
s
]
=
[
[
ω
s
]
v
s
0
1
]
∈
s
e
(
3
)
\dot TT^{-1}=[V_s]=\begin{bmatrix} [\omega_s] & v_s \\ \pmb0 & 1 \end{bmatrix} \in se(3)
T˙T−1=[Vs]=[[ωs]0vs1]∈se(3)
运动旋量
V
b
V_b
Vb与
V
s
V_s
Vs存在关系为
V
s
=
[
ω
s
v
s
]
=
[
R
s
b
0
[
p
s
b
]
R
s
b
R
s
b
]
[
ω
b
v
b
]
=
[
A
d
T
s
b
]
V
b
V_s=\begin{bmatrix} \omega_s \\ v_s \end{bmatrix}=\begin{bmatrix} R_{sb} & \pmb 0\\ [p_{sb}]R_{sb} & R_{sb} \end{bmatrix} \begin{bmatrix} \omega_b \\ v_b \end{bmatrix}=[Ad_{T_{sb}}]V_b
Vs=[ωsvs]=[Rsb[psb]Rsb0Rsb][ωbvb]=[AdTsb]Vb
V
b
=
[
ω
b
v
b
]
=
[
R
s
b
T
0
−
R
s
b
T
[
p
s
b
]
R
s
b
T
]
[
ω
s
v
s
]
=
[
A
d
T
s
b
]
V
s
V_b=\begin{bmatrix} \omega_b \\ v_b \end{bmatrix}=\begin{bmatrix} R_{sb}^T & \pmb 0\\ -R_{sb}^T[p_{sb}] & R_{sb}^T \end{bmatrix} \begin{bmatrix} \omega_s \\ v_s \end{bmatrix}=[Ad_{T_{sb}}]V_s
Vb=[ωbvb]=[RsbT−RsbT[psb]0RsbT][ωsvs]=[AdTsb]Vs
这里友情提示下,在《现代机器人学》第三次印刷本中,对于
V
s
V_s
Vs到
V
b
V_b
Vb的转换似乎存在小错误,不过问题不大,一般都能看出来,自行矫正即可。
四、力旋量
与运动旋量对应的,也存在着力旋量的定义。对作用于空间物体上的力矩
m
a
m_a
ma与
f
a
f_a
fa,同样可将其合成为六维的空间力的形式,其称为力旋量(wrench),在坐标系
{
a
}
\{a\}
{a}中可描述为
F
a
=
[
m
a
f
a
]
∈
R
6
F_a=\begin{bmatrix} m_a \\ f_a \end{bmatrix} \in R^6
Fa=[mafa]∈R6
如若作用于刚体的力旋量不唯一,即将其通过力旋量的六维形式直接相加即可。无力元素的力旋量则被称为纯力偶(pure moment)。
关于力旋量的转换关系,基于系统功率一定原则,最终可推导出:
F
b
=
[
A
d
T
a
b
T
]
F
a
F_b=[Ad_{T_{ab}}^T]F_a
Fb=[AdTabT]Fa
其中,
F
a
F_a
Fa与
F
b
F_b
Fb分别为坐标系
{
a
}
\{a\}
{a}与坐标系
{
b
}
\{b\}
{b}中的力旋量,
T
a
b
T_{ab}
Tab为坐标系
{
a
}
\{a\}
{a}到坐标系
{
b
}
\{b\}
{b}的转换矩阵。
五、总结
在学习运动旋量与李群李代数时,一开始感觉确实有些晦涩且难以理解,但是在反复学习时,又感觉其形式简洁且非常实用,因此在这里学习记录,供后续参考。
参考资料
【1】https://www.bilibili.com/video/BV1KV411Z7sC/?p=17&vd_source=029a7426f7a6cecb96f1969e1ce8aff7。
【2】现代机器人学:机构、规划与控制。