雷达模糊函数及MATLAB仿真

文章目录

前言
一、雷达模糊函数
二、Matlab 仿真
- 1、单脉冲模糊函数
- - ①、MATLAB 源码
  - ②、仿真结果
  - - 1）不确定函数三维图
    - 2）不确定函数的等高图
    - 3）模糊函数的三维图
    - 4）模糊函数的等高图
- 2、单脉冲多普勒频率轴上的切面
- - ①、MATLAB 源码
  - ②、仿真结果
  - - 1）单频脉冲（零延迟）的不确定函数
    - 2）单频脉冲（零延迟）的模糊度函数
- 3、LFM 信号模糊函数
- - ①、MATLAB 源码
  - ②、仿真结果
  - - 1）上调频 LFM 信号三维不确定图
    - 2）上调频 LFM 信号不确定函数等高线图
    - 3）上调频 LFM 信号三维模糊度图
    - 4）上调频 LFM 信号模糊函数等高线图
- 4、LFM 沿时间延迟轴 $\tau$ 的切面
- - ①、MATLAB 源码
  - ②、仿真结果
  - - 1）不确定函数切面图
    - 2）模糊函数切面图
- 5、相干脉冲串模糊度函数
- - ①、MATLAB 源码
  - ②、仿真结果
  - - 1）相干脉冲串的三维模糊图
    - 2）相干脉冲串的等高线图
- 6、二进制相位编码
- - ①、MATLAB 源码
  - ②、仿真结果
  - - 1）巴克码的模糊函数图
    - 2）巴克码的模糊函数切面图
    - 3）巴克码的等高线图
- 7、伪随机数编码
- - ①、MATLAB 源码
  - ②、仿真结果
  - - 1）PRN 码的模糊函数图
    - 2）PRN 码的模糊函数切面图
    - 3）PRN 码的等高线图
三、资源自取

前言

本文对雷达模糊函数的内容以思维导图的形式呈现，有关仿真部分进行了讲解实现。

一、雷达模糊函数

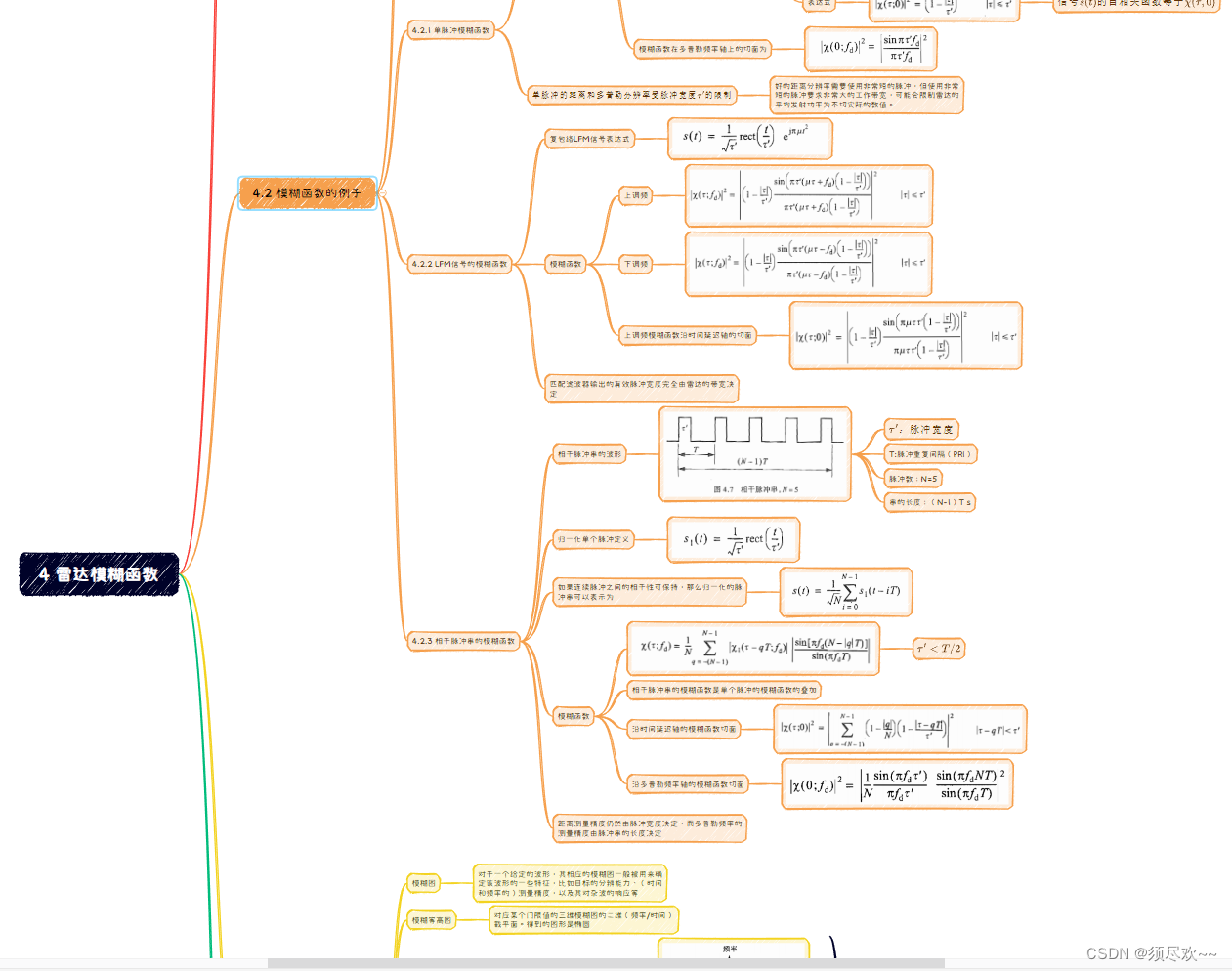
思维导图如下图所示，如有需求请到文章末尾端自取。
在这里插入图片描述

二、Matlab 仿真

1、单脉冲模糊函数

归一化的矩形脉冲定义为：
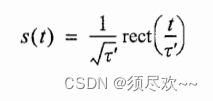
在这里插入图片描述
单脉冲不确定函数表达式

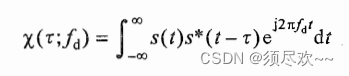
单脉冲模糊函数表达式

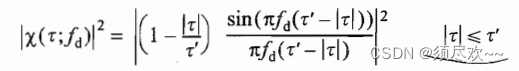
①、MATLAB 源码

single_pulse_ambg.m

function x = single_pulse_ambg (taup)
%colormap (gray(1))
eps = 0.000001;
i = 0;
taumax = 1.1 * taup;
taumin = -taumax;
for tau = taumin:.05:taumax
   i = i + 1;
   j = 0;
   for fd = -5/taup:.05:5/taup %-2.5:.05:2.5
      j = j + 1;
      val1 = 1. - abs(tau) / taup;
      val2 = pi * taup * (1.0 - abs(tau) / taup) * fd;
      x(j,i) = abs( val1 * sin(val2+eps)/(val2+eps));
   end
end

Fig4_2.m

close all
clear all
eps = 0.000001;
taup = 2.;
taumin = -1.1 * taup;
taumax = -taumin;
x = single_pulse_ambg(taup);
taux = taumin:.05:taumax;
fdy = -5/taup:.05:5/taup;
figure(1)
mesh(taux,fdy,x);
xlabel ('Delay - seconds')
ylabel ('Doppler - Hz')
zlabel ('Ambiguity function')
%colormap([.5 .5 .5])
%colormap (gray)
figure(2)
contour(taux,fdy,x);
xlabel ('Delay - seconds')
ylabel ('Doppler - Hz')
%colormap([.5 .5 .5])
%colormap (gray)
grid
y = x.^2;
figure(3)
mesh(taux,fdy,y);
xlabel ('Delay - seconds')
ylabel ('Doppler - Hz')
zlabel ('Ambiguity function')
%colormap([.5 .5 .5])
%colormap (gray)
figure(4)
contour(taux,fdy,y);
xlabel ('Delay - seconds')
ylabel ('Doppler - Hz')
%colormap([.5 .5 .5])
%colormap (gray)
grid

②、仿真结果

1）不确定函数三维图

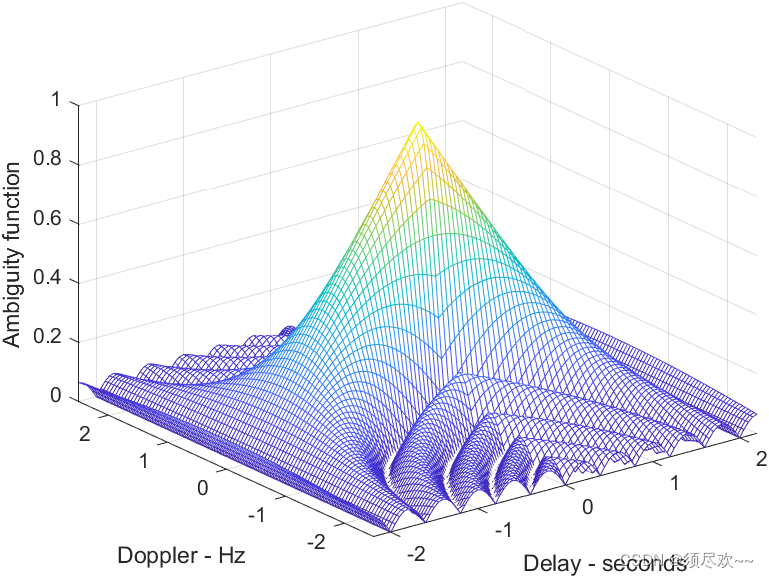
请添加图片描述

2）不确定函数的等高图

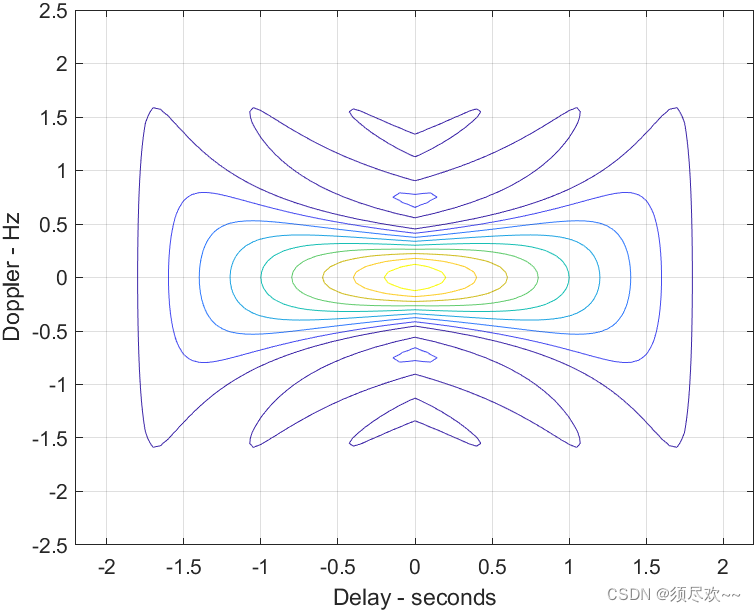
请添加图片描述

3）模糊函数的三维图

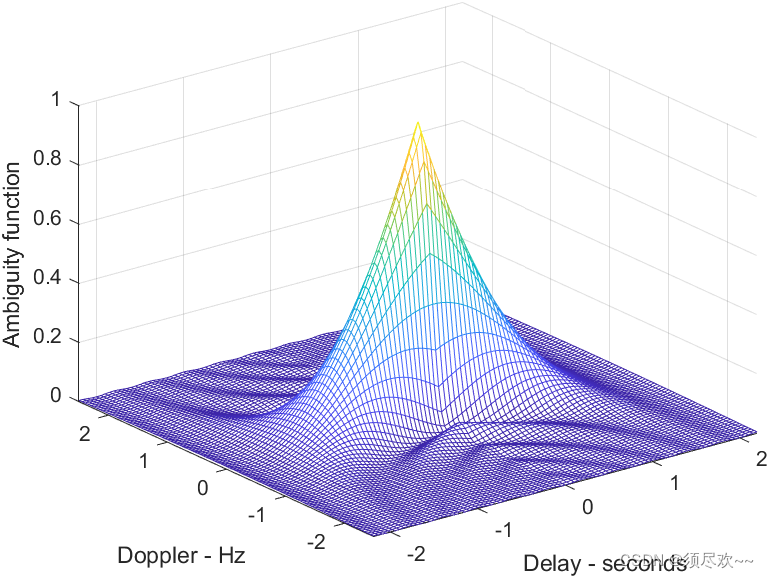
请添加图片描述

4）模糊函数的等高图

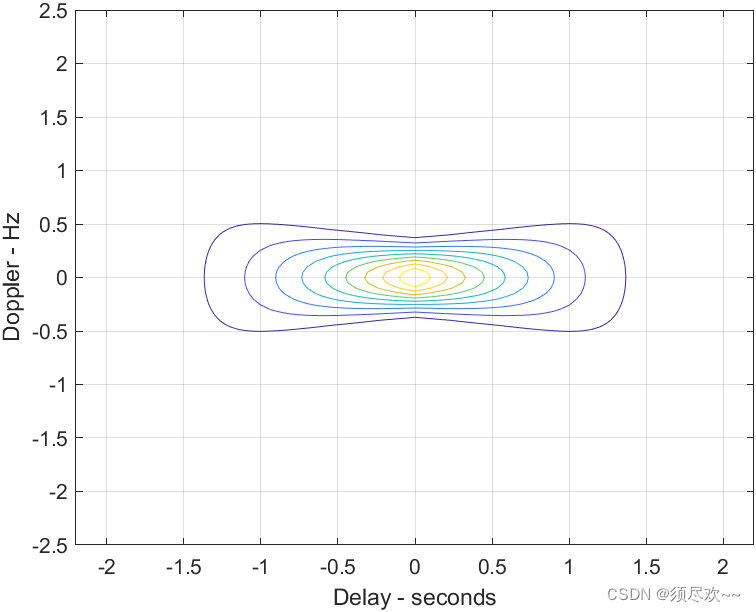
请添加图片描述

2、单脉冲多普勒频率轴上的切面

模糊函数在多普勒频率轴上的切面为：
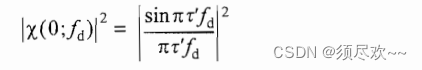
在这里插入图片描述

①、MATLAB 源码

fig4_4.m

close all
clear all
eps = 0.0001;
taup = 2.;
fd = -10./taup:.05:10./taup;
uncer = abs( sinc(taup .* fd));
ambg = uncer.^2;
plot(fd, ambg,'k')
xlabel ('Frequency - Hz')
ylabel ('Ambiguity - Volts')
grid
figure(2)
plot (fd, uncer,'k');
xlabel ('Frequency - Hz')
ylabel ('Uncertainty - Volts')
grid

②、仿真结果

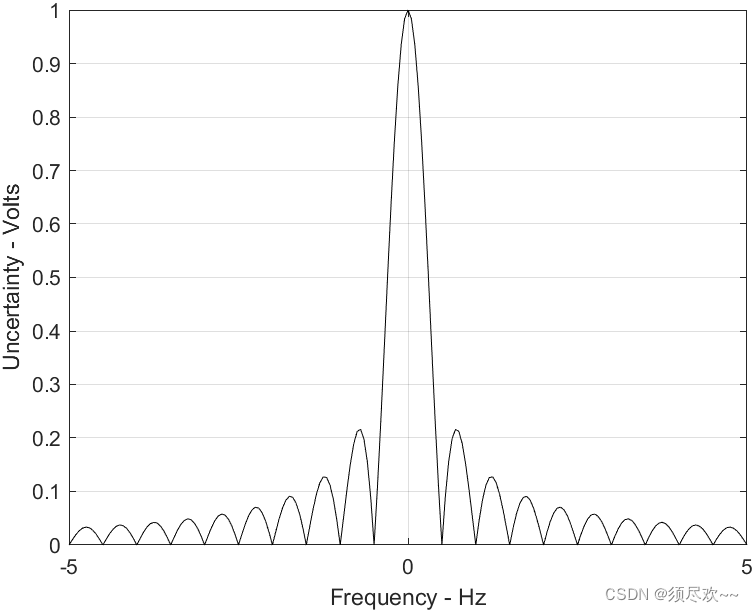
1）单频脉冲（零延迟）的不确定函数

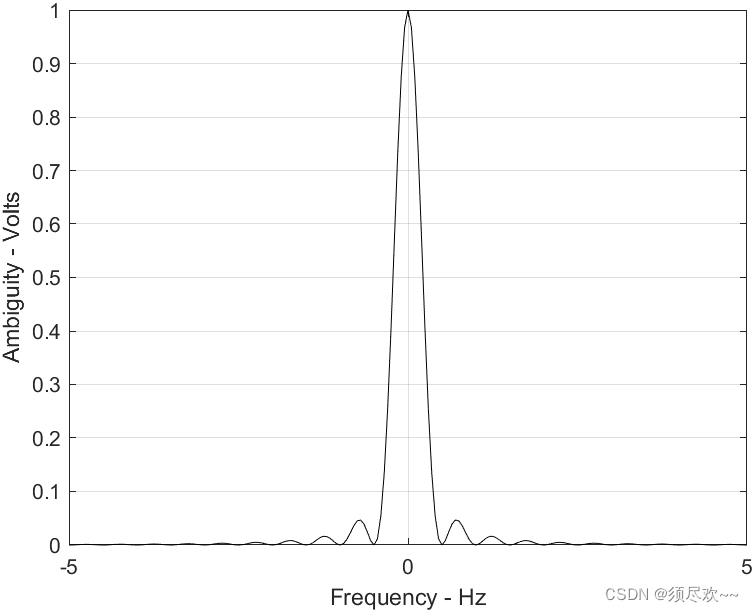
请添加图片描述

2）单频脉冲（零延迟）的模糊度函数

请添加图片描述

3、LFM 信号模糊函数

上调频 LFM 信号的模糊函数为：
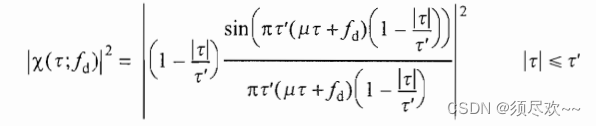
在这里插入图片描述
下调频 LFM 信号的模糊函数为：

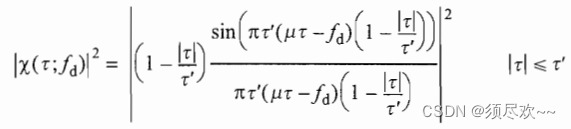
①、MATLAB 源码

lfm_ambg.m

function x = lfm_ambg(taup, b, up_down)
eps = 0.000001;
i = 0;
mu = up_down * b / 2. / taup;
delt = 2.2*taup/250;
delf = 2*b /250;
for tau = -1.1*taup:.05:1.1*taup
   i = i + 1;
   j = 0;
   for fd = -b:.05:b
      j = j + 1;
      val1 = 1. - abs(tau) / taup;
      val2 = pi * taup * (1.0 - abs(tau) / taup);
      val3 = (fd + mu * tau);
      val = val2 * val3;
      x(j,i) = abs( val1 * (sin(val+eps)/(val+eps))).^2;
   end
end

在这里插入图片描述
fig4_5.m

close all
clear all
eps = 0.0001;
taup = 1.;
b =10.;
up_down = 1.;
x = lfm_ambg(taup, b, up_down);
taux = -1.1*taup:.05:1.1*taup;
fdy = -b:.05:b;
figure(1)
mesh(taux,fdy,x)
xlabel ('Delay - seconds')
ylabel ('Doppler - Hz')
zlabel ('Ambiguity function')
figure(2)
contour(taux,fdy,x)
xlabel ('Delay - seconds')
ylabel ('Doppler - Hz')
y = sqrt(x);
figure(3)
mesh(taux,fdy,y)
xlabel ('Delay - seconds')
ylabel ('Doppler - Hz')
zlabel ('Uncertainty function')
figure(4)
contour(taux,fdy,y)
xlabel ('Delay - seconds')
ylabel ('Doppler - Hz')

②、仿真结果

在这里插入图片描述

1）上调频 LFM 信号三维不确定图

脉宽 1s，带宽 10Hz
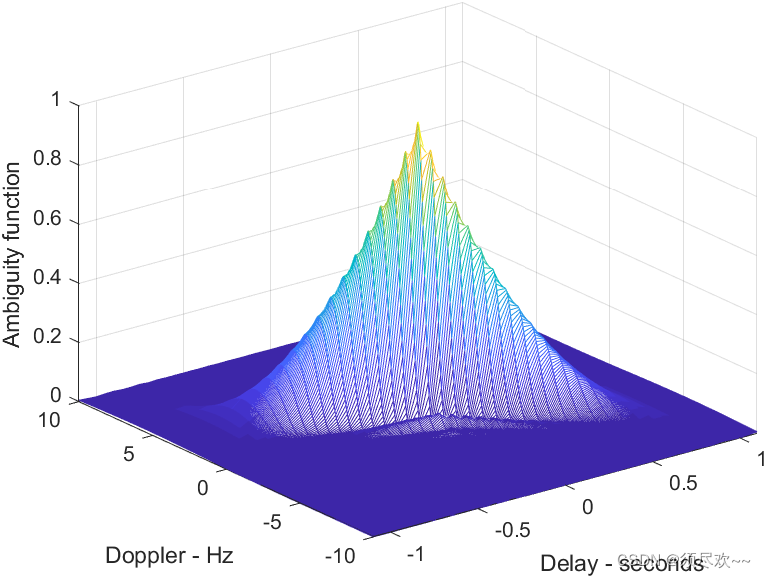
请添加图片描述

2）上调频 LFM 信号不确定函数等高线图

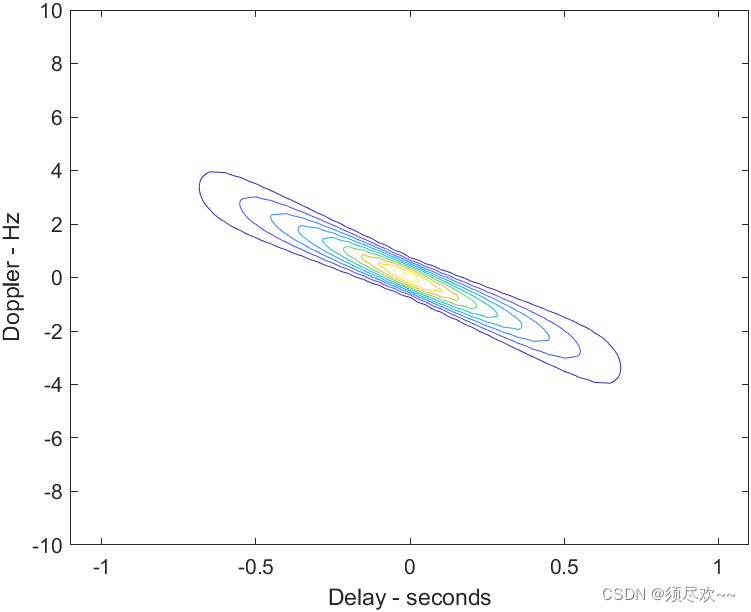
请添加图片描述

3）上调频 LFM 信号三维模糊度图

脉宽 1s，带宽 10Hz
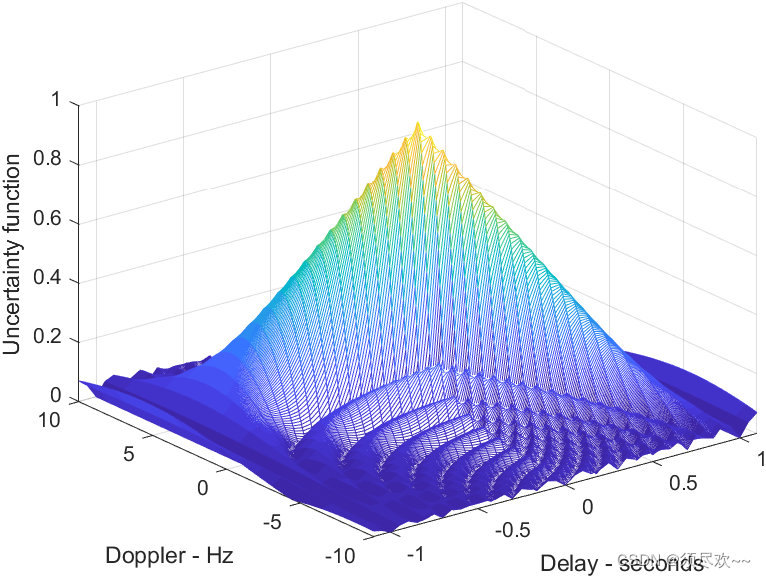
在这里插入图片描述

4）上调频 LFM 信号模糊函数等高线图

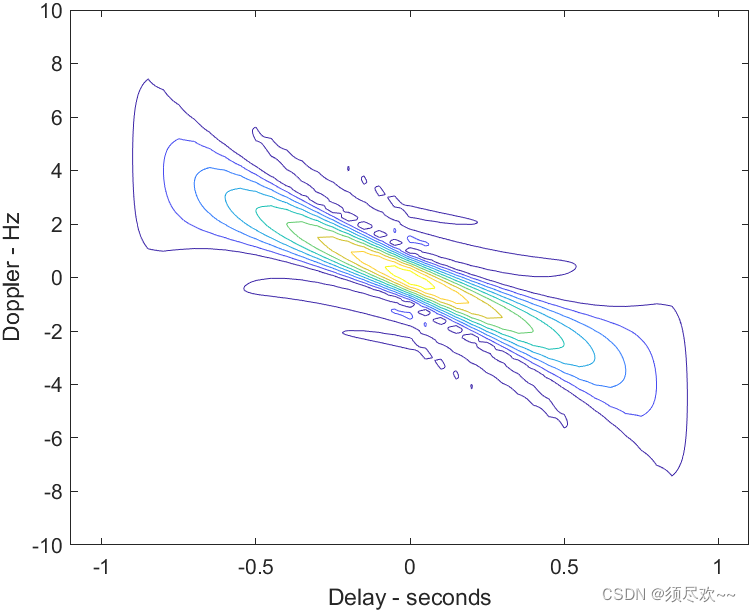
在这里插入图片描述

4、LFM 沿时间延迟轴 $\tau$ 的切面

上调频模糊函数沿时间延迟轴 $\tau$ 的切面为：
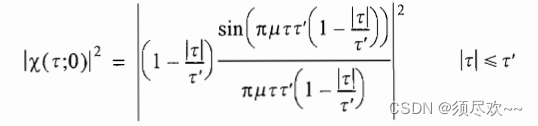
在这里插入图片描述

①、MATLAB 源码

close all
clear all
taup = 1;
b =20.;
up_down = 1.;
taux = -1.5*taup:.01:1.5*taup;
fd = 0.;
mu = up_down * b / 2. / taup;
ii = 0.;
for tau = -1.5*taup:.01:1.5*taup
   ii = ii + 1;
   val1 = 1. - abs(tau) / taup;
   val2 = pi * taup * (1.0 - abs(tau) / taup);
   val3 = (fd + mu * tau);
   val = val2 * val3;
   x(ii) = abs( val1 * (sin(val+eps)/(val+eps)));
end
figure(1)
plot(taux,x)
grid
xlabel ('Delay - seconds')
ylabel ('Uncertainty')
figure(2)
plot(taux,x.^2)
grid
xlabel ('Delay - seconds')
ylabel ('Ambiguity')

②、仿真结果

1）不确定函数切面图

LFM 脉冲（ $\tau'=1,b=20$ ）的零多普勒不确定函数

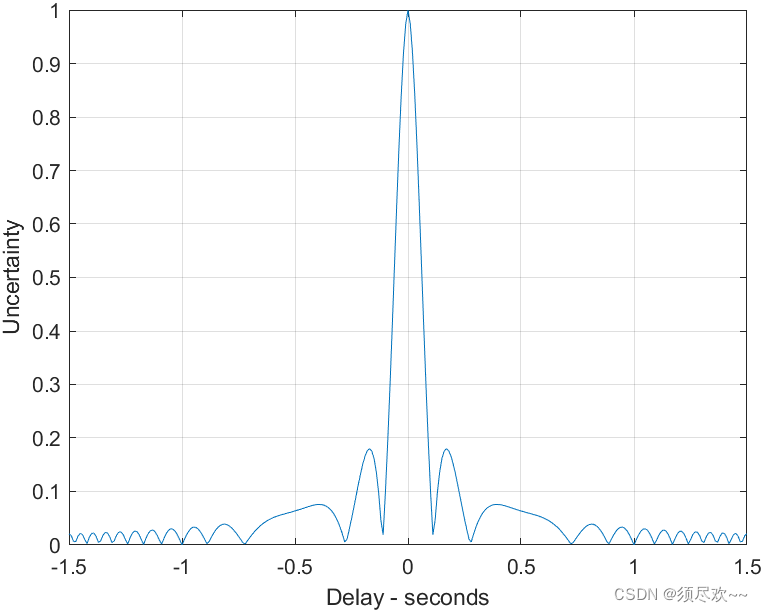
请添加图片描述
注意到 LFM 信号模糊函数沿多普勒频率轴的切面是与单脉冲类似的，因为脉冲形状没有发生改变（只是增加了频率调制）。然而，沿时间延迟轴的切面变化显著，与没有调制脉冲的切面图相比窄了很多，第一个零点位于：
$\tau_{n1}\approx 1/B$
这表明匹配滤波器输出的有效脉冲宽度由雷达的带宽决定。

2）模糊函数切面图

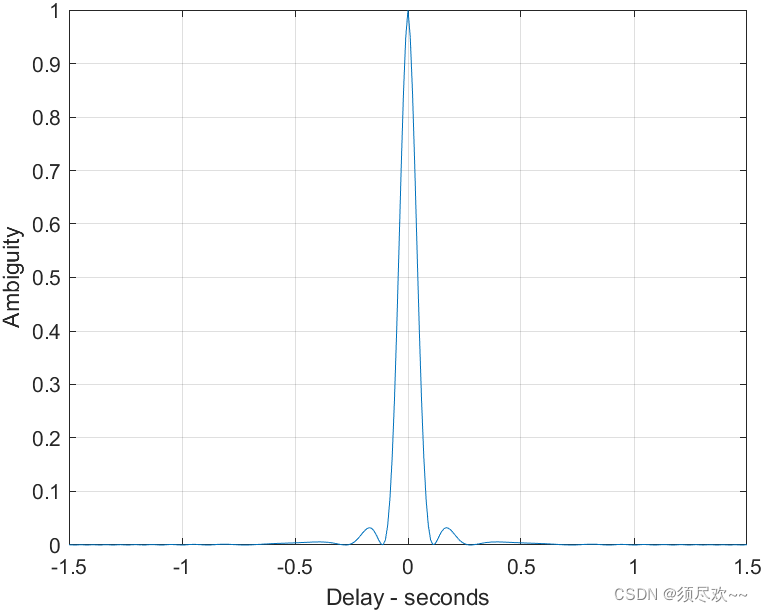
请添加图片描述

5、相干脉冲串模糊度函数

相干脉冲串的模糊函数。对于 $\tau'<T/2$ ：
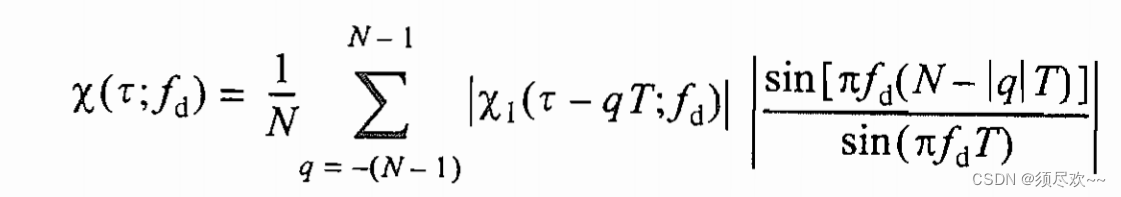
在这里插入图片描述
沿时间延迟轴的模糊函数切面：

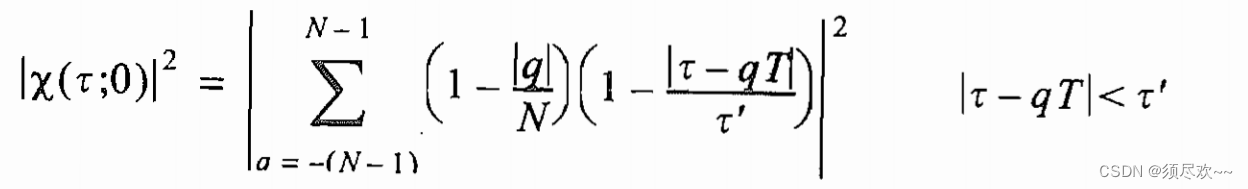
沿多普勒频率轴的模糊函数切面：

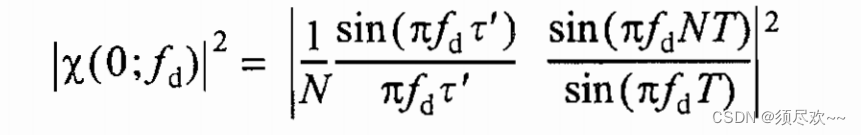
①、MATLAB 源码

train_ambg.m

function x = train_ambg (taup, n, pri)
if( taup > pri / 2.)
   'ERROR. Pulse width must be less than the PRI/2.'
   return
end
gap = pri - 2.*taup;
eps = 0.000001;
b = 1. / taup;
ii = 0.;
for q = -(n-1):1:n-1
   tauo = q - taup ;
   index = -1.;
   for tau1 = tauo:0.0533:tauo+gap+2.*taup
      index = index + 1;
      tau = -taup + index*.0533;
      ii = ii + 1;
      j = 0.;
      for fd = -b:.0533:b
         j = j + 1;
         if (abs(tau) <= taup)
            val1 = 1. -abs(tau) / taup;
            val2 = pi * taup * fd * (1.0 - abs(tau) / taup);
            val3 = abs(val1 * sin(val2+eps) /(val2+eps)); 
            val4 = abs((sin(pi*fd*(n-abs(q))*pri+eps))/(sin(pi*fd*pri+eps)));
            x(j,ii)=  val3 * val4 / n;
         else
            x(j,ii) = 0.;
         end
      end
   end
end

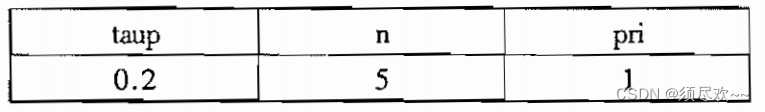
在这里插入图片描述

fig4_8.m

close all
clear all
taup =0.2;
pri=1;
n=5;
x = train_ambg (taup, n, pri);
figure(1)
mesh(x)
xlabel ('Delay - seconds')
ylabel ('Doppler - Hz')
zlabel ('Ambiguity function')
figure(2)
contour(x);
xlabel ('Delay - seconds')
ylabel ('Doppler - Hz')

②、仿真结果

1）相干脉冲串的三维模糊图

5个脉冲等幅相干串的三维模糊图，脉冲宽度为 0.2s，PRI 为 1s，N=5
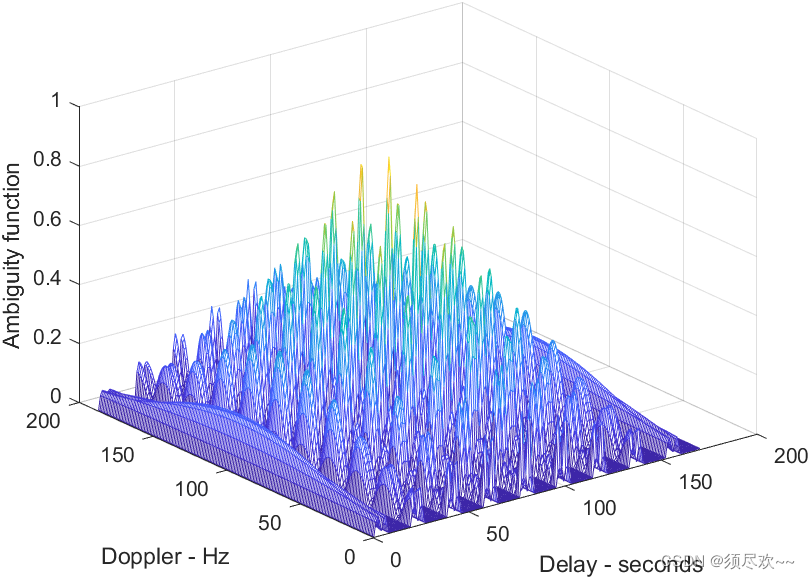
请添加图片描述

2）相干脉冲串的等高线图

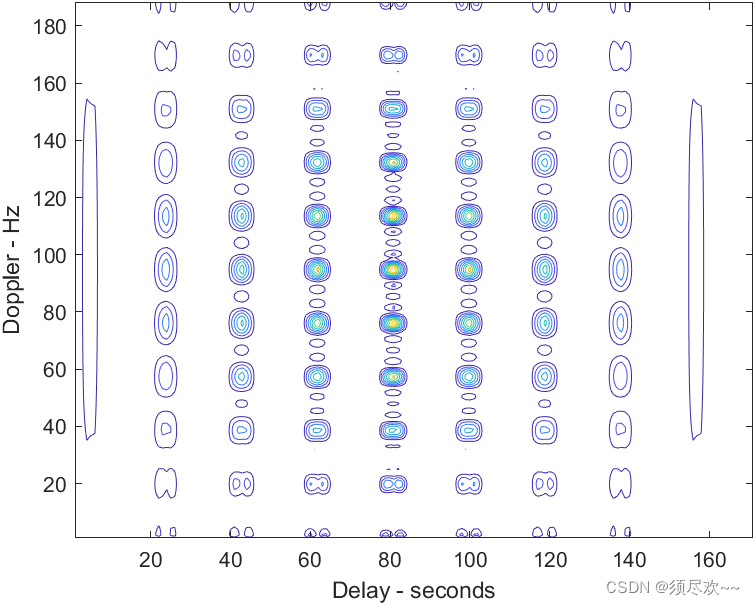
请添加图片描述

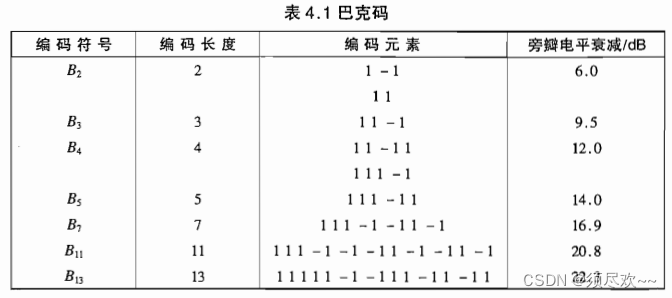
6、二进制相位编码

巴克码是二进制相位编码中的一族，它产生的压缩后的波形具有恒等于单位值的旁瓣电平。
在这里插入图片描述
相位编码的通用形式：

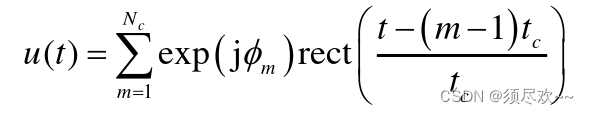
巴克码自相关函数：

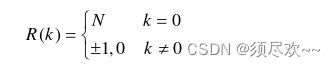
①、MATLAB 源码

Barker_ambig.m

function [ambig] = barker_ambig(uinput)
% Compute and plot the ambiguity function for a Barker code
%Compute the ambiguity function
% by utilizing the FFT through combining multiple range cuts
N = size(uinput,2);
tau = N;
Barker_code = uinput;
samp_num = size(Barker_code,2) *10;
n = ceil(log(samp_num) / log(2));
nfft = 2^n;
u(1:nfft) = 0;
j = 0;
for index = 1:10:samp_num
    index;
    j = j+1;
    u(index:index+10-1) = Barker_code(j);
end
v = u;
delay = linspace(-tau, tau, nfft);
freq_del = 12 / tau /100;
j = 0;
vfft = fft(v,nfft);
for freq = -6/tau:freq_del:6/tau;
    j = j+1;
    exf = exp(sqrt(-1) * 2. * pi * freq .* delay);
    u_times_exf = u .* exf;
    ufft = fft(u_times_exf,nfft);
    prod = ufft .* conj(vfft);
    ambig(:,j) = fftshift(abs(ifft(prod))');
end
freq = -6/tau:freq_del:6/tau;
delay = linspace(-N,N,nfft);
figure (1)
mesh(freq,delay,ambig ./ max(max(ambig)))
%colormap([.5 .5 .5])
%colormap(gray)
axis tight
xlabel('frequency')
ylabel('delay')
zlabel('ambiguity function')
figure (2)
value = 10 * N ;
plot(delay,ambig(:,51)/value,'k')
xlabel('delay')
ylabel('normalized amibiguity cut for f=0')
grid
axis tight
figure (3)
contour(freq,delay,ambig ./ max(max(ambig)))
%colormap([.5 .5 .5])
%colormap (gray)
xlabel('frequency')
ylabel('delay')
grid on

test.m

close all
clear all
u = [1 1 1 1 1 -1 -1 1 1 -1 1 -1 1];
x = Barker_ambig(u);

程序中举例的是长度为 13 的巴克码

②、仿真结果

1）巴克码的模糊函数图

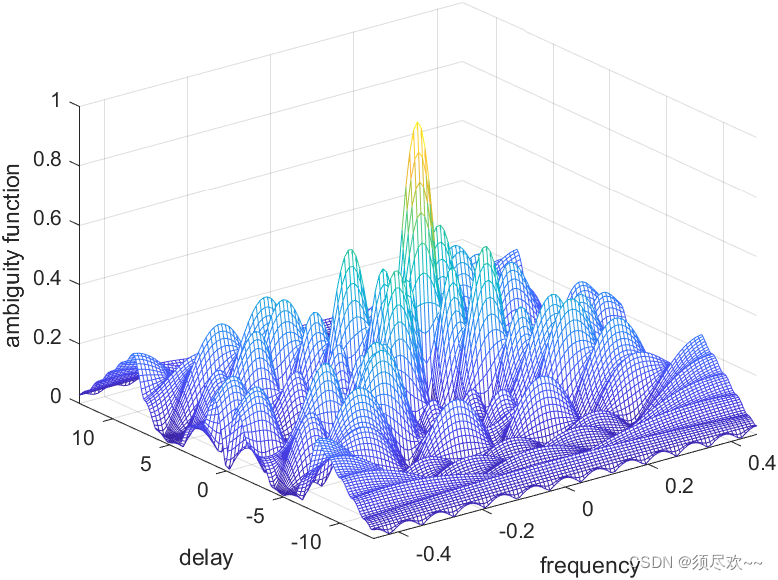
请添加图片描述

2）巴克码的模糊函数切面图

巴克码的零多普勒模糊函数图
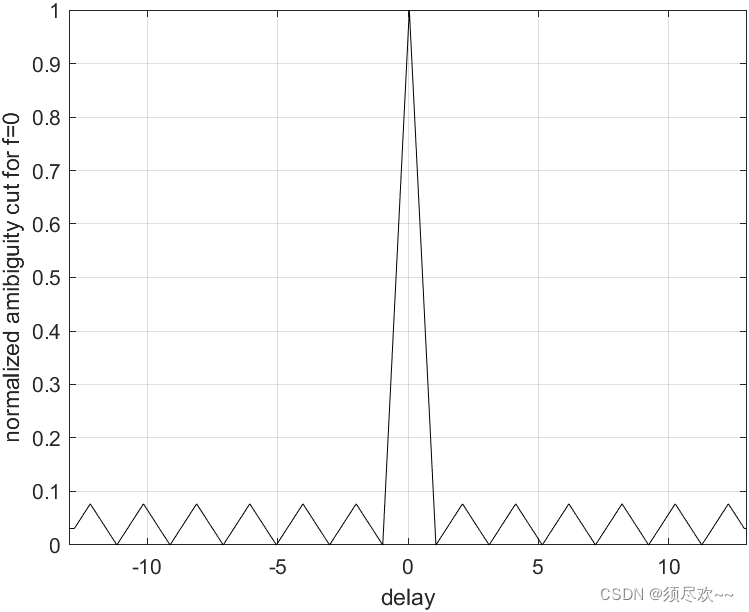
请添加图片描述

3）巴克码的等高线图

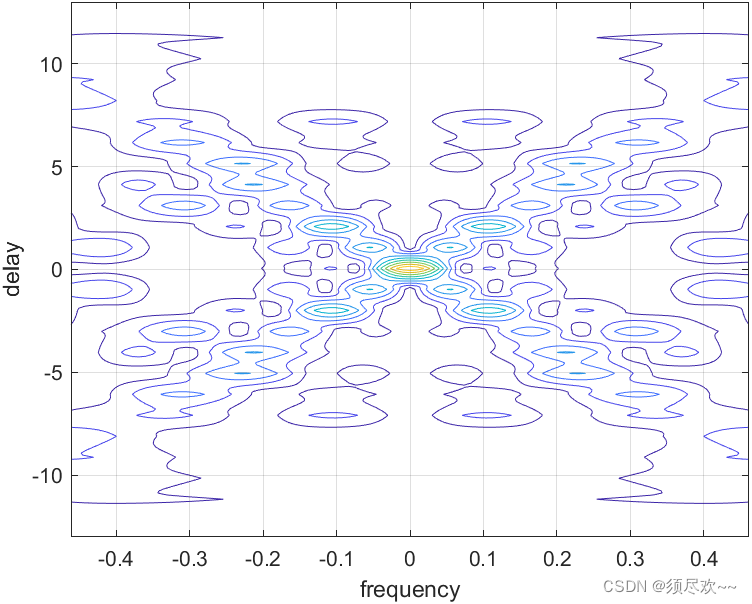
请添加图片描述

7、伪随机数编码

伪随机数（PRN）编码也称为最大长度序列（MLS）码。

①、MATLAB 源码

prn_ambig.m

function [ambig] = prn_ambig(uinput)
% Compute and plot the ambiguity function for a PRN code
% Compute the ambiguity function by utilizing the FFT 
% through combining multiple range cuts

N = size(uinput,2);
tau = N;
PRN = uinput;
samp_num = size(PRN,2) * 10;
n = ceil(log(samp_num) / log(2));
nfft = 2^n;
u(1:nfft) = 0;
j = 0;
for index = 1:10:samp_num
    index;
    j = j+1;
    u(index:index+10-1) = PRN(j);
end
% set-up the array v
v = u;
delay = linspace(0,5*tau,nfft);
freq_del = 8 / tau /100;
j = 0;
vfft = fft(v,nfft);
for freq = -4/tau:freq_del:4/tau;
    j = j+1;
    exf = exp(sqrt(-1) * 2. * pi * freq .* delay);
    u_times_exf = u .* exf;
    ufft = fft(u_times_exf,nfft);
    prod = ufft .* conj(vfft);
    ambig(:,j) = fftshift(abs(ifft(prod))');
end
freq = -4/tau:freq_del:4/tau;
delay = linspace(-N,N,nfft);
figure(1)
mesh(freq,delay,ambig ./ max(max(ambig)))
% colormap([.5 .5 .5])
% colormap(gray)
axis tight
xlabel('frequency')
ylabel('delay')
zlabel('ambiguity function a PRN code')
figure(2)
plot(delay,ambig(:,51)/(max(max(ambig))),'k')
xlabel('delay')
ylabel('normalized amibiguity cut for f=0')
grid
axis tight
figure(3)
contour(freq,delay,ambig ./ max(max(ambig)))
axis tight
% colormap([.5 .5 .5])
% colormap(gray)
xlabel('frequency')
ylabel('delay')

test.m

close all
clear all
u_31 = [1 -1 -1 -1 -1 1 -1 1 -1 1 1 1 -1 1 1 -1 -1 -1 1 1 1 1 1 -1 -1 1 1 -1 1 -1 -1];
x = prn_ambig(u_31);

u_31 是一个向量，它定义了以 “1” 和 “-1” 表示的输入最大长度码（序列）

②、仿真结果

1）PRN 码的模糊函数图

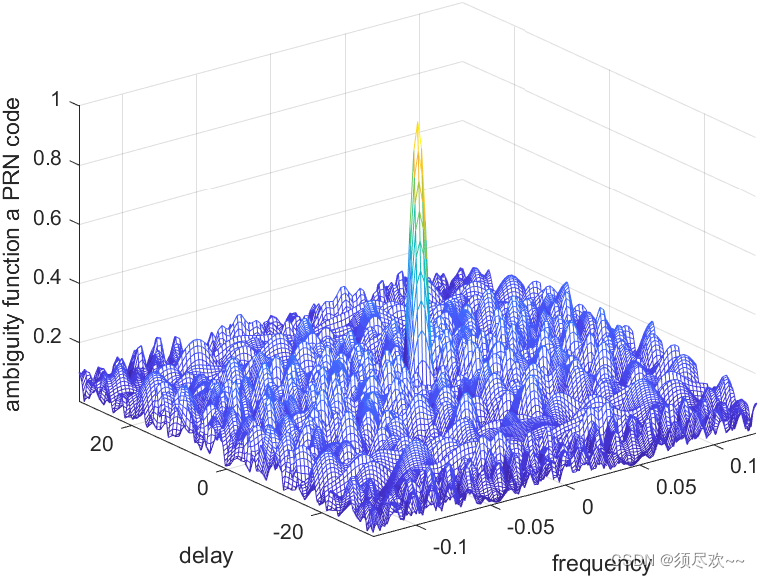
请添加图片描述

2）PRN 码的模糊函数切面图

PRN 码的零多普勒模糊函数图
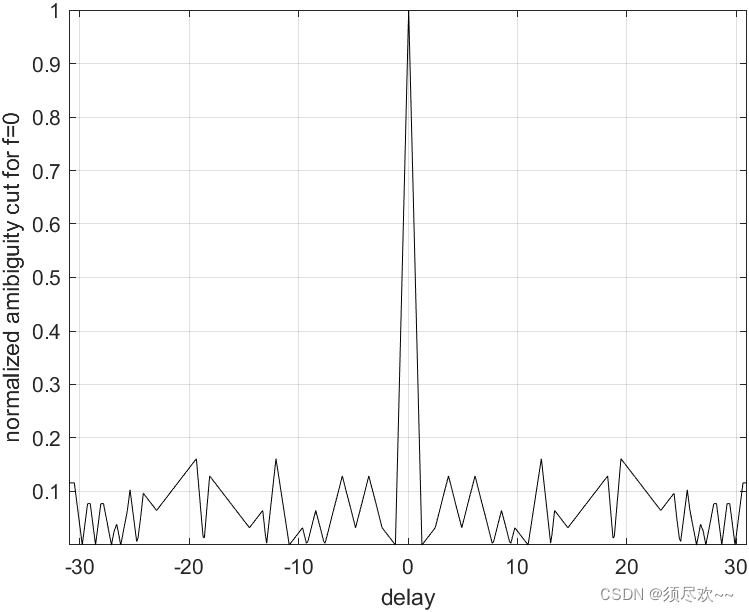
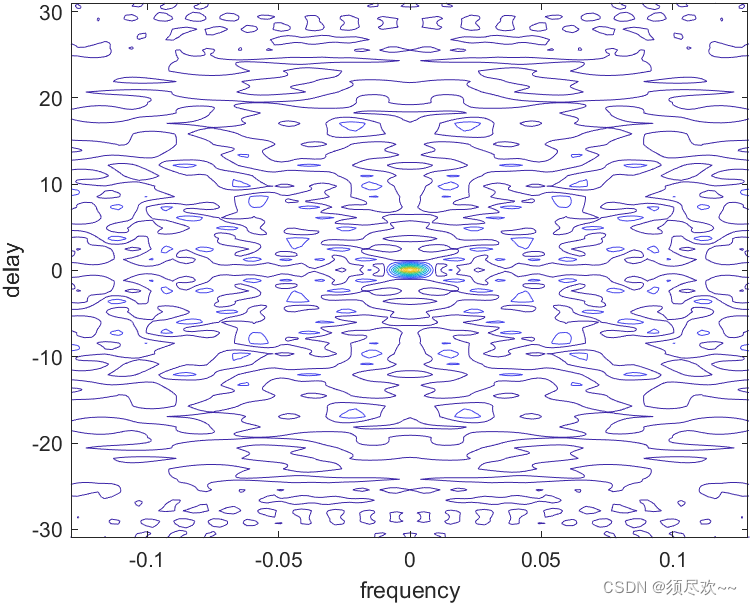
请添加图片描述

3）PRN 码的等高线图

请添加图片描述

三、资源自取

雷达模糊度函数思维导图

我的qq：2442391036，欢迎交流！