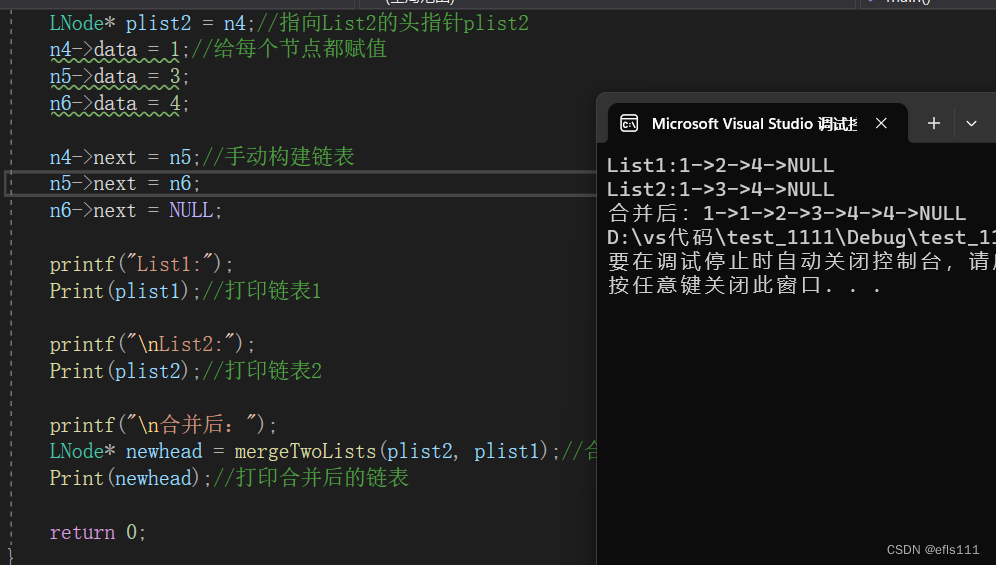
1. 简述

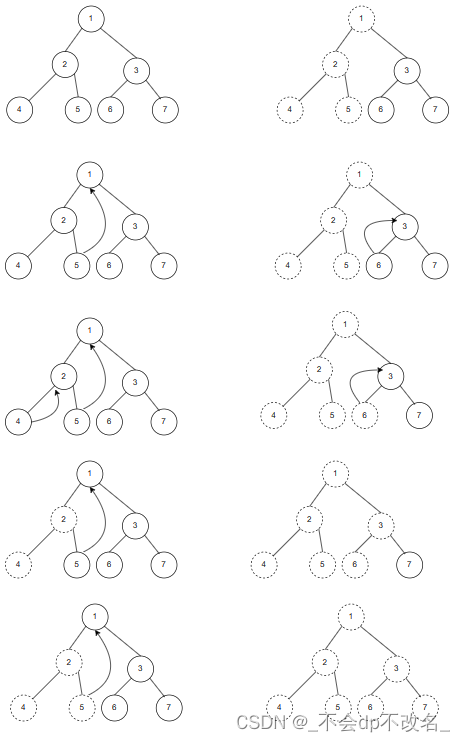
morris遍历是不借助栈空间实现二叉树遍历的一种方法。

其核心思想是，利用当前节点左子树的最右叶子节点当索引节点。

即中序遍历的前驱节点。

第一次遍历根节点的时候，找到该节点，将该节点右儿子指向根节点。

第二次回到该节点时，将前驱标记给删除掉。

2. 图解过程

3. 代码实现

前序遍历与中序遍历都符合前驱的建立过程，而后序则复杂些。

后序遍历加入的是左子树根节点到左子树最右子节点的所有节点的逆序。

所以对于后序遍历来说，过程是这样的。

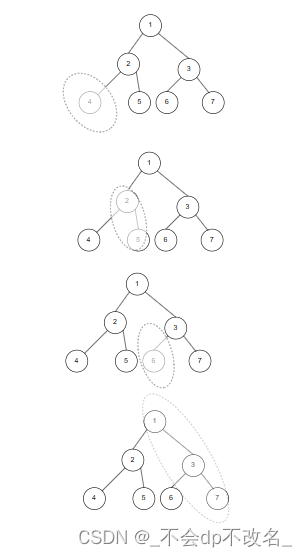
3.1 前序遍历

void PreOrderMorris(node *root)
{

    while ( root ) {

        if ( root->left != NULL) {
            node *preNode = root->left;

            while ( preNode->right != nullptr && preNode->right != root)
                preNode = preNode->right;
            if ( preNode->right == nullptr) {
                preNode->right = root;
                std::cout << root->val << ' ';
                root = root->left;
            }
            else {
                preNode->right = nullptr;
                root = root->right;
            }
        }
        else {
            std::cout << root->val << ' ';
            root = root->right;
        }
    }

    std::cout << "\n";
}

3.2 中序遍历

void InOrderMorris(node *root)
{

    while (root)
    {
        if ( root->left ) {
            node *preNode = root->left;

            while ( preNode->right != nullptr && preNode->right != root) {
                preNode = preNode->right;
            }

            if ( preNode->right == nullptr ) {
                preNode->right = root;
                root = root->left;
            }
            else {
                std::cout << root->val << " ";
                preNode ->right = nullptr;
                root = root->right;
            }
        }
        else {
            std::cout << root->val << " ";
            root = root->right;
        }
    }

    std::cout << "\n";
}

3.3 后序遍历

void addPath(node *root, std::vector<int> &seq)
{

    int count = 0;

    while (root)
    {
        ++count;
        seq.emplace_back(root->val);
        root = root->right;
    }

    std::reverse(seq.rbegin(), seq.rbegin() + count);
}
void PostOrderMorris(node *rt, std::vector<int> &seq)
{

    node *root = rt;
    while (root)
    {
        if ( root->left) {
        	// 是否存在左子树
            node *preNode = root->left;

            while (preNode->right && preNode->right != root) {
                preNode = preNode->right;
            }
            if ( preNode->right) {
            	// 第二次遍历
                preNode->right = nullptr;
                // 先断链
                addPath(root->left, seq);
                root = root->right;
            }
            else {
            	// 第一次遍历标记后继
                preNode->right = root;
                root = root->left;
            }
        }
        else {
        	// 不存在即遍历右子树
            root = root->right;
        }
    }
    addPath(rt, seq);

}

Ref

leetcode