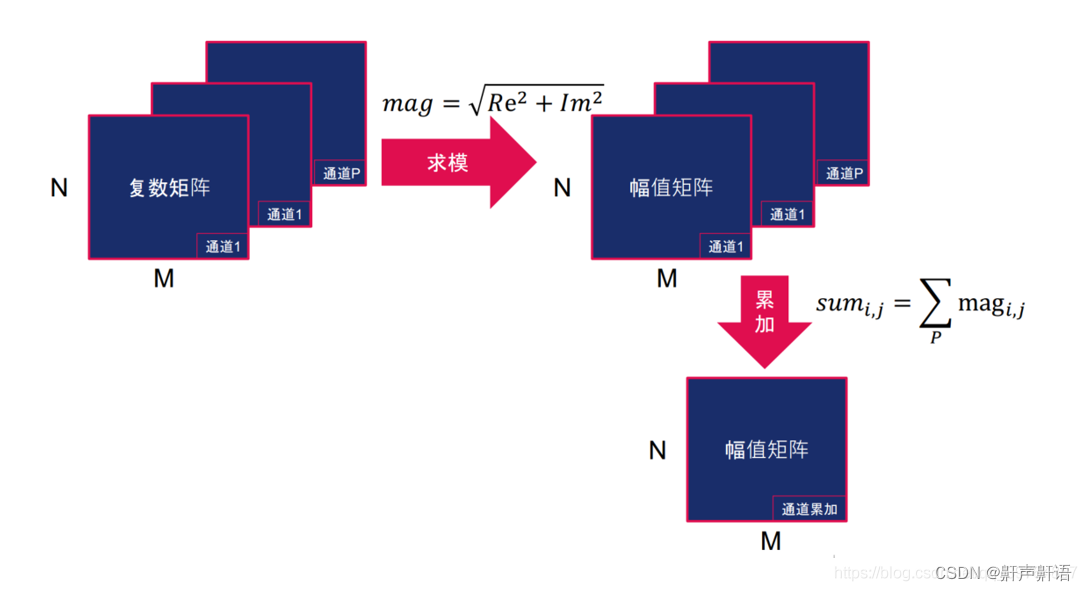
滑窗中固定只能有11帧,当来了新的帧的时候旧的帧就需要抹掉,但是不能直接把旧的帧的全部信息抹掉,因为旧的帧的经历过11次优化,其地图点中的优化信息是有用,边缘化的操作就是为了只把最旧帧的变量去掉,但是保留其对应的优化信息留在窗口里面,因为那些信息仍然具有约束作用
边缘化舒尔补
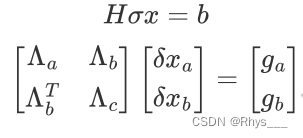
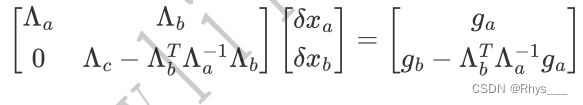

此时公式已经没有
δ
x
a
\delta x_{a}
δxa 了,但是保留了
δ
x
a
\delta x_{a}
δxa 带来的约束
δ
x
b
\delta x_{b}
δxb 左边的矩阵当作新的
H
H
H,并分解为
J
T
J
J^{T}J
JTJ,右边则分解为
J
T
e
J^{T}e
JTe
边缘化更详细的讲解看这篇文章 SLAM中的marginalization 和 Schur complement
H 矩阵的构造
由于这个
H
H
H 矩阵是在ceres中计算的,不会暴露出来,由于这里需要进行边缘化,所以只能自己计算
H
H
H 矩阵,这基本算是一个手写后端的部分了
有了
H
H
H 矩阵就可以迭代优化了,
H
Δ
x
=
g
H\Delta x=g
HΔx=g
讲一下如何构建这个 H H H 矩阵,现在存在预积分约束和重投影约束,每个约束都存在 H = J T J H=J^{T}J H=JTJ,但是现在需要一个大的 H H H 矩阵
通过把累加的方式构成这个大的矩阵
H
=
Σ
J
T
J
H=\Sigma J^{T}J
H=ΣJTJ
J
=
∂
e
∂
x
J=\frac{\partial e }{\partial x}
J=∂x∂e
状态向量有,
λ
\lambda
λ 是地图点
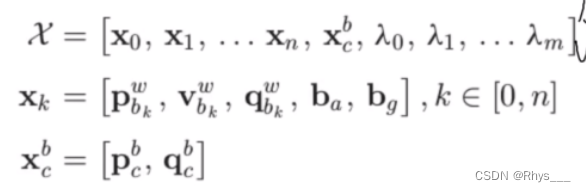
就是把每个
J
J
J都累加起来构成这个大
H
H
H
J
T
J
J^{T}J
JTJ 的形式如这张图
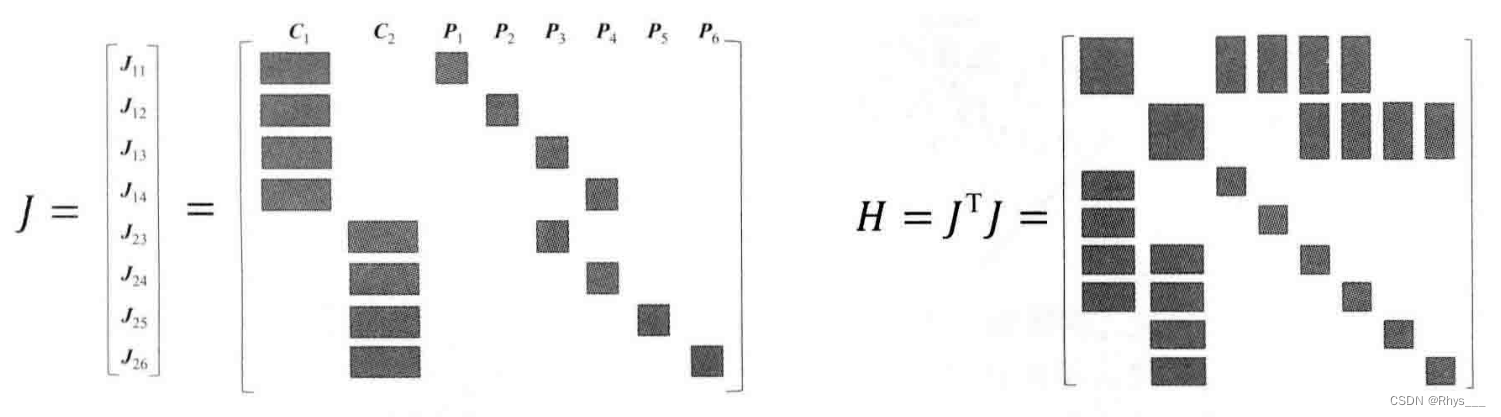
代码中要关注一下是怎么累加的
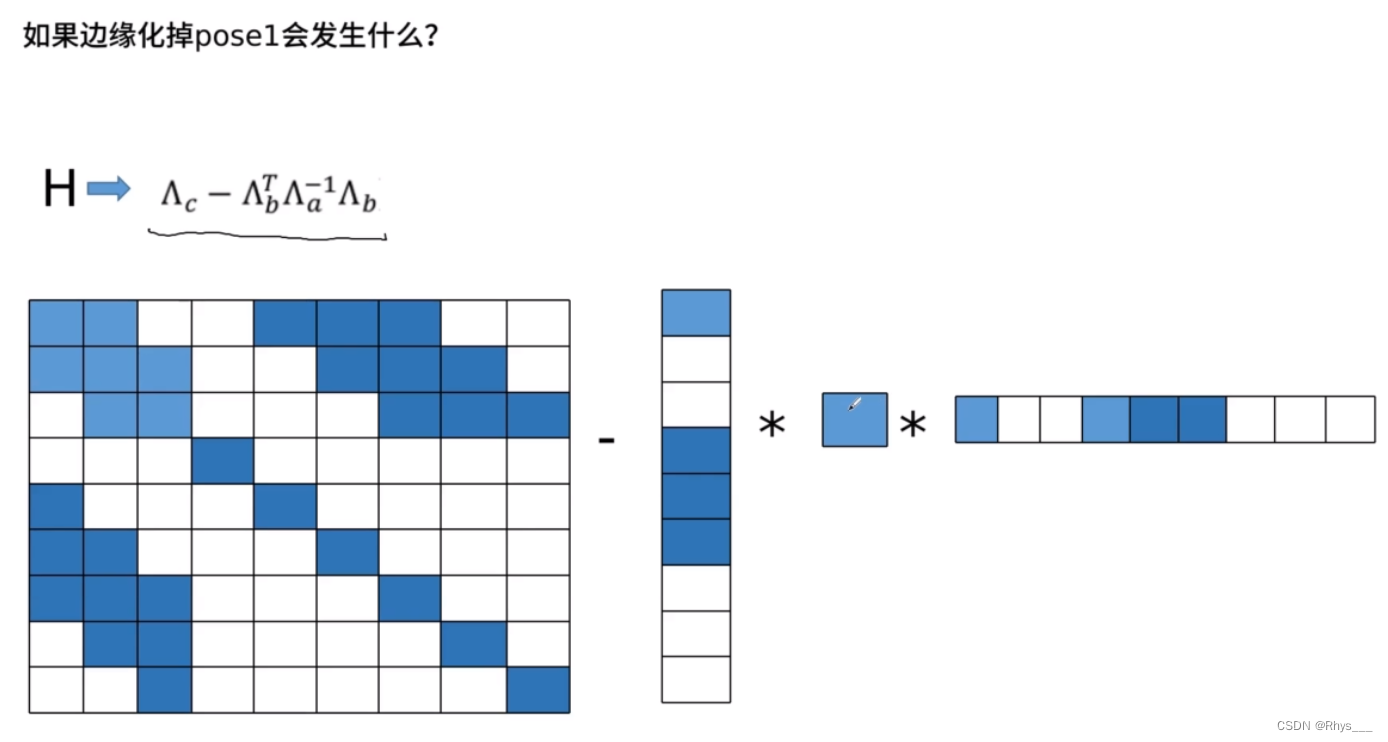
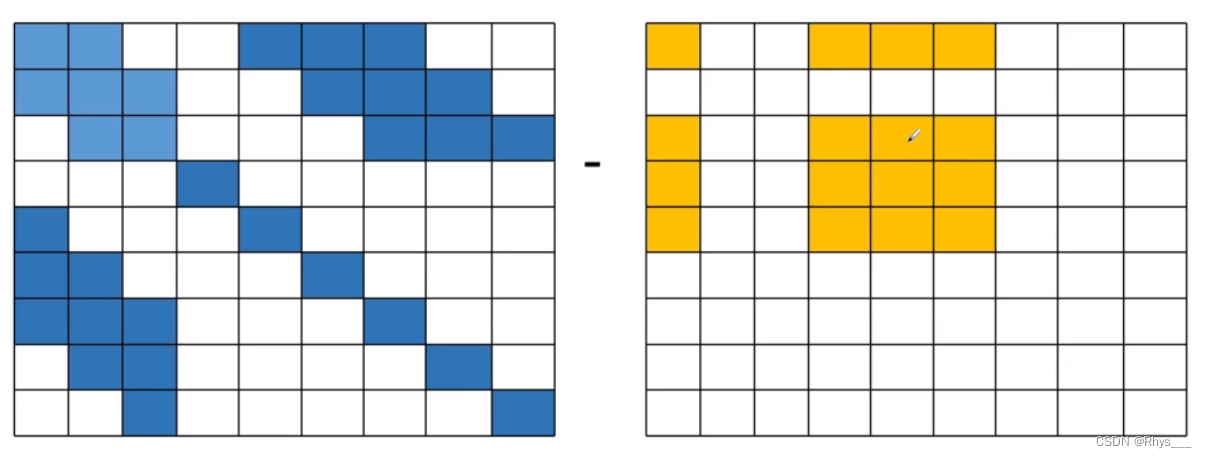
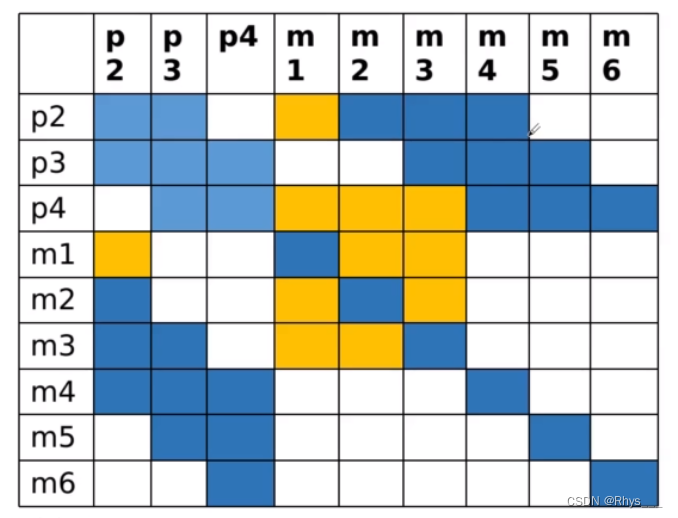
m
m
m 是地图点,
p
p
p 是位姿,可以看到
p
1
p1
p1 的量被边缘化掉了,然后对
m
1
m1
m1 和
p
2
p2
p2 建立了关系,原本
m
1
m1
m1,和
p
2
p2
p2 是没有关系的,边缘化后就建立了约束,关系图可以看下面
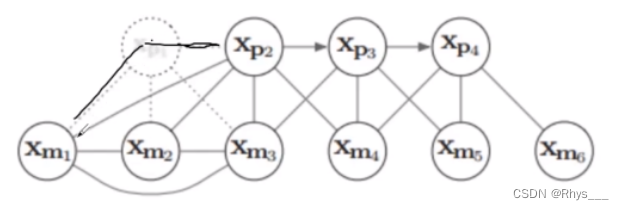
这里可以看出,边缘化会带来 fill-in 现象,把原先的稀疏矩阵变成了稠密矩阵,因为会不停地带来额外的约束
VINS中会把地图点也边缘化掉,只剩位姿,速度和零偏这些状态量的约束保留,因为地图点的数量太多了,这样可以减少矩阵的维数