[C++随笔录] AVL树

news2024/11/29 2:36:35

AVL树

  • 引言
  • AVL树的模拟实现
    • AVL树的底层结构
    • insert的实现
      • 实现思路
      • 旋转逻辑
      • insert的完整代码
    • insert的验证
  • 源码

引言

前面 二叉搜索树的时间复杂度那里提过一嘴 AVL树 和 红黑树. 因为二叉搜索树的时间复杂度是 O(高度次), 最坏情况下 -- 退化到单支链, 是 O(N); AVL 和 红黑树 可以避免这种 极端情况, 时间复杂度是 O(log N)

🗨️AVL树是如何做到避免 二叉搜索树的极端情况的呢?

  • 利用了 三叉链 && 平衡因子
    三叉链 和 平衡因子是互相成就的,.

至于它们到底是什么, 有什么妙用, 下面会有详细的解释

AVL树的模拟实现

AVL树的底层结构

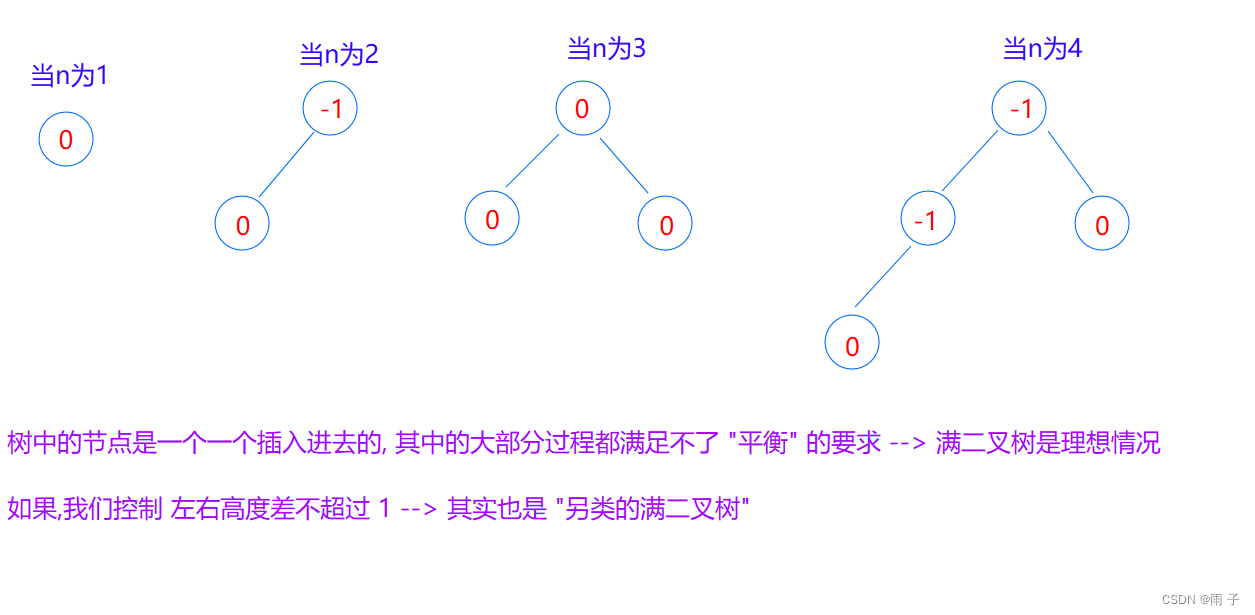
AVL树具有以下的特点:

  1. 左右子树都是AVL树
  2. 每棵子树的 高度差(平衡因子) 的绝对值不超过 1 (-1, 0 1)
  • 一般的平衡因子是 : 右子树的高度 - 左子树的高度

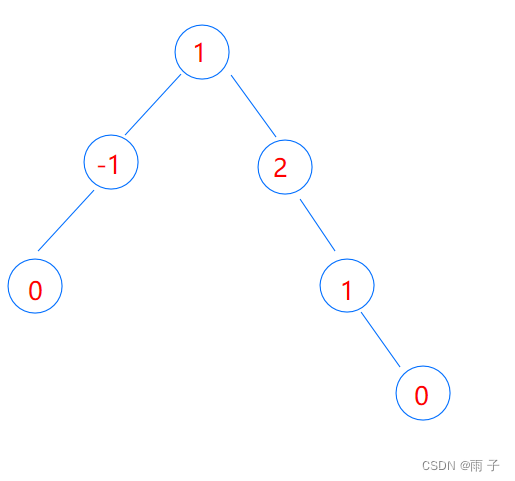
🗨️为啥不让每棵子树的 平衡因子的绝对值为 0 ?


AVL树的底层结构:

  1. AVLTreeNode类
template<class K, class V>
struct AVLTreeNode
{
public:
	AVLTreeNode(const pair<K,V>& kv)
		:_kv(kv)
	{}

public:
	pair<K, V> _kv;
	AVLTreeNode<K, V>* _left = nullptr;
	AVLTreeNode<K, V>* _right = nullptr;
	AVLTreeNode<K, V>* _parent = nullptr;
	int _bf = 0;
};
  1. AVLTree类
template<class K, class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;

public:
	AVLTree()
		:_root(nullptr)
	{}
private:
	// 根节点
	Node* _root = nullptr;
	// 记录旋转次数
	int RotateCount = 0;

};

insert的实现

实现思路

二叉树的插入逻辑 + 更新平衡因子

bool Insert(const pair<K, V>& kv)
{
	//二叉搜索树的插入逻辑
	
	if (_root == nullptr)
	{
		_root = new Node(kv);
		return true;
	}

	Node* parent = _root;
	Node* cur = _root;
	while (cur)
	{
		if (kv.first > cur->_kv.first)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (kv.first < cur->_kv.first)
		{
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			return false;
		}
	}

	// 链接
	cur = new Node(kv);
	if (cur->_kv.first > parent->_kv.first)
	{
		parent->_right = cur;
		cur->_parent = parent;
	}
	else
	{
		parent->_left = cur;
		cur->_parent = parent;
	}
	parent = cur->_parent;

	// 更新平衡因子
	// ... ...
}

那重点就是 如何更新平衡因子 :

首先, 先明确; 新插入的节点不影响自己的平衡因子, 只会影响父亲节点到 root这一段的节点的平衡因子

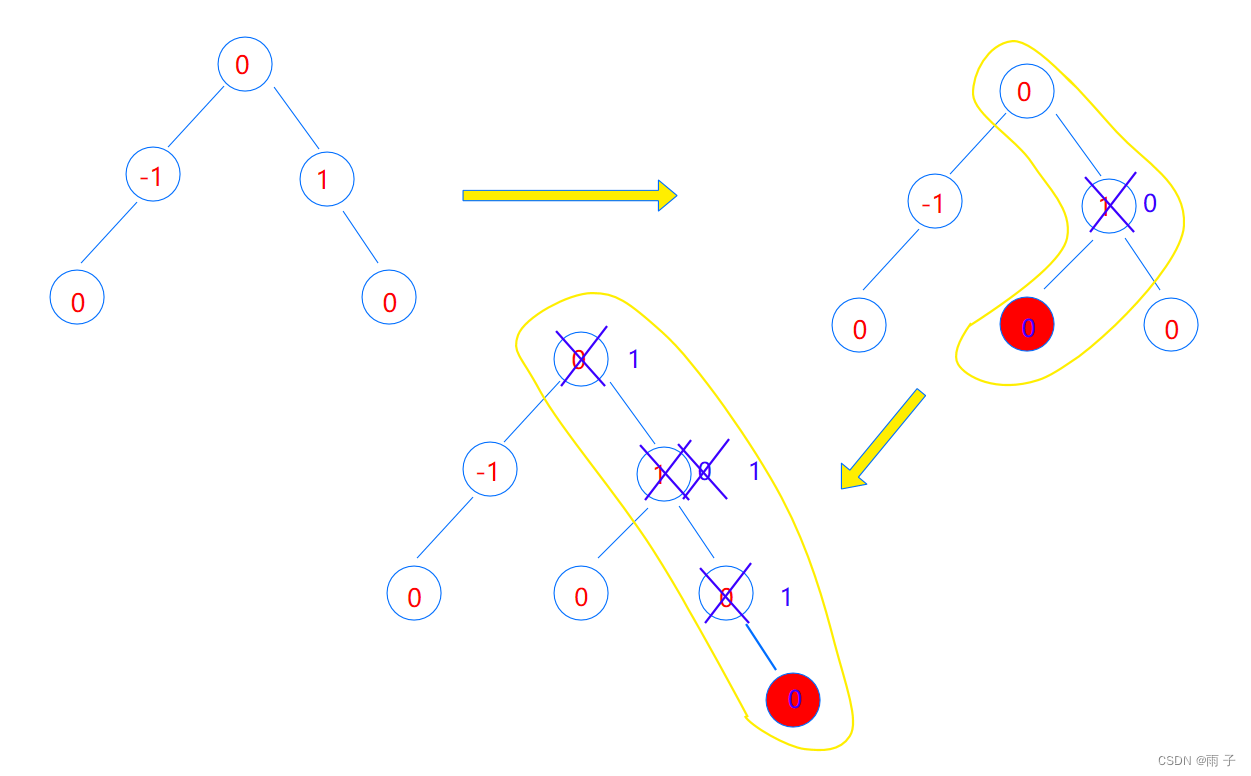
其次, 要讨论插入节点的位置

  1. 新插在左 — — parent的平衡因子减减
  2. 新插在右 — — parent的平衡因子加加

最后, 也要讨论插入后的parent的平衡因子

  1. 更新后的parent的平衡因子为 1 或 -1 — — 继续往上更新
  2. 更新后的parent的平衡因子为 0 — — 停止更新
  3. 更新后的parent的平衡因子为 2 或 -2 — — 需要旋转 — — 旋转后停止更新

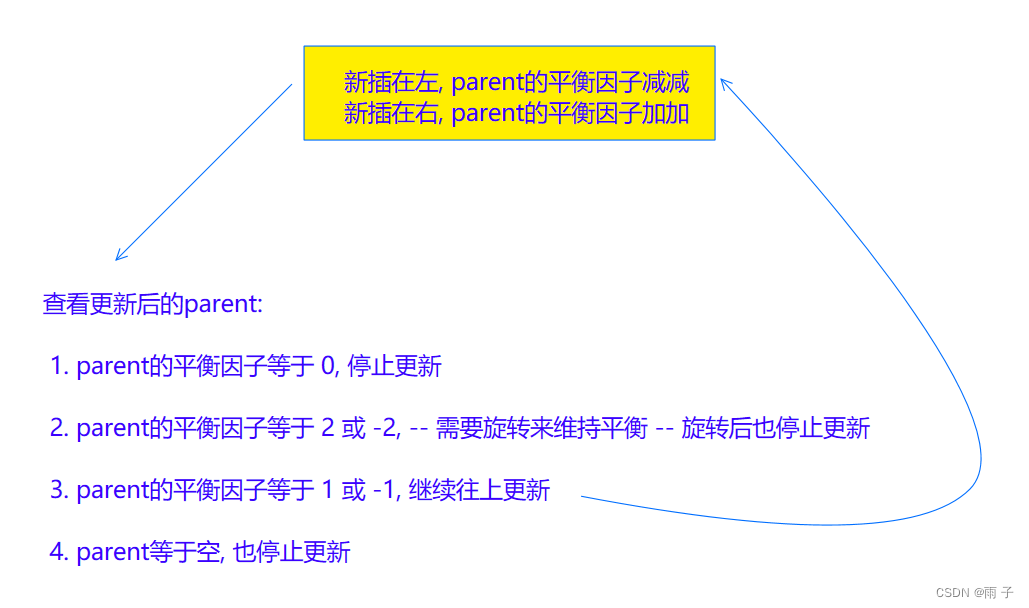
这里有几个问题:
🗨️为什么更新后的parent的平衡因子等于 1 或 -1, 要继续往上更新?

  • 更新后的parent等于 0, 说明新插入的节点并不会影响parent的高度差
    如果更新后的parent等于 1 或 -1, 说明新插入的节点影响到了parent的高度差, 有可能也会影响到parent上面的高度差 ⇒ 所以, 我们要继续向上更新, 直至 parent的平衡因子为 0 或 更新到了root

🗨️ 为什么更新后的parent等于空, 也要停止更新呢?

  • 首先, 只有root 的父亲节点才是 空
    其次,我们最差的更新情况是 更新到root节点

🗨️ 为什么旋转后就停止更新了呢?

  • 结合后面的 旋转逻辑 来进行讲解

insert的主体结构👇👇👇

bool Insert(const pair<K, V>& kv)
{
	if (_root == nullptr)
	{
		_root = new Node(kv);
		return true;
	}

	Node* parent = _root;
	Node* cur = _root;
	while (cur)
	{
		if (kv.first > cur->_kv.first)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (kv.first < cur->_kv.first)
		{
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			return false;
		}
	}

	// 链接
	cur = new Node(kv);
	if (cur->_kv.first > parent->_kv.first)
	{
		parent->_right = cur;
		cur->_parent = parent;
	}
	else
	{
		parent->_left = cur;
		cur->_parent = parent;
	}
	parent = cur->_parent;

	// 更新平衡因子
	while (parent) // 最差更新到root节点
	{
		// 1. 先更新一下parent
		// 新插在右
		if (parent->_right == cur)
		{
			parent->_bf++;
		}
		else // 新插在左
		{
			parent->_bf--;
		}

		// 2. 检查更新后的parent是否影响平衡
		if (parent->_bf == 0)
		{
			// 停止更新平衡因子
			break;
		}
		else if(parent->_bf == 1 || parent->_bf == -1)
		{
			// 继续向上更新
			cur = parent;
			parent = parent->_parent;
		}
		// 需要旋转, 来保持平衡
		else if (parent->_bf == 2 || parent->_bf == -2)
		{
			// 旋转的逻辑
			// ...
			// ...
			
			// 旋转后停止更新平衡因子
			break;
		}
	}

	return true;
}

旋转逻辑

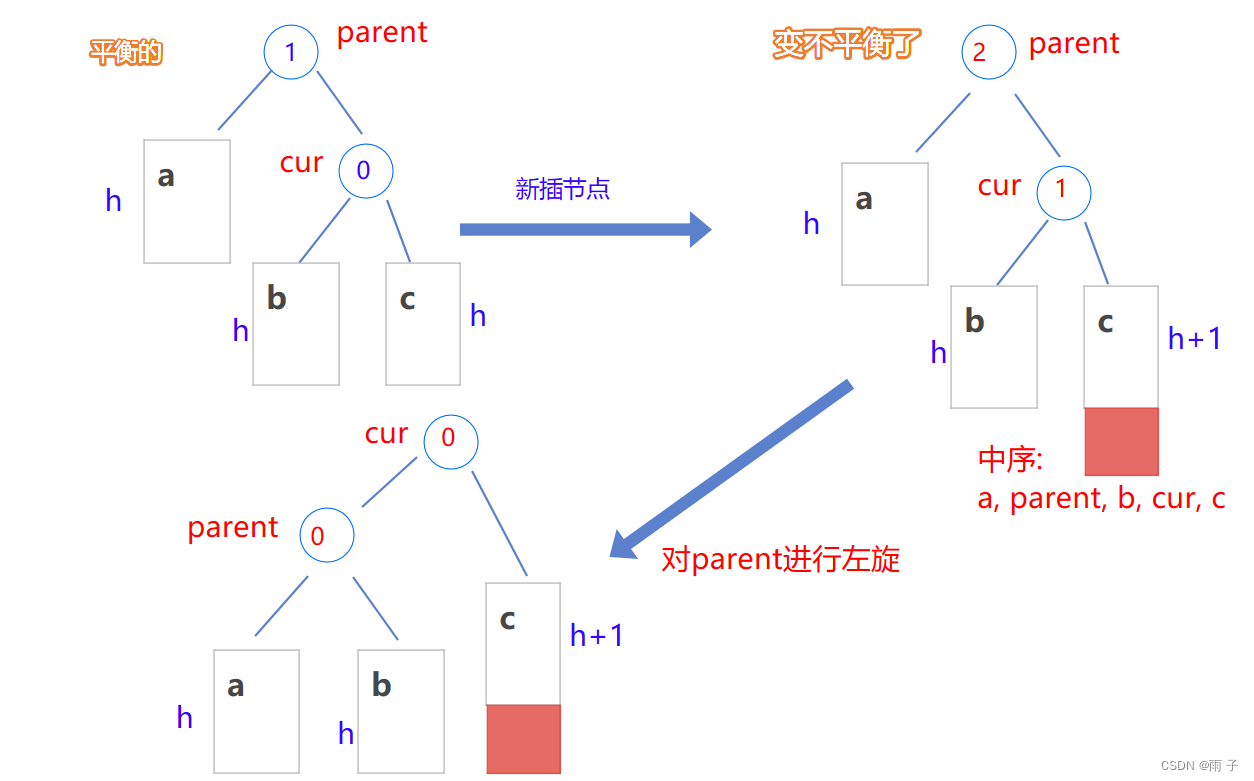
原本的树形结构符合AVL树的特点, 如果插入一个新节点 造成不平衡了, 即parent的平衡因子 等于 2 或 -2了, 这时候就要进行旋转. 根据 插入节点的位置, 一共有四种情况:

  1. 新节点插入到较高左子树的左侧 — — 左左 — — 对parent进行右旋

核心操作: 让cur的右节点充当parent的左节点, 然后让parent整体充当cur的右节点

  • 原理 :
    左边偏高 — — 想办法让左边的高度降下来 — — 把cur的左右高度差降低
    每次旋转, 也要维持 搜索树的特性 — — 中序遍历是有序的 — — cur的右节点 (b) 充当parent的左节点是合理的, parent充当 cur的右也是合理的
    ⇒ 这样以来: cur的左右子树的高度是相等的, 都为 h+1; 
void RotateL(Node* parent)
{
	// 每次旋转都++
	++RotateCount;

	// 提前保存grandfather节点, 保证后面的链接是正确的
	Node* cur = parent->_right;
	Node* grandfather = parent->_parent;
	Node* curleft = cur->_left;

	// 旋转核心
	parent->_right = curleft;
	cur->_left = parent;

	// 更新父亲
	// 1. parent && curleft
	if (curleft)
	{
		curleft->_parent = parent;
	}
	parent->_parent = cur;

	// 2.更新cur
	// cur要充当起parent的责任, 向上进行连接
	if (grandfather == nullptr)
	{
		cur->_parent = nullptr;
		_root = cur;
	}
	else
	{
		// 判读cur应该位于grandfather节点的哪一侧
		// 1. 向下进行链接
		if (grandfather->_left == parent)
		{
			grandfather->_left = cur;
		}
		else
		{
			grandfather->_right = cur;
		}
		
		// 2. 向上进行链接
		cur->_parent = grandfather;
	}

	// 更新平衡因子
	cur->_bf = parent->_bf = 0;
}
  1. 新节点插入到较高右子树的右侧 — — 右右
void RotateR(Node* parent)
{
	++RotateCount;

	Node* cur = parent->_left;
	Node* grandfather = parent->_parent;
	Node* curright = cur->_right;

	// 旋转核心
	parent->_left = curright;
	cur->_right = parent;

	// 更新链接关系
	// 1. parent && curright
	if (curright)
	{
		curright->_parent = parent;
	}
	parent->_parent = cur;

	// 2.更新cur
	if (grandfather == nullptr)
	{
		cur->_parent = nullptr;
		_root = cur;
	}
	else
	{
		if (grandfather->_left == parent)
		{
			grandfather->_left = cur;
		}
		else
		{
			grandfather->_right = cur;
		}

		cur->_parent = grandfather;
	}

	cur->_bf = parent->_bf = 0;
}
  1. 新节点插入到较高左子树的右侧 — — 左右 — — 先对cur左旋, 再对parent右旋
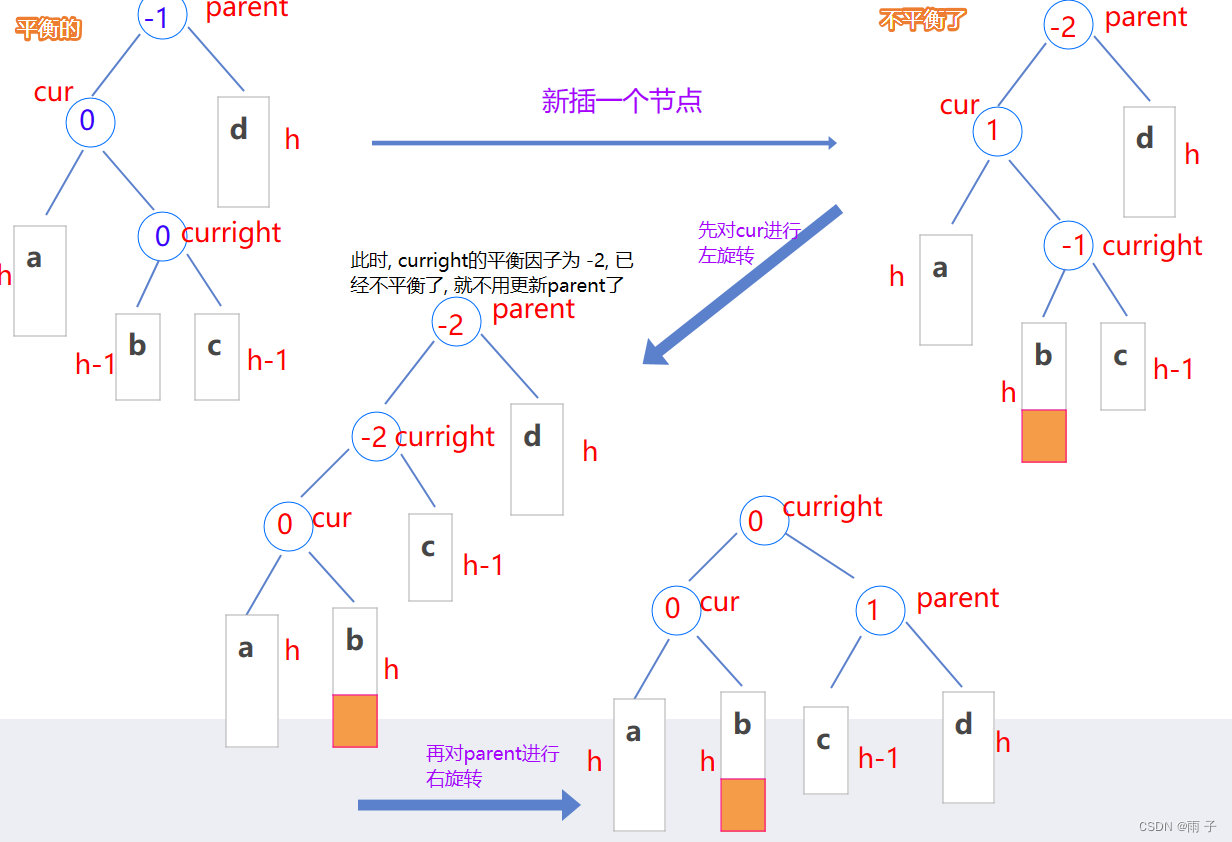
  • 其实 左右双旋的本质 是:
    把curright的左子树(b)充当cur的右子树,
    把curright的右子树(c)充当parent的左子树,
    然后curright充当根节点, cur 和 parent分别充当左右子树

⇒ 那么 更新平衡因子, 也是要看curright的左右子树(b 和 c的高度情况) :

  1. h = 0 ⇒ curright 为新增
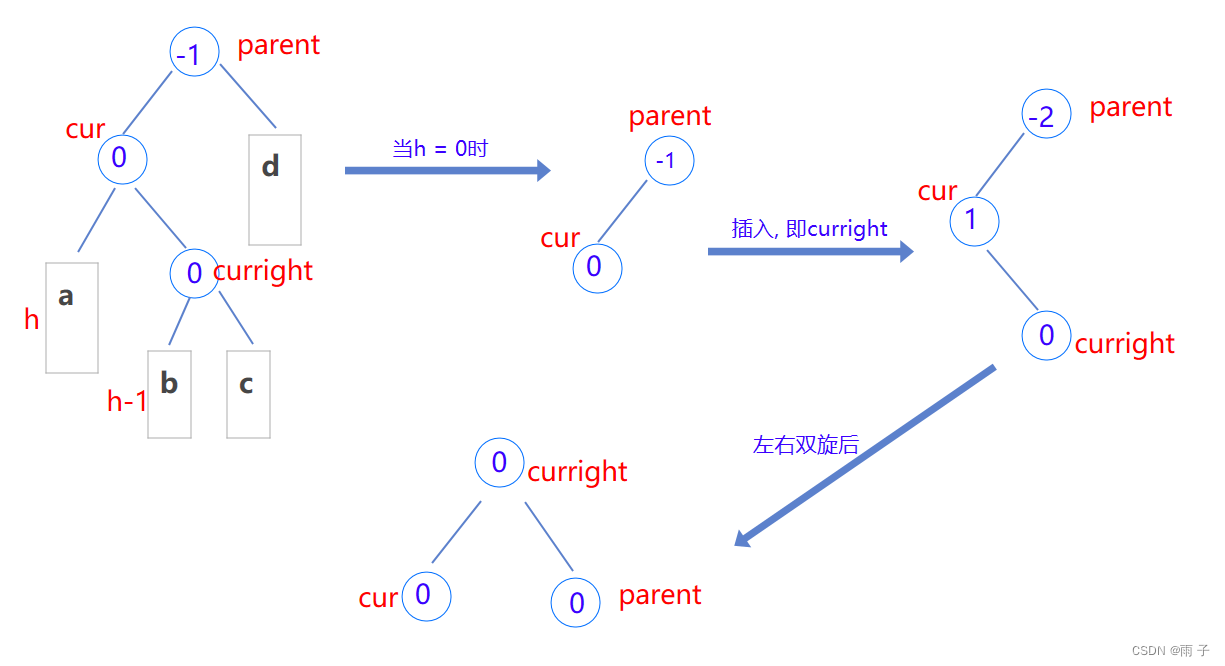
cur->bf = 0;
curright->_bf = 0;
parent->_bf = 0;
  1. h > 0 ⇒ 新增在 b 或 c
    (1)新增在 b
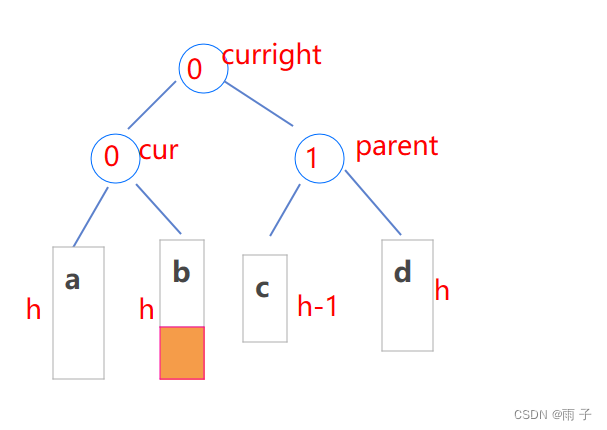
cur->bf = 0;
curright->_bf = 0;
parent->_bf = 1;

(2)新增在 c

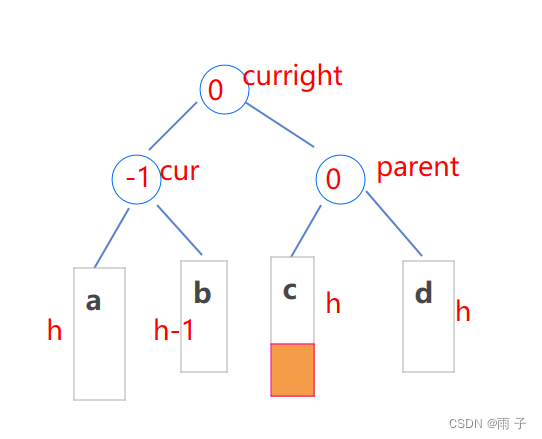
cur->bf = -1;
curright->_bf = 0;
parent->_bf = 0;

左右双旋的完整代码

void RotateLR(Node* parent)
{
	// 提前保存一份, 后面的左右旋转中会发生变化的
	Node* cur = parent->_left;
	Node* curright = cur->_right;

	RotateL(parent->_left);
	RotateR(parent);

	// 更新平衡因子
	if (curright->_bf == 0)
	{
		cur->_bf = 0;
		parent->_bf = 0;
		curright->_bf = 0;
	}
	else if (curright->_bf == 1)
	{
		cur->_bf = -1;
		parent->_bf = 0;
		curright->_bf = 0;
	}
	else if (curright->_bf == -1)
	{
		cur->_bf = 0;
		parent->_bf = 1;
		curright->_bf = 0;
	}
}
  1. 新节点插入到较高右子树的左侧 — — 右左 — — 先对cur右旋, 再对parent左旋
  • 其实, 右左双旋的本质是:
    把curleft的左子树(b) 充当 parent的右子树
    把curleft的右子树(c) 充当cur的左子树
    让curleft来根节点, 让parent 和 cur分别充当curleft的左右子树

⇒ 那么 更新平衡因子, 也是要看curleft的左右子树(b 和 c的高度情况) :

  1. h = 0 ⇒ curleft为新增
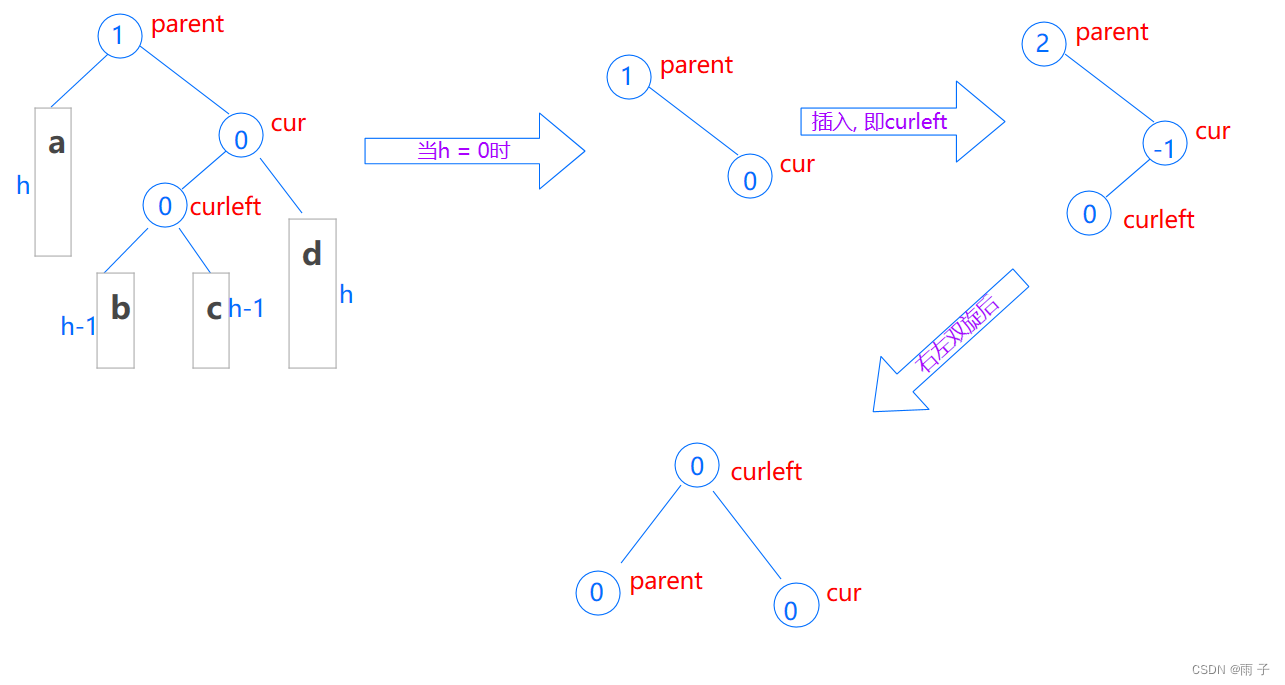
cur->bf = 0;
curleft->_bf = 0;
parent->_bf = 1;
  1. h > 0 ⇒ 新增在b / c
    (1) 新增在 b
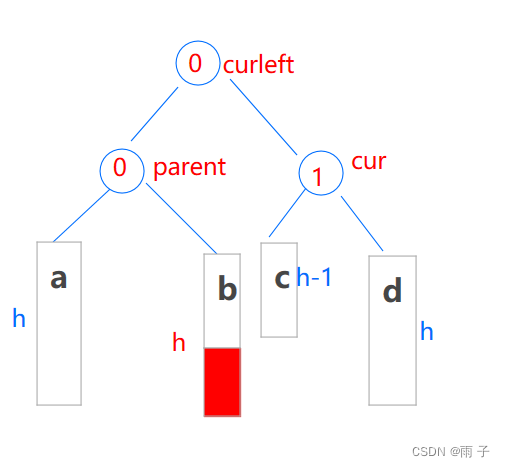
cur->bf = 1;
curleft->_bf = 0;
parent->_bf = 0;

(2) 新增在 c

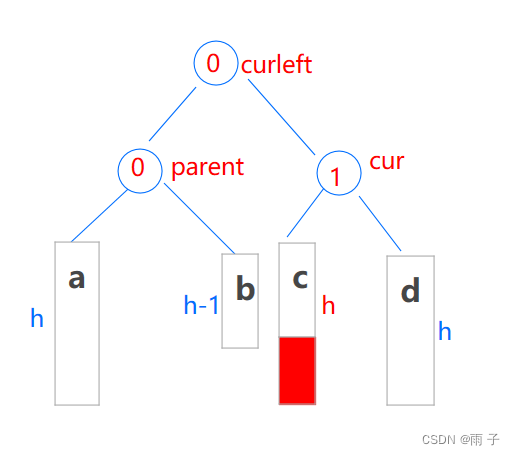
cur->bf = 0;
curleft->_bf = 0;
parent->_bf = -1;

右左双旋的完整代码

void RotateRL(Node* parent)
{
	Node* cur = parent->_right;
	Node* curleft = cur->_left;

	RotateR(parent->_right);
	RotateL(parent);

	// 更新平衡因子
	if (curleft->_bf == 0)
	{
		cur->_bf = 0;
		parent->_bf = 0;
		curleft->_bf = 0;
	}
	else if (curleft->_bf == 1)
	{
		cur->_bf = 0;
		parent->_bf = -1;
		curleft->_bf = 0;
	}
	else if (curleft->_bf == -1)
	{
		cur->_bf = 1;
		parent->_bf = 0;
		curleft->_bf = 0;
	}
}

insert的完整代码

bool Insert(const pair<K, V>& kv)
{
	if (_root == nullptr)
	{
		_root = new Node(kv);
		return true;
	}

	Node* parent = _root;
	Node* cur = _root;
	while (cur)
	{
		if (kv.first > cur->_kv.first)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (kv.first < cur->_kv.first)
		{
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			return false;
		}
	}

	// 链接
	cur = new Node(kv);
	if (cur->_kv.first > parent->_kv.first)
	{
		parent->_right = cur;
		cur->_parent = parent;
	}
	else
	{
		parent->_left = cur;
		cur->_parent = parent;
	}
	parent = cur->_parent;

	// 更新平衡因子
	while (parent)
	{
		// 1. 先更新一下parent
		// 新插在右
		if (parent->_right == cur)
		{
			parent->_bf++;
		}
		else // 新插在左
		{
			parent->_bf--;
		}

		// 2. 检查更新后的parent是否影响平衡
		if (parent->_bf == 0)
		{
			// 停止更新
			break;
		}
		else if(parent->_bf == 1 || parent->_bf == -1)
		{
			// 继续向上更新
			cur = parent;
			parent = parent->_parent;
		}
		// 需要旋转, 来保持平衡
		else if (parent->_bf == 2 || parent->_bf == -2)
		{
			if (parent->_bf == 2 && cur->_bf == 1)
			{
				RotateL(parent);
			}
			else if (parent->_bf == 2 && cur->_bf == -1)
			{
				RotateRL(parent);
			}
			else if (parent->_bf == -2 && cur->_bf == -1)
			{
				RotateR(parent);
			}
			else if (parent->_bf == -2 && cur->_bf == 1)
			{
				RotateLR(parent);
			}
			else
			{
				assert("平衡因子更新错误!");
			}
			
			// 旋转结束, 就停止更新平衡因子
			break;
		}
	}

	return true;
}

insert的验证

  1. 检查每棵子树的高度差的绝对值小于 1
  2. 检查平衡因子是否等于左右子树的高度差 ( 我们算的平衡因子有可能不对)

检查程序

int Height()
{
	return Height(_root);
}

int Height(Node* root)
{
	if (root == nullptr)
		return 0;

	int left = Height(root->_left);
	int right = Height(root->_right);

	return left > right ? left + 1 : right + 1;
}

bool Isbalance()
{
	return Isbalance(_root);
}

bool Isbalance(Node* root)
{
	if (root == nullptr)
		return true;

	int lheight = Height(root->_left);
	int rheight = Height(root->_right);
	
	if (root->_bf != rheight - lheight || abs(rheight - lheight) > 1)
	{
		cout << "平衡因子异常:" << root->_kv.first << "->" << root->_bf << endl;
		return false;
	}
	
	// 继续检查下一个支树
	return Isbalance(root->_left) && Isbalance(root->_right);
}

GetRotateCount

int GetRoateCount()
{
	return RotateCount;
}

验证代码:

void avl_test()
{
	const int N = 100000;
	vector<int> v;
	v.reserve(N);
	// srand((unsigned int)time(nullptr));

	for (size_t i = 0; i < N; i++)
	{
		// int ret = rand();
		// v.push_back(ret);

		v.push_back(i);
	}

	muyu::AVLTree<int, int> avl;
	for (auto e : v)
	{
		avl.Insert(make_pair(e, e));
	}
	
	cout << "AVL树是否达标-> " << avl.Isbalance() << endl;
	cout << "AVL树的高度-> " << avl.Height() << endl;
	cout << "AVL树旋转的次数-> " << avl.GetRoateCount() << endl;

}

int main()
{
	avl_test();
	
	return 0;
}

运行结果:

AVL树是否达标-> 1
AVL树的高度-> 17
AVL树旋转的次数-> 99983

源码

#pragma once

#include<iostream>
#include<assert.h>

using namespace std;

namespace muyu
{
	template<class K, class V>
	struct AVLTreeNode
	{
	public:
		AVLTreeNode(const pair<K,V>& kv)
			:_kv(kv)
		{}

	public:
		pair<K, V> _kv;
		AVLTreeNode<K, V>* _left = nullptr;
		AVLTreeNode<K, V>* _right = nullptr;
		AVLTreeNode<K, V>* _parent = nullptr;
		int _bf = 0;
	};

	template<class K, class V>
	class AVLTree
	{
		typedef AVLTreeNode<K, V> Node;

	public:
		AVLTree()
			:_root(nullptr)
		{}

		void RotateL(Node* parent)
		{
			// 每次旋转都++
			++RotateCount;

			// 提前保存grandfather节点, 保证后面的链接是正确的
			Node* cur = parent->_right;
			Node* grandfather = parent->_parent;
			Node* curleft = cur->_left;

			// 旋转核心
			parent->_right = curleft;
			cur->_left = parent;

			// 更新父亲
			// 1. parent && curleft
			if (curleft)
			{
				curleft->_parent = parent;
			}
			parent->_parent = cur;

			// 2.更新cur
			// cur要充当起parent的责任, 向上进行连接
			if (grandfather == nullptr)
			{
				cur->_parent = nullptr;
				_root = cur;
			}
			else
			{
				// 判读cur应该位于grandfather节点的哪一侧
				// 1. 向下进行链接
				if (grandfather->_left == parent)
				{
					grandfather->_left = cur;
				}
				else
				{
					grandfather->_right = cur;
				}
				
				// 2. 向上进行链接
				cur->_parent = grandfather;
			}

			// 更新平衡因子
			cur->_bf = parent->_bf = 0;
		}

		void RotateR(Node* parent)
		{
			++RotateCount;

			Node* cur = parent->_left;
			Node* grandfather = parent->_parent;
			Node* curright = cur->_right;

			// 旋转核心
			parent->_left = curright;
			cur->_right = parent;

			// 更新链接关系
			// 1. parent && curright
			if (curright)
			{
				curright->_parent = parent;
			}
			parent->_parent = cur;

			// 2.更新cur
			if (grandfather == nullptr)
			{
				cur->_parent = nullptr;
				_root = cur;
			}
			else
			{
				if (grandfather->_left == parent)
				{
					grandfather->_left = cur;
				}
				else
				{
					grandfather->_right = cur;
				}

				cur->_parent = grandfather;
			}

			cur->_bf = parent->_bf = 0;
		}

		void RotateRL(Node* parent)
		{
			Node* cur = parent->_right;
			Node* curleft = cur->_left;

			RotateR(parent->_right);
			RotateL(parent);

			// 更新平衡因子
			if (curleft->_bf == 0)
			{
				cur->_bf = 0;
				parent->_bf = 0;
				curleft->_bf = 0;
			}
			else if (curleft->_bf == 1)
			{
				cur->_bf = 0;
				parent->_bf = -1;
				curleft->_bf = 0;
			}
			else if (curleft->_bf == -1)
			{
				cur->_bf = 1;
				parent->_bf = 0;
				curleft->_bf = 0;
			}
		}

		void RotateLR(Node* parent)
		{
			Node* cur = parent->_left;
			Node* curright = cur->_right;

			RotateL(parent->_left);
			RotateR(parent);

			// 更新平衡因子
			if (curright->_bf == 0)
			{
				cur->_bf = 0;
				parent->_bf = 0;
				curright->_bf = 0;
			}
			else if (curright->_bf == 1)
			{
				cur->_bf = -1;
				parent->_bf = 0;
				curright->_bf = 0;
			}
			else if (curright->_bf == -1)
			{
				cur->_bf = 0;
				parent->_bf = 1;
				curright->_bf = 0;
			}
		}

		bool Insert(const pair<K, V>& kv)
		{
			if (_root == nullptr)
			{
				_root = new Node(kv);
				return true;
			}

			Node* parent = _root;
			Node* cur = _root;
			while (cur)
			{
				if (kv.first > cur->_kv.first)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (kv.first < cur->_kv.first)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return false;
				}
			}

			// 链接
			cur = new Node(kv);
			if (cur->_kv.first > parent->_kv.first)
			{
				parent->_right = cur;
				cur->_parent = parent;
			}
			else
			{
				parent->_left = cur;
				cur->_parent = parent;
			}
			parent = cur->_parent;

			// 更新平衡因子
			while (parent)
			{
				// 1. 先更新一下parent
				// 新插在右
				if (parent->_right == cur)
				{
					parent->_bf++;
				}
				else // 新插在左
				{
					parent->_bf--;
				}

				// 2. 检查更新后的parent是否影响平衡
				if (parent->_bf == 0)
				{
					break;
				}
				else if(parent->_bf == 1 || parent->_bf == -1)
				{
					// 继续向上更新
					cur = parent;
					parent = parent->_parent;
				}
				// 需要旋转, 来保持平衡
				else if (parent->_bf == 2 || parent->_bf == -2)
				{
					if (parent->_bf == 2 && cur->_bf == 1)
					{
						RotateL(parent);
					}
					else if (parent->_bf == 2 && cur->_bf == -1)
					{
						RotateRL(parent);
					}
					else if (parent->_bf == -2 && cur->_bf == -1)
					{
						RotateR(parent);
					}
					else if (parent->_bf == -2 && cur->_bf == 1)
					{
						RotateLR(parent);
					}
					else
					{
						assert("平衡因子更新错误!");
					}

					break;
				}
			}

			return true;
		}

		int Height()
		{
			return Height(_root);
		}

		int Height(Node* root)
		{
			if (root == nullptr)
				return 0;

			int left = Height(root->_left);
			int right = Height(root->_right);

			return left > right ? left + 1 : right + 1;
		}

		bool Isbalance()
		{
			return Isbalance(_root);
		}

		bool Isbalance(Node* root)
		{
			if (root == nullptr)
				return true;

			int lheight = Height(root->_left);
			int rheight = Height(root->_right);

			if (root->_bf != rheight - lheight || abs(rheight - lheight) > 1)
			{
				cout << "平衡因子异常:" << root->_kv.first << "->" << root->_bf << endl;
				return false;
			}

			return Isbalance(root->_left) && Isbalance(root->_right);
		}

		int GetRoateCount()
		{
			return RotateCount;
		}

	private:
		Node* _root = nullptr;
		int RotateCount = 0;

	};
}

富家不用买良田，书中自有千钟粟。
安居不用架高堂，书中自有黄金屋。
出门无车毋须恨，书中有马多如簇。
娶妻无媒毋须恨，书中有女颜如玉。
男儿欲遂平生志，勤向窗前读六经。
— — 赵恒《劝学诗》

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1187757.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

工业摄像机参数计算

工业摄像机参数计算

在工业相机选型的时候有点懵&#xff0c;有一些参数都不知道咋计算的。有些概念也没有区分清楚。‘’ 靶面尺寸 CMOS 或者是 CCD 使用几分之几英寸来标注的时候&#xff0c;这个几分之几英寸计算的是什么尺寸&#xff1f; 一开始我以为这个计算的就是靶面的实际对角线的尺寸…
阅读更多...
基于i.MX6ULL的掉电检测设计与软件测试

基于i.MX6ULL的掉电检测设计与软件测试

基于i.MX6ULL平台设计实现掉电检测功能&#xff0c;首先选择一路IO&#xff0c;利用IO电平变化触发中断&#xff0c;在编写驱动时捕获该路GPIO的中断&#xff0c;然后在中断响应函数中发送信号通知应用程序掉电发生了。 图 1.1 掉电信号IO 驱动代码: #include <linux/modul…
阅读更多...
AIGC视频生成/编辑技术调研报告

AIGC视频生成/编辑技术调研报告

人物AIGC&#xff1a;FaceChain人物写真生成工业级开源项目&#xff0c;欢迎上github体验。 简介&#xff1a; 随着图像生成领域的研究飞速发展&#xff0c;基于diffusion的生成式模型取得效果上的大突破。在图像生成/编辑产品大爆发的今天&#xff0c;视频生成/编辑技术也引起…
阅读更多...
【多语言多商户跨境商城系统.源码开源无加密】—— 打破语言障碍，实现全球商业连接

【多语言多商户跨境商城系统.源码开源无加密】—— 打破语言障碍，实现全球商业连接

随着全球电子商务的飞速发展&#xff0c;多语言多商户跨境商城系统已成为行业内的热门需求。这类系统能够有效地解决跨国交易中的语言沟通难题&#xff0c;同时为多商户提供公平的交易平台&#xff0c;实现全球商业连接。 今天&#xff0c;我们为您推荐一款多语言多商户跨境商城…
阅读更多...
3、FFmpeg基础

3、FFmpeg基础

1、FFmpeg 介绍 FFmpeg是一套可以用来记录、转换数字音频、视频&#xff0c;并能将其转化为流的开源计算机程序。采用LGPL或GPL许可证。它提供了录制、转换以及流化音视频的完整解决方案。它包含了非常先进的音频/视频编解码库。 2、FFmpeg 组成 - libavformat&#xff1a;用于…
阅读更多...
java项目之电子资源管理系统（ssm+jsp）

java项目之电子资源管理系统（ssm+jsp）

风定落花生&#xff0c;歌声逐流水&#xff0c;大家好我是风歌&#xff0c;混迹在java圈的辛苦码农。今天要和大家聊的是一款基于ssm的电子资源管理系统。项目源码以及部署相关请联系风歌&#xff0c;文末附上联系信息 。 项目简介&#xff1a; &#xff08;1&#xff09;在个…
阅读更多...
Redis系列-Redis性能优化与安全【9】

Redis系列-Redis性能优化与安全【9】

目录 Redis系列-Redis性能优化与安全【9】Redis性能优化策略Redis安全设置与防护措施Redis监控与诊断工具介绍 七、Redis应用案例与实战八、Redis未来发展与趋势 个人主页: 【⭐️个人主页】 需要您的【&#x1f496; 点赞关注】支持 &#x1f4af; Redis系列-Redis性能优化与安…
阅读更多...
Milvus Cloud——什么是 Agent？

Milvus Cloud——什么是 Agent？

什么是 Agent？ 根据 OpenAI 科学家 Lilian Weng 的一张 Agent 示意图 [1] 我们可以了解 Agent 由一些组件来组成。 规划模块 子目标分解：Agent 将目标分为更小的、易于管理的子目标，从而更高效地处理复杂的任务。 反省和调整：Agent 可以对过去的行为进行自我批评和自我反思…
阅读更多...
【Linux】 awk命令使用

【Linux】 awk命令使用

AWK 是一种处理文本文件的语言&#xff0c;是一个强大的文本分析工具。 之所以叫 AWK 是因为其取了三位创始人 Alfred Aho&#xff0c;Peter Weinberger, 和 Brian Kernighan 的 Family Name 的首字符。 语法 awk [选项] [文件] awk [选项] [程序] [文件] awk命令 -Linux手…
阅读更多...
磁盘空间占用巨大的meta.db-wal文件缓存（tracker-miner-fs索引服务）彻底清除办法

磁盘空间占用巨大的meta.db-wal文件缓存（tracker-miner-fs索引服务）彻底清除办法

磁盘命令参考本博客linux磁盘空间满了怎么办. 问题: 磁盘空间被盗 今天瞄了一下我的Ubuntu系统盘&#xff0c; nftdiggernftdigger-Ubuntu:~$ df -h 文件系统 容量 已用 可用 已用% 挂载点 udev 16G 0 16G 0% /dev tmpfs 3.2G 1.9…
阅读更多...
3.5米分辨率地表温度图像——商业热红外遥感卫星HotSat-1第一批数据发布

3.5米分辨率地表温度图像——商业热红外遥感卫星HotSat-1第一批数据发布

最近几年上百颗的光学和雷达商业遥感卫星发射升空&#xff0c;空间分辨率更高&#xff0c;性能更强&#xff0c;竞争也越来越激烈。除了光学和雷达遥感卫星之外&#xff0c;也出现了不少多样化传感器的商业遥感卫星&#xff0c;高光谱、热红外、无线电掩星等。不同的传感器获取…
阅读更多...
关于 DC电源模块的体积与功率达到平衡的关系

关于 DC电源模块的体积与功率达到平衡的关系

关于BOSHIDA DC电源模块的体积与功率达到平衡的关系 DC电源模块是一种将交流电转换为直流电的装置。它是许多电子设备中非常重要的部分&#xff0c;尤其是电子产品的便携性和用电时间方面&#xff0c;一直是DC电源模块必须考虑的因素。因此&#xff0c;电源模块的体积和功率之…
阅读更多...
CAN2无法通信问题

CAN2无法通信问题

文章目录 一、CAN2通信要注意的问题二、CAN中断无法进入的问题 一、CAN2通信要注意的问题 从这张图片不难看出can1为主机&#xff0c;can2为从机。因此can2的启动前提是已经启动了can1. can通讯can2是基于can1的 使用can2之前必须初始化can1 单独使用CAN2时一定要同时打开CAN1和…
阅读更多...
数据采集代码示例

数据采集代码示例

首先&#xff0c;你需要安装一个 Lua 的爬虫库&#xff0c;例如 Luanode 或者 Lush&#xff1a; lua local ltn12 require("ltn12") local http require("") local response http.request{ host "", port , path "/", …
阅读更多...
MySQL 5.7停服你的数据库还没迁移怎么破？

MySQL 5.7停服你的数据库还没迁移怎么破？

10月底&#xff0c;MySQL5.7版本正式终止生命周期状态&#xff0c;即EOL&#xff08;End of Life&#xff09;&#xff0c;也就是俗称的“停服”&#xff0c;意味着该版本的用户将不能再获得新的安全补丁、版本迭代升级、维护和支持服务&#xff0c;众多使用MySQL 5.7的各个行业…
阅读更多...
linux gdb 调试 常见调试命令介绍+总结

linux gdb 调试 常见调试命令介绍+总结

1.调试前准备 -g gcc arcg.c -g -oO -o app //必须添加-g 2.调试 gdb gdb app 3.常见调试命令 set args 1 2 3 4 5 6 //设置参数 show args //查看参数 3.1执行程序 1.start2. run gdb app set args 1 2 3 4 5 start //执行一行 c //继续执行 q…
阅读更多...
了解千兆光模块和万兆光模块的标准规范

了解千兆光模块和万兆光模块的标准规范

千兆光模块和万兆光模块作为数据中心和网络领域的关键设备&#xff0c;光模块生产需要遵循一些标准规范&#xff0c;为光模块的设计、制造和应用提供统一的规则和指导&#xff0c;确保光模块在各种设备和网络环境中能够正常工作&#xff0c;并满足用户的需求和期望&#xff0c;…
阅读更多...
双十一全光谱灯哪个牌子好？双十一必备护眼台灯推荐

双十一全光谱灯哪个牌子好？双十一必备护眼台灯推荐

护眼台灯近些年来很受欢迎&#xff0c;它采用专业的技术能够帮助调节环境光的变化。尤其是在光线变化复杂的情况下&#xff0c;能够通过智能调光来改善环境&#xff0c;可以减少许多学生党上班族的近视风险&#xff0c;成为了许多学生党打工人的必备照明工具之一。不过随着它的…
阅读更多...
移除元素(双指针)

移除元素(双指针)

27. 移除元素 - 力扣&#xff08;LeetCode&#xff09; 题目描述 给你一个数组 nums 和一个值 val&#xff0c;你需要 原地 移除所有数值等于 val 的元素&#xff0c;并返回移除后数组的新长度。 不要使用额外的数组空间&#xff0c;你必须仅使用 O(1) 额外空间并 原地 修改…
阅读更多...
如何准备软考-软件设计师(上)

如何准备软考-软件设计师(上)

前言&#xff1a; 参加了2023年下半年的软考-软件设计师的考试&#xff0c;之所以参加这个考试&#xff0c;主要出于以下几个目的&#xff1a; 1.减税。虽然只有1500的额度&#xff0c;但是考虑到税率&#xff0c;其实也不少&#xff0c;而且也没有更好的省钱途径。 2.学习。…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023