目录

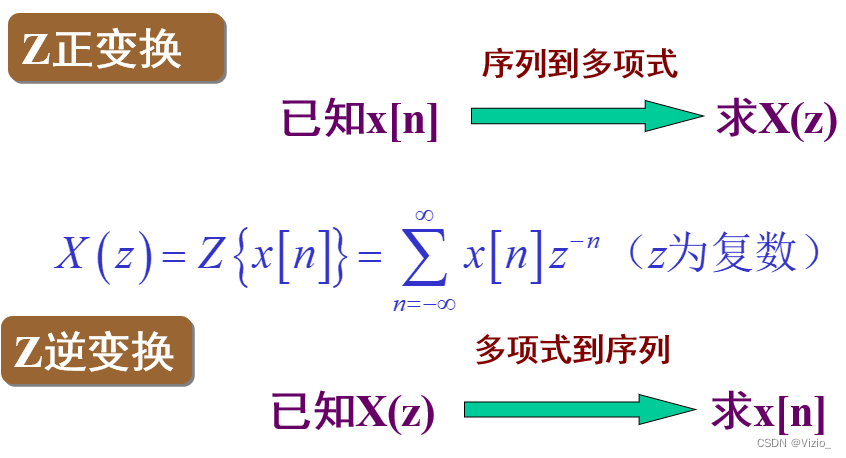
Z变换的定义:

Z变换的收敛域:

收敛域的定义:

收敛条件：

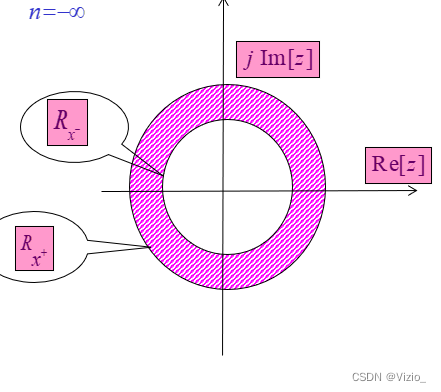
Z变换收敛域的形状：

阿贝尔定理：

对于有限长序列的收敛域：

Z变换的性质:

线性：

收敛域取交集：

时移：

指数相乘：

微分：

反序：

共轭：

X[n]初值：

卷积：

调制：

帕斯瓦尔：

逆Z变换:

留数法：

部分展开式法：

长除法：

传输函数:

从差分方程到传输函数：

传输函数和冲激响应：

频率响应的几何解释：

传输函数与稳定性：

---

Z变换的定义:

---

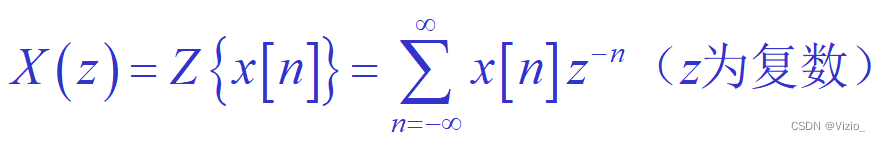
Z变换的收敛域:

收敛域的定义:

使序列x(n)的z变换x(z)收敛的所有z值的集合称作x(z)的收敛域  

收敛条件：

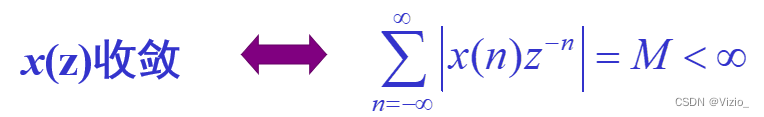
Z变换收敛域的形状：

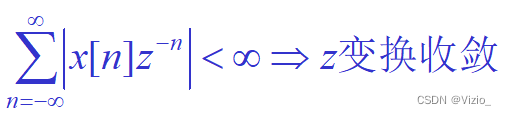
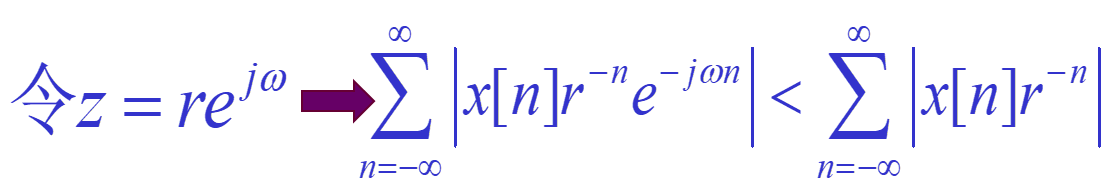
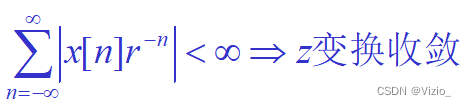
阿贝尔定理：

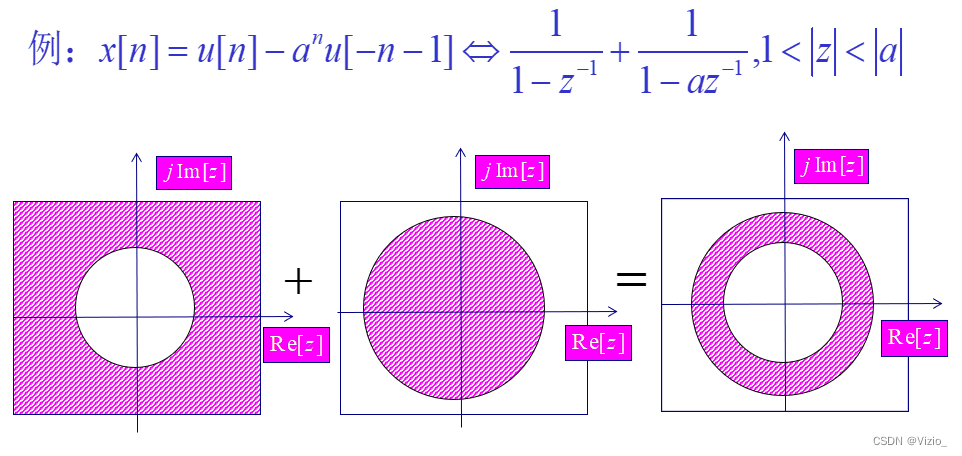
左边序列：圆周上收敛→ 圆内收敛

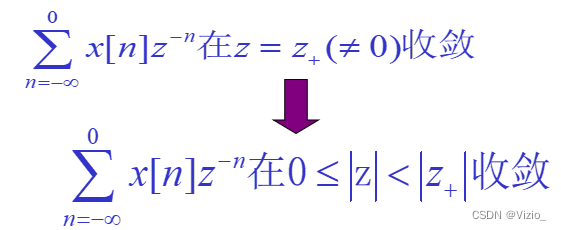
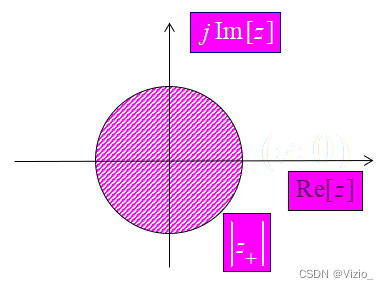
右边序列：圆周上收敛→ 圆外收敛

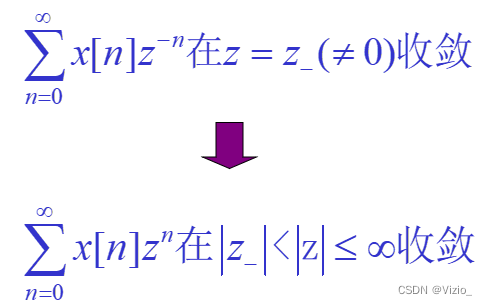
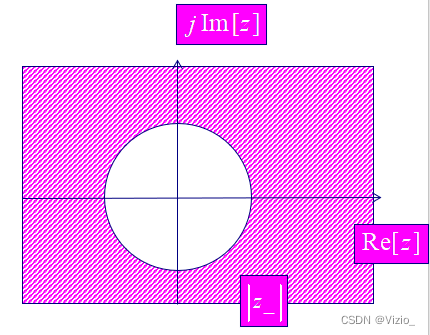
对于有限长序列的收敛域：

右边序列：

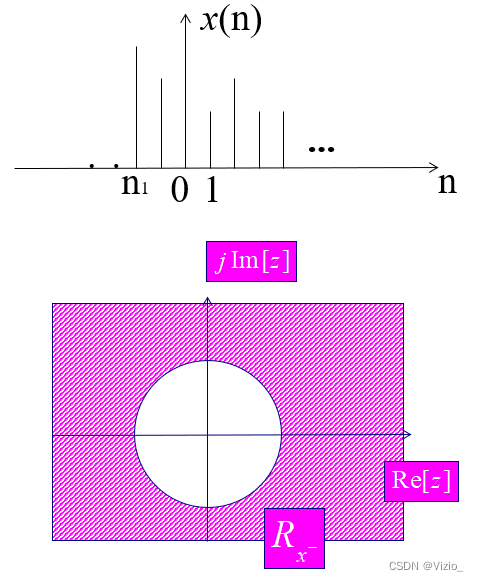
左边序列：

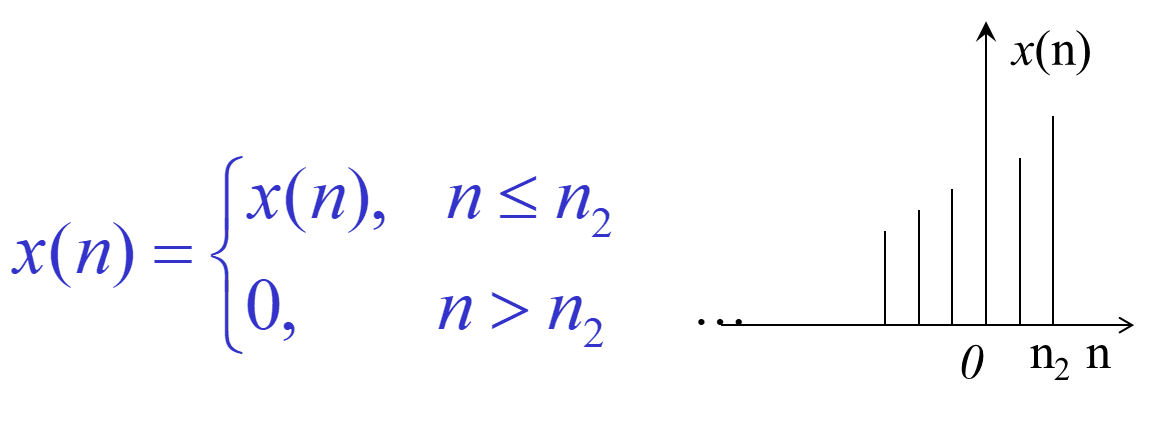
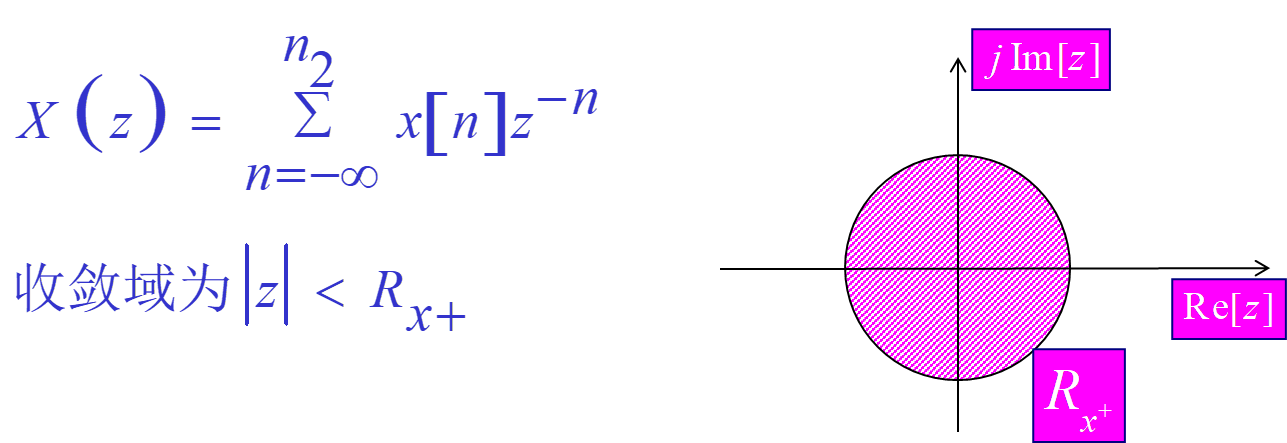
双边序列：

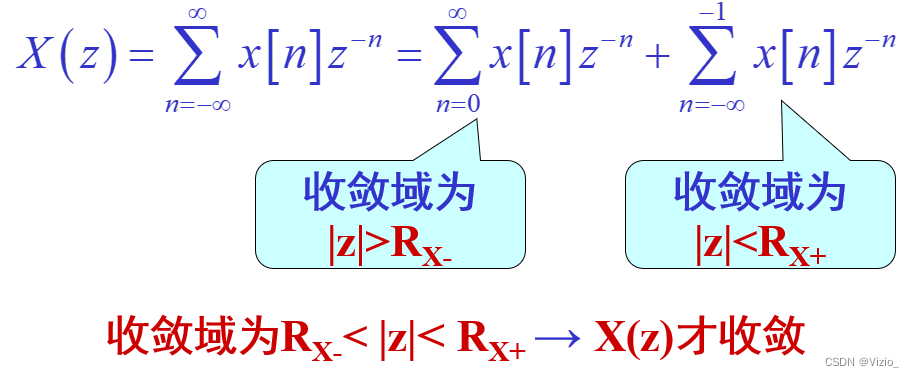
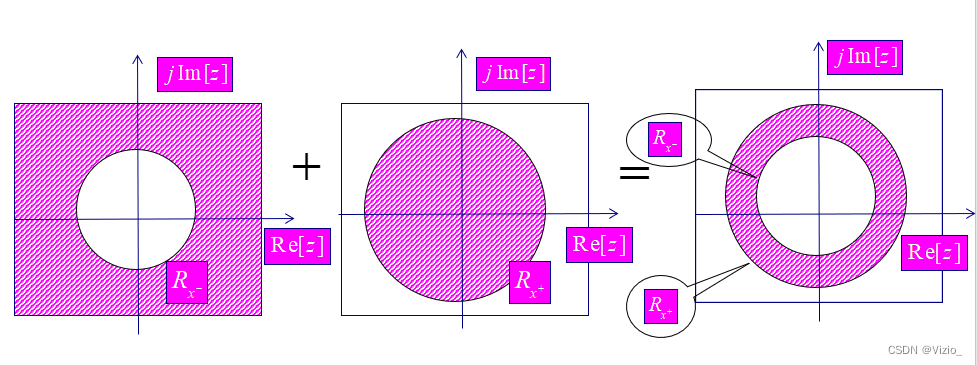
两收敛域无交集 → u[n]的Z变换不存在

---

Z变换的性质:

线性：

收敛域取交集：

时移：

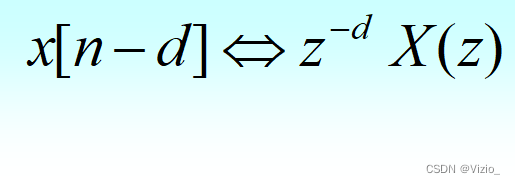
指数相乘：

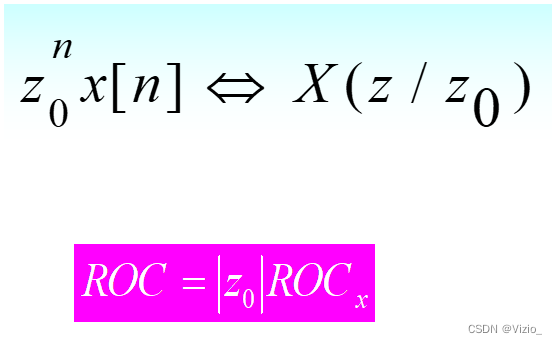
微分：

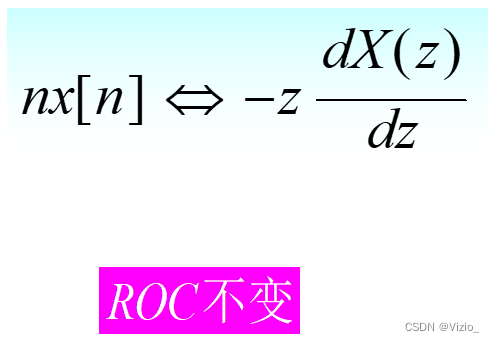
反序：

共轭：

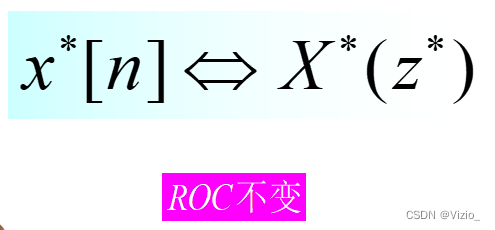
X[n]初值：

卷积：

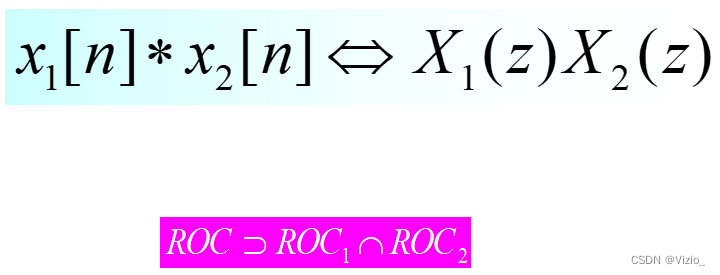
调制：

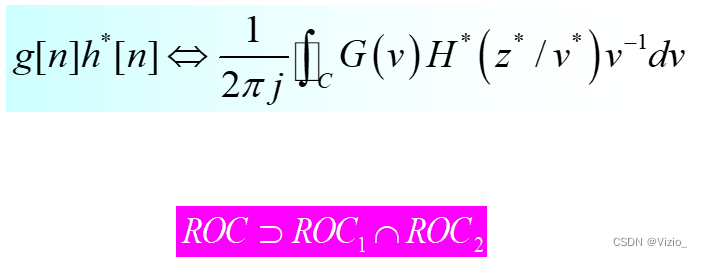
帕斯瓦尔：

---

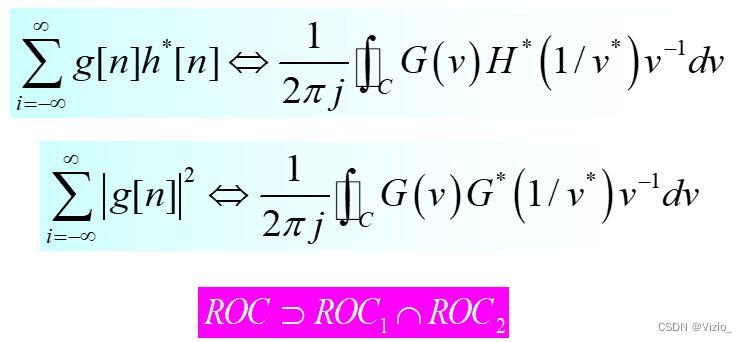
逆Z变换:

留数法：

部分展开式法：

长除法：

---

传输函数:

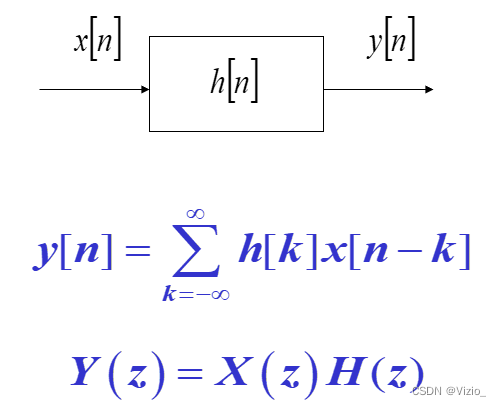
从差分方程到传输函数：

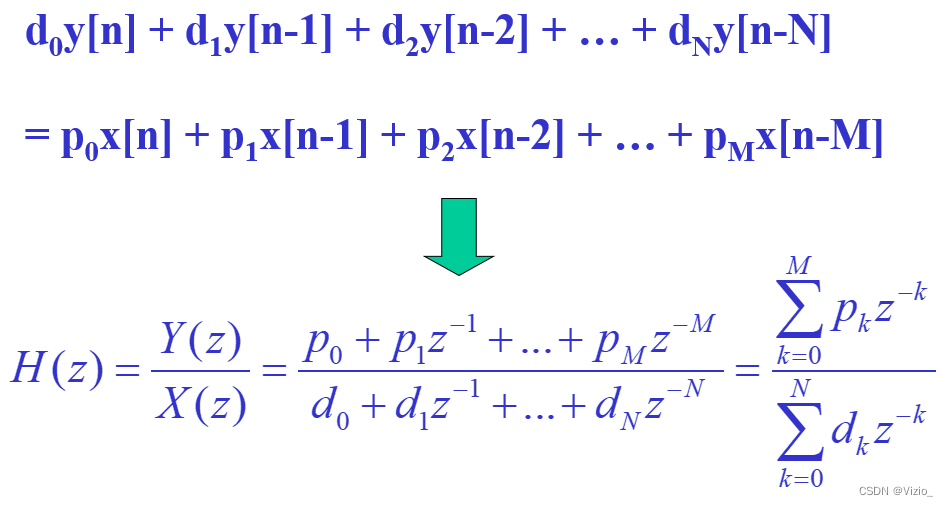
传输函数和冲激响应：

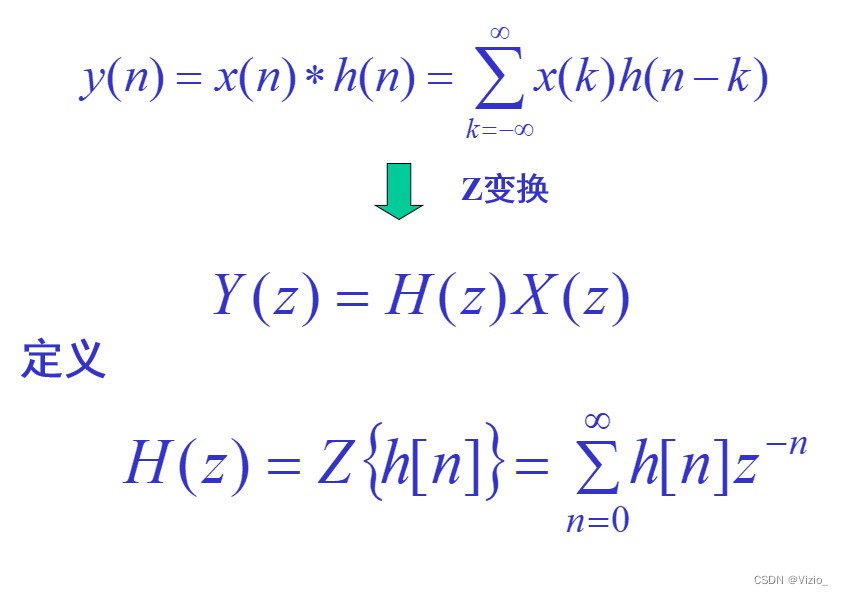
频率响应的几何解释：

传输函数与稳定性：

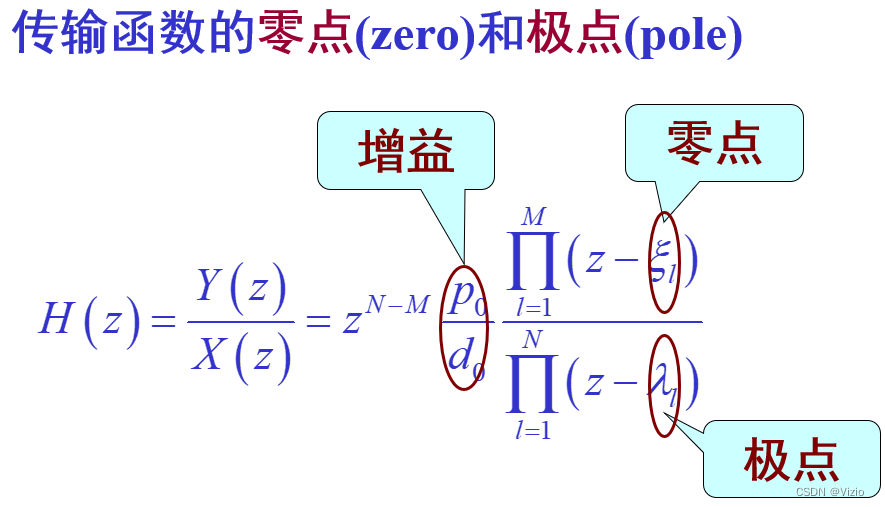
极点：对数字滤波器特性影响大

零点：调整滤波器特性，效果取决于它与极点的相对位置。

极零图(pole-zero plot )：在复z平面(z plane)上用”×”表示极点，”○”表示零点

因果稳定系统：全部极点在单位圆内

所有极点在单位圆内    →     稳定

有极点在单位圆上    →    临界

有极点在单位圆外    →    不稳定