The plus operator

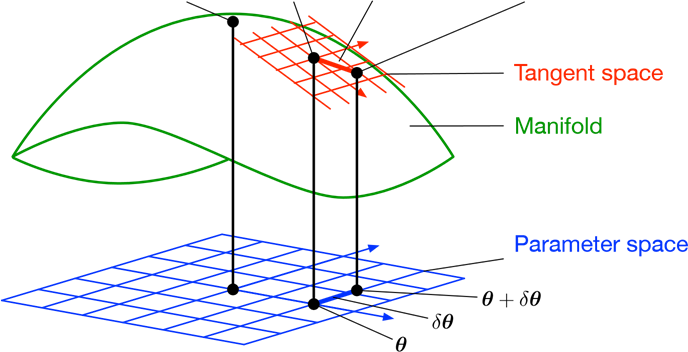
设$\mathcal{M}$表示一个n维的流型，因为流型局部同胚与${\mathbb{R}}^n$，所以我们可以通过定义符号$⊞$和$\boxminus$建立一个流型$\mathcal{M}$的局部邻域和其正切空间的双射。

$⊞:\mathcal{M}\times {\mathbb{R}}^n\to \mathcal{M};\boxminus :\mathcal{M}\times {\mathbb{M}}^n\to {\mathbb{R}}^n$

对于流型$SO(3)$，$⊞:SO(3)\times {\mathbb{R}}^n\to SO(3)$生成一个$SO(3)$中的元素，其结果是参考元素$\mathbf{R}\in SO(3)$和一个(通常很小的)旋转的组合。这个旋转由流型在参考元素$\mathbf{R}$处的正切空间中的一个向量$\theta \in {\mathbb{R}}^3$指定。
$$\mathcal{M}=SO(3):\mathbf{R}⊞\mathbf{\theta }=\mathbf{R}\mathrm{Exp}(\mathbf{\theta })$$
minus符号$\boxminus :SO(3)\times SO(3)\to {\mathbb{R}}^3$是plus符号的逆运算，它返回两个$SO(3)$元素的角度差异向量$\mathbf{\theta }\in {\mathbb{R}}^3$，角度差异向量在参考元素$\mathbf{R}$的正切空间中表示。
注意到这个符号可以定义于任意SO(3)的表示：
$$\begin{gathered} \mathbf{q}⊞\mathbf{\theta }=\mathbf{q}\otimes \mathrm{Exp}(\mathbf{\theta }) \\ \mathbf{\theta }={\mathbf{q}}_S\boxminus {\mathbf{q}}_R=\mathrm{Log}({\mathbf{q}}_R^{\ast }\otimes {\mathbf{q}}_S) \end{gathered}$$
在这两种情况下，请注意，即使向量差$\mathbf{\theta }$通常被认为是很小的，上面的定义适用于$\mathbf{\theta }$的任何值(直到SO(3)流形的第一个覆盖范围，也就是说，对于角$\theta <\pi$

四种可能的导数定义

Functions from vector space to vector space

给定一个函数$f:{\mathbb{R}}^m\to {\mathbb{R}}^n$
$$\begin{gathered} \frac{\partial f\left(\mathbf{x}\right)}{\partial \mathbf{x}}=\underset{\delta \mathbf{x}\to 0}{\lim }\frac{f\left(\mathbf{x}+\delta \mathbf{x}\right)-f\left(\mathbf{x}\right)}{\delta \mathbf{x}}\in {\mathbb{R}}^{n\times m} \\ f\left(\mathbf{x}+\Delta \mathbf{x}\right)\approx f\left(\mathbf{x}\right)+\frac{\partial f\left(\mathbf{x}\right)}{\partial \mathbf{x}}\Delta \mathbf{x}\in {\mathbb{R}}^n \end{gathered}$$

Functions from $SO(3)$ to $SO(3)$

给定函数$f:SO(3)\to SO(3)$，$\mathbf{R}\in SO(3)$和一个局部的小角度变化$\mathbf{\theta }\in {\mathbb{R}}^3$，我们使用 { ⊞ , ⊟ } \{\boxplus,\boxminus\} {⊞,⊟}定义导数：
$$\begin{array}{rl}\frac{\partial f\left(\mathbf{R}\right)}{\partial \mathbf{\theta }}& =\underset{\delta \mathbf{\theta }\to 0}{\lim }\frac{f\left(\mathbf{R}⊞\delta \mathbf{\theta }\right)\boxminus f\left(\mathbf{R}\right)}{\delta \mathbf{\theta }}\\ & =\underset{\delta \mathbf{\theta }\to 0}{\lim }\frac{\mathrm{Log}\left(f^{-1}\left(\mathbf{R}\right)f\left(\mathbf{R}\mathrm{Exp}\left(\delta \mathbf{\theta }\right)\right)\right)}{\delta \mathbf{\theta }}\in {\mathbb{R}}^{3\times 3}\\ f\left(\mathbf{R}⊞\Delta \mathbf{\theta }\right)& \approx f\left(\mathbf{R}\right)⊞\frac{\partial f\left(\mathbf{R}\right)}{\partial \mathbf{\theta }}\Delta \mathbf{\theta }\approx f\left(\mathbf{R}\right)\mathrm{Exp}\left(\frac{\partial f\left(\mathbf{R}\right)}{\partial \mathbf{\theta }}\Delta \mathbf{\theta }\right)\in SO(3)\end{array}$$

Functions from vector space to $SO(3)$

给定函数$f:{\mathbb{R}}^m\to SO(3)$，用$\boxminus$进行$SO(3)$差分，用-进行向量差分。
$$\begin{array}{rl}\frac{\partial f\left(\mathbf{x}\right)}{\partial \mathbf{x}}& =\underset{\delta \mathbf{x}\to 0}{\lim }\frac{f\left(\mathbf{x}+\delta \mathbf{x}\right)\boxminus f\left(\mathbf{x}\right)}{\delta \mathbf{x}}\\ & =\underset{\delta \mathbf{x}\to 0}{\lim }\frac{\mathrm{Log}\left(f^{-1}\left(\mathbf{x}\right)f\left(\mathbf{x}+\delta \mathbf{x}\right)\right)}{\delta \mathbf{x}}\in {\mathbb{R}}^{3\times m}\\ f\left(\mathbf{x}+\Delta \mathbf{x}\right)& \approx f\left(\mathbf{x}\right)⊞\frac{\partial f\left(\mathbf{x}\right)}{\partial \mathbf{x}}\Delta \mathbf{x}\approx f\left(\mathbf{x}\right)\mathrm{Exp}\left(\frac{\partial f\left(\mathbf{x}\right)}{\partial \mathbf{x}}\Delta \mathbf{x}\right)\in SO(3)\end{array}$$

Functions from $SO(3)$ to vector space

对于函数 $f:SO(3)\to {\mathbb{R}}^n$，用$⊞$进行$SO(3)$组合，用-进行向量差分。
$$\begin{array}{rl}\frac{\partial f\left(\mathbf{R}\right)}{\partial \mathbf{\theta }}& =\underset{\delta \mathbf{\theta }\to 0}{\lim }\frac{f\left(\mathbf{R}⊞\delta \mathbf{\theta }\right)-f\left(\mathbf{R}\right)}{\delta \mathbf{\theta }}\\ & =\underset{\delta \mathbf{\theta }\to 0}{\lim }\frac{f\left(\mathbf{R}\mathrm{Exp}\left(\delta \mathbf{\theta }\right)\right)-f\left(\mathbf{R}\right)}{\delta \mathbf{\theta }}\in {\mathbb{R}}^{n\times 3}\\ f\left(\mathbf{R}⊞\delta \mathbf{\theta }\right)& \approx f\left(\mathbf{R}\right)+\frac{\partial f\left(\mathbf{R}\right)}{\partial \mathbf{\theta }}\Delta \mathbf{\theta }\in SO(3)\end{array}$$

Jacobians of rotation

Jacobian with respect to the vector

向量旋转对于向量的求导是容易的。
$$\frac{\partial \left(\mathbf{q}\otimes \mathbf{p}\otimes {\mathbf{q}}^{\ast }\right)}{\partial \mathbf{p}}=\frac{\partial \left(\mathbf{Rp}\right)}{\partial \mathbf{p}}=\mathbf{R}$$

Jacobian with respect to the quaternion

旋转对于四元数的导数是棘手的。为了方便起见，我们使用符号$\mathbf{q}=\left[\begin{array}{cc}\mathbf{w}& \mathbf{v}\end{array}\right]=\mathbf{w}+\mathbf{v}$
$$\begin{array}{rl}{\mathbf{p}}^{\prime }& =\mathbf{q}\otimes \mathbf{p}\otimes {\mathbf{q}}^{\ast }\\ & =\left(\mathbf{w}+\mathbf{v}\right)\otimes \mathbf{p}\otimes \left(\mathbf{w}-\mathbf{v}\right)\\ & ={\mathbf{w}}^2\mathbf{p}+\mathbf{w}\left(\mathbf{v}\otimes \mathbf{p}-\mathbf{p}\otimes \mathbf{v}\right)-\mathbf{v}\otimes \mathbf{p}\otimes \mathbf{v}\\ & ={\mathbf{w}}^2\mathbf{p}+2\mathbf{w}\left(\mathbf{v}\times \mathbf{p}\right)-\left[\left(-{\mathbf{v}}^T\mathbf{p}+\mathbf{v}\times \mathbf{p}\right)\otimes \mathbf{v}\right]\\ & ={\mathbf{w}}^2\mathbf{p}+2\mathbf{w}\left(\mathbf{v}\times \mathbf{p}\right)-\left[\left(-{\mathbf{v}}^T\mathbf{p}\right)\mathbf{v}-\bcancel{{\left(\mathbf{v}\times \mathbf{p}\right)}^T\mathbf{v}}+\left(\mathbf{v}\times \mathbf{p}\right)\times \mathbf{v}\right]\\ & ={\mathbf{w}}^2\mathbf{p}+2\mathbf{w}\left(\mathbf{v}\times \mathbf{p}\right)-\left[\left(-{\mathbf{v}}^T\mathbf{p}\right)\mathbf{v}+\left({\mathbf{v}}^T\mathbf{v}\right)\mathbf{p}-\left({\mathbf{v}}^T\mathbf{p}\right)\mathbf{v}\right]\\ & ={\mathbf{w}}^2\mathbf{p}+2\mathbf{w}\left(\mathbf{v}\times \mathbf{p}\right)+2\left({\mathbf{v}}^T\mathbf{p}\right)\mathbf{v}-\left({\mathbf{v}}^T\mathbf{v}\right)\mathbf{p}\end{array}$$
进而我们能够提取出导数
$$\begin{array}{rl}\frac{\partial {\mathbf{p}}^{\prime }}{\partial \mathbf{w}}& =2\mathbf{wp}+2\mathbf{v}\times \mathbf{p}\\ \frac{\partial {\mathbf{p}}^{\prime }}{\partial \mathbf{v}}& =-2{\mathbf{wp}}^{\wedge }+2\left({\mathbf{vp}}^T+{\mathbf{v}}^T\mathbf{pI}\right)-2{\mathbf{pv}}^T\\ & =2\left({\mathbf{v}}^T\mathbf{pI}+{\mathbf{vp}}^T-{\mathbf{pv}}^T-{\mathbf{wp}}^{\wedge }\right)\end{array}$$
合并上式能够得出
$$\frac{\partial \left(\mathbf{q}\otimes \mathbf{p}\otimes {\mathbf{q}}^{\ast }\right)}{\partial \mathbf{q}}=2\left[\begin{array}{cc}\mathbf{wp}+2\mathbf{v}\times \mathbf{p}& {\mathbf{v}}^T\mathbf{pI}+{\mathbf{vp}}^T-{\mathbf{pv}}^T-{\mathbf{wp}}^{\wedge }\end{array}\right]\in {\mathbb{R}}^{3\times 4}$$

$SO(3)$的右Jacobian矩阵

$$\begin{array}{rl}& \mathrm{Exp}\left(\mathbf{\theta }\right)⊞\delta \mathbf{\varphi }=\mathrm{Exp}\left(\mathbf{\theta }+\delta \mathbf{\theta }\right)\\ ⟺& \mathrm{Exp}\left(\mathbf{\theta }\right)\cdot \mathrm{Exp}\left(\delta \mathbf{\varphi }\right)=\mathrm{Exp}\left(\mathbf{\theta }+\delta \mathbf{\theta }\right)\\ ⟺& \delta \mathbf{\varphi }=\mathrm{Log}\left(\mathrm{Exp}{\left(\mathbf{\theta }\right)}^{-1}\mathrm{Exp}\left(\mathbf{\theta }+\delta \mathbf{\theta }\right)\right)=\mathrm{Exp}\left(\mathbf{\theta }+\delta \mathbf{\theta }\right)\boxminus \mathrm{Exp}\left(\mathbf{\theta }\right)\end{array}$$
$\delta \mathbf{\varphi }$相对于$\delta \mathbf{\theta }$的微分
$$\frac{\partial \delta \mathbf{\varphi }}{\partial \delta \mathbf{\theta }}=\underset{\delta \mathbf{\theta }\to 0}{\lim }\frac{\delta \mathbf{\varphi }}{\delta \mathbf{\theta }}=\underset{\delta \mathbf{\theta }\to 0}{\lim }\frac{\mathrm{Exp}\left(\mathbf{\theta }+\delta \mathbf{\theta }\right)\boxminus \mathrm{Exp}\left(\mathbf{\theta }\right)}{\delta \mathbf{\theta }}$$
这个Jacobian矩阵就是熟知的$SO(3)$的右Jacobian矩阵，其定义为：
$$\begin{array}{rl}{\mathbf{J}}_r\left(\mathbf{\theta }\right)& =\frac{\partial \mathrm{Exp}\left(\mathbf{\theta }\right)}{\partial \mathbf{\theta }}\\ & =\underset{\delta \mathbf{\theta }\to 0}{\lim }\frac{\mathrm{Exp}\left(\mathbf{\theta }+\delta \mathbf{\theta }\right)\otimes \mathrm{Exp}\left(\mathbf{\theta }\right)}{\delta \mathbf{\theta }}\\ & =\underset{\delta \mathbf{\theta }\to 0}{\lim }\frac{\mathrm{Log}\left(\mathrm{Exp}{\left(\mathbf{\theta }\right)}^T\mathrm{Exp}\left(\mathbf{\theta }+\delta \mathbf{\theta }\right)\right)}{\delta \mathbf{\theta }}\text{if using }\mathbf{R}\\ & =\underset{\delta \mathbf{\theta }\to 0}{\lim }\frac{\mathrm{Log}\left(\mathrm{Exp}{\left(\mathbf{\theta }\right)}^{\ast }\otimes \mathrm{Exp}\left(\mathbf{\theta }+\delta \mathbf{\theta }\right)\right)}{\delta \mathbf{\theta }}\text{if using }\mathbf{q}\end{array}$$
右Jacobian矩阵及其逆矩阵的封闭形式可以计算出：
$$\begin{gathered} {\mathbf{J}}_r\left(\mathbf{\theta }\right)=I-\frac{1-\cos \Vert \mathbf{\theta }\Vert }{{\Vert \mathbf{\theta }\Vert }^2}{\mathbf{\theta }}^{\wedge }+\frac{\Vert \mathbf{\theta }\Vert -\sin \Vert \mathbf{\theta }\Vert }{{\Vert \mathbf{\theta }\Vert }^3}{\mathbf{\theta }}^{\wedge 2} \\ {\mathbf{J}}_r^{-1}\left(\mathbf{\theta }\right)=I+\frac{1}{2}{\mathbf{\theta }}^{\wedge }+\left(\frac{1}{{\Vert \mathbf{\theta }\Vert }^2}-\frac{1+\cos \Vert \mathbf{\theta }\Vert }{2\Vert \mathbf{\theta }\Vert \sin \Vert \mathbf{\theta }\Vert }\right){\mathbf{\theta }}^{\wedge 2} \end{gathered}$$
SO(3)的右Jacobian矩阵对于任意$\mathbf{\theta }$和小量$\delta \mathbf{\theta }$具有以下性质：
$$\begin{array}{rl}\mathrm{Exp}\left(\mathbf{\theta }+\delta \mathbf{\theta }\right)& \approx \mathrm{Exp}\left(\mathbf{\theta }\right)\mathrm{Exp}\left({\mathbf{J}}_r\left(\mathbf{\theta }\right)\delta \mathbf{\theta }\right)\\ \mathrm{Exp}\left(\mathbf{\theta }\right)\mathrm{Exp}\left(\delta \mathbf{\theta }\right)& \approx \mathrm{Exp}\left(\mathbf{\theta }+{\mathbf{J}}_r^{-1}\left(\mathbf{\theta }\right)\delta \mathbf{\theta }\right)\end{array}$$

Jacobian with respect to the rotation vector

∂ ( q ⊗ p ⊗ q ∗ ) ∂ δ θ = ∂ ( R p ) ∂ δ θ = − R { θ } p ∧ J r ( θ ) \dfrac{\partial \left( \bold{q}\otimes \bold{p}\otimes \bold{q}^{\ast }\right) }{\partial \delta \bm{\theta} }=\dfrac{\partial \left( \bold{R} \bold{p}\right) }{\partial \delta \bm{\theta} }=-\bold{R}\left\{ \bm{\theta} \right\} \bold{p}^{\wedge} \bold{J}_{r}\left( \bm{\theta} \right) ∂δθ∂(q⊗p⊗q∗)​=∂δθ∂(Rp)​=−R{θ}p∧Jr​(θ)

扰动

局部扰动

被扰动的朝向$\tilde{\mathbf{q}}$可表示为未经扰动的朝向$\mathbf{q}$与局部小扰动$\Delta {\mathbf{q}}_{\mathcal{L}}$的组合。由于Hamilton约定，这个局部扰动出现在复合积的右边，我们也可以给出等价的旋转矩阵形式
$$\tilde{\mathbf{q}}=\mathbf{q}\otimes \Delta {\mathbf{q}}_{\mathcal{L}}\tilde{\mathbf{R}}=\mathbf{R}\Delta {\mathbf{R}}_{\mathcal{L}}$$
局部扰动很容易通过指数映射转换为切空间中定义的等效向量形式：
$${\tilde{\mathbf{q}}}_{\mathcal{L}}={\mathbf{q}}_{\mathcal{L}}\otimes \mathrm{Exp}\left(\Delta {\mathbf{\varphi }}_{\mathcal{L}}\right){\tilde{\mathbf{R}}}_{\mathcal{L}}={\mathbf{R}}_{\mathcal{L}}\mathrm{Exp}\left(\Delta {\mathbf{\varphi }}_{\mathcal{L}}\right)$$
局部扰动的表示为：
$$\Delta {\mathbf{\varphi }}_{\mathcal{L}}=\mathrm{Log}\left({\mathbf{q}}_{\mathcal{L}}^{\ast }\otimes {\tilde{\mathbf{q}}}_{\mathcal{L}}\right)=\mathrm{Log}\left({\mathbf{R}}_{\mathcal{L}}^T\cdot {\tilde{\mathbf{R}}}_{\mathcal{L}}\right)$$
如果扰动角$\Delta {\mathbf{\varphi }}_{\mathcal{L}}$足够小，则四元数形式的扰动和旋转矩阵形式的扰动可以近似为泰勒展开直到线性项
$$\begin{array}{rl}\Delta {\mathbf{q}}_{\mathcal{L}}& =\mathrm{Exp}\left(\Delta {\mathbf{\varphi }}_{\mathcal{L}}\right)\approx 1+\frac{1}{2}\Delta {\mathbf{\varphi }}_{\mathcal{L}}=\left[\begin{array}{c}1\\ \frac{1}{2}\Delta {\mathbf{\varphi }}_{\mathcal{L}}\end{array}\right]\\ \Delta {\mathbf{R}}_{\mathcal{L}}& =\mathrm{Exp}\left(\Delta {\mathbf{\varphi }}_{\mathcal{L}}\right)=I+\Delta {\mathbf{\varphi }}_{\mathcal{L}}^{\wedge }\end{array}$$
因此，扰动可以在与$SO(3)$流形相切的局部向量空间中指定。在这个向量空间中表示这些扰动的协方差矩阵是很方便的，即用一个3×3协方差矩阵表示。

全局扰动

全局扰动出现在复合积的左侧
$${\tilde{\mathbf{q}}}_{\mathcal{G}}=\mathrm{Exp}\left(\Delta {\mathbf{\varphi }}_{\mathcal{G}}\right)\otimes {\mathbf{q}}_{\mathcal{G}}{\tilde{\mathbf{R}}}_{\mathcal{G}}=\mathrm{Exp}\left(\Delta {\mathbf{\varphi }}_{\mathcal{G}}\right)\cdot {\mathbf{R}}_{\mathcal{G}}$$
全局扰动的表示为：
$$\Delta {\mathbf{\varphi }}_{\mathcal{G}}=\mathrm{Log}\left({\tilde{\mathbf{q}}}_{\mathcal{G}}\otimes {\mathbf{q}}_{\mathcal{G}}^{\ast }\right)=\mathrm{Log}\left({\tilde{\mathbf{R}}}_{\mathcal{G}}\cdot {\mathbf{R}}_{\mathcal{G}}^T\right)$$
全局扰动可以在与SO(3)流形原点处相切的向量空间中指定。

时间微分

在向量空间中表示局部扰动，我们可以很容易地得到时间导数的表达式。只要考虑$\mathbf{q}=\mathbf{q}(t)$为原始状态，$\tilde{\mathbf{q}}=\mathbf{q}(t+\Delta t)$为扰动状态，并应用导数的定义
$$\begin{array}{rl}\dot{\mathbf{q}}& =\underset{\Delta t\to 0}{\lim }\frac{\mathbf{q}\left(t+\Delta t\right)-\mathbf{q}\left(t\right)}{\Delta t}\\ & =\underset{\Delta t\to 0}{\lim }\frac{\mathbf{q}\otimes \Delta {\mathbf{q}}_{\mathcal{L}}-\mathbf{q}}{\Delta t}\\ & =\underset{\Delta t\to 0}{\lim }\frac{\mathbf{q}\otimes \left(\left[\begin{array}{c}1\\ \Delta {\mathbf{\varphi }}_{\mathcal{L}}/2\end{array}\right]-\left[\begin{array}{c}1\\ 0\end{array}\right]\right)}{\Delta t}\\ & =\underset{\Delta t\to 0}{\lim }\frac{\mathbf{q}\otimes \left[\begin{array}{c}0\\ \Delta {\mathbf{\varphi }}_{\mathcal{L}}/2\end{array}\right]}{\Delta t}\\ & =\frac{1}{2}\mathbf{q}\otimes \left[\begin{array}{c}0\\ {\mathbf{\omega }}_{\mathcal{L}}\end{array}\right]\end{array}$$
其中$\Delta {\mathbf{\varphi }}_{\mathcal{L}}$为局部扰动角,对应于由$\mathbf{q}$定义的局部坐标系,${\mathbf{\omega }}_{\mathcal{L}}$是对应的角度变化率
$${\mathbf{\omega }}_L\left(t\right)=\frac{d{\mathbf{\varphi }}_{\mathcal{L}}\left(t\right)}{dt}=\underset{\Delta t\to 0}{\lim }\frac{\Delta {\mathbf{\varphi }}_{\mathcal{L}}}{\Delta t}$$
定义
$$\mathbf{\Omega }(\mathbf{\omega })\triangleq {\left[\mathbf{\omega }\right]}_R=\left[\begin{array}{cc}0& -{\mathbf{\omega }}^T\\ \mathbf{\omega }& -{\mathbf{\omega }}^{\wedge }\end{array}\right]$$
可以得到
$$\dot{\mathbf{q}}=\frac{1}{2}\mathbf{\Omega }({\mathbf{\omega }}_{\mathcal{L}})\mathbf{q}=\frac{1}{2}\mathbf{q}\otimes {\mathbf{\omega }}_{\mathcal{L}},\dot{\mathbf{R}}=\mathbf{R}{\mathbf{\omega }}_{\mathcal{L}}^{\wedge }\text{\hspace{1em}(1)}$$
这些表达式也可以在旋转群$SO(3)$的框架中得出的.然而在微分框架下,我们能够清楚地将角速度${\mathbf{\omega }}_{\mathcal{L}}$与一个特定的参考系联系起来.在上面这种情况下这个参考系是由方向$\mathbf{q}$或$\mathbf{R}$定义的局部坐标系.

与全局扰动相关的时间导数同理可得,其结果为
$$\dot{\mathbf{q}}=\frac{1}{2}{\mathbf{\omega }}_{\mathcal{G}}\otimes \mathbf{q},\dot{\mathbf{R}}={\mathbf{\omega }}_{\mathcal{G}}^{\wedge }\mathbf{R}\text{\hspace{1em}(2)}$$
其中
$${\mathbf{\omega }}_{\mathcal{G}}(t)\triangleq \frac{\mathrm{d}{\mathbf{\varphi }}_{\mathcal{G}}}{\mathrm{d}t}$$
是在全局坐标系中表示的角速度向量.

全局与局部的关系

$$\begin{gathered} \frac{1}{2}{\mathbf{\omega }}_{\mathcal{G}}\otimes \mathbf{q}=\dot{\mathbf{q}}=\frac{1}{2}\mathbf{q}\otimes {\mathbf{\omega }}_{\mathcal{L}} \\ ⟹{\mathbf{\omega }}_{\mathcal{G}}=\mathbf{q}\otimes {\mathbf{\omega }}_{\mathcal{L}}\otimes {\mathbf{q}}^{\ast }=\mathbf{R}{\mathbf{\omega }}_{\mathcal{L}} \end{gathered}$$
类似的,考虑$\Delta \mathbf{\varphi }\approx \mathbf{\omega }\Delta t$
$$\Delta {\mathbf{\varphi }}_{\mathcal{G}}=\mathbf{q}\otimes \Delta {\mathbf{\varphi }}_{\mathcal{L}}\otimes {\mathbf{q}}^{\ast }=\mathbf{R}\Delta {\mathbf{\varphi }}_{\mathcal{L}}$$
也就是说，我们可以使用四元数或旋转矩阵将角速率向量$\mathbf{\omega }$和小角扰动$\Delta \mathbf{\varphi }$进行坐标系变换，就像它们是普通向量一样。
由$\mathbf{\omega }=\mathbf{u}\mathbf{\omega }$，或$\Delta \mathbf{\varphi }=\mathbf{u}\Delta \mathbf{\varphi }$且旋转不改变向量长度,可以得到
$${\mathbf{u}}_{\mathcal{G}}=\mathbf{q}\otimes {\mathbf{u}}_{\mathcal{L}}\otimes {\mathbf{q}}^{\ast }=\mathbf{R}{\mathbf{u}}_{\mathcal{L}}$$

旋转速度的时间积分

对局部旋转速度定义的微分方程为(1)，对全局旋转速率定义的微分方程为(2)。通过对旋转速度的微分方程积分来完成以四元数形式积分旋转随时间的变化。在通常的情况下，角速度由局部传感器测量，从而在离散时间$t_n=n\Delta t$时提供局部测量$\mathbf{\omega }(t_n)$。因为我们主要关注微分方程(1)。
$$\dot{\mathbf{q}}(t)=\frac{1}{2}\mathbf{q}(t)\otimes \mathbf{\omega }(t)$$
定义${\mathbf{q}}_n\triangleq \mathbf{q}(t_n),{\mathbf{\omega }}_n\triangleq \mathbf{\omega }(t_n)$，由泰勒展开可得：
$${\mathbf{q}}_{n+1}={\mathbf{q}}_n+{\dot{\mathbf{q}}}_n\Delta t+\frac{1}{2!}{\ddot{\mathbf{q}}}_n\Delta t^2+\frac{1}{3!}{\mathbf{q}}_n^{(3)}\Delta t^3+\cdots$$
反复运用四元数导数的表达式，假设$\ddot{\mathbf{\omega }}=0$，可以很容易的得到${\mathbf{q}}_n$的逐次导数
$$\begin{array}{rl}{\dot{\mathbf{q}}}_n& =\frac{1}{2}{\mathbf{q}}_n{\mathbf{\omega }}_n\\ {\ddot{\mathbf{q}}}_n& =\frac{1}{2^2}{\mathbf{q}}_n{\mathbf{\omega }}_n^2+\frac{1}{2}{\mathbf{q}}_n\dot{\mathbf{\omega }}\\ {\ddot{\mathbf{q}}}_n& =\frac{1}{2^3}{\mathbf{q}}_n{\mathbf{\omega }}_n^3+\frac{1}{2^2}{\mathbf{q}}_n\dot{\mathbf{\omega }}{\mathbf{\omega }}_n+\frac{1}{2}{\mathbf{q}}_n{\mathbf{\omega }}_n\dot{\mathbf{\omega }}\\ {\mathbf{q}}_n^{(i⩾4)}& =\frac{1}{2^i}{\mathbf{q}}_n{\mathbf{\omega }}_n^i+\cdots \end{array}$$

零阶积分

前向积分
如果在$[t_n,t_{n+1}]$期间是匀角速度运动，即$\dot{\mathbf{\omega }=0}$，则有
$${\mathbf{q}}_{n+1}={\mathbf{q}}_n\otimes \left(1+\frac{1}{2}{\mathbf{\omega }}_n\Delta t+\frac{1}{2!}{\left(\frac{1}{2}{\mathbf{\omega }}_n\Delta t\right)}^2+\frac{1}{3!}{\left(\frac{1}{2}{\mathbf{\omega }}_n\Delta t\right)}^3+\cdots \right)$$
这里我们很容易就可以识别出其中的泰勒展开级数就是$e^{{\mathbf{\omega }}_n\Delta t/2}$，这个指数对应于增量旋转为$\mathbf{\theta }=\mathbf{\omega }\Delta t$
e ω Δ t / 2 = ω Δ t = q { ω Δ t } = [ cos ⁡ ( ∥ ω ∥ Δ t / 2 ) ω ∥ ω ∥ sin ⁡ ( ∥ ω ∥ Δ t / 2 ) ] e^{\bm{\omega} \Delta t/2}={\rm \bm{\omega}\Delta t}=\bold{q}\{\bm{\omega} \Delta t\}= \begin{bmatrix} \cos(\Vert\bm{\omega}\Vert\Delta t/2)\\ \frac{\bm{\omega}}{\Vert\bm{\omega}\Vert}\sin(\Vert\bm{\omega}\Vert\Delta t/2) \end{bmatrix} eωΔt/2=ωΔt=q{ωΔt}=[cos(∥ω∥Δt/2)∥ω∥ω​sin(∥ω∥Δt/2)​]
因此，
q n + 1 = q n ⊗ q { ω n Δ t } \bold{q}_{n+1}=\bold{q}_n\otimes \bold{q}\{\bm{\omega}_n \Delta t\} qn+1​=qn​⊗q{ωn​Δt}
反向积分
我们也可以认为周期$\Delta t$上的恒定角速度为${\mathbf{\omega }}_{n+1}$，即周期结束时测量的角速度。用类似的方式在将${\mathbf{q}}_n$在$t_{n+1}$时刻泰勒展开，可以得到
$${\mathbf{q}}_n={\mathbf{q}}_{n+1}+{\dot{\mathbf{q}}}_{n+1}\left(-\Delta t\right)+\frac{1}{2!}{\ddot{\mathbf{q}}}_{n+1}{\left(-\Delta t\right)}^2+\frac{1}{3!}{\mathbf{q}}_{n+1}^{\left(3\right)}{\left(-\Delta t\right)}^3+\cdots$$
类似的，假设$\dot{\mathbf{\omega }}=0$
$${\mathbf{q}}_{n+1}^{(i)}={\mathbf{q}}_{n+1}\otimes (\frac{1}{2}{\mathbf{\omega }}_{n+1}{)}^i$$
于是
$$\begin{array}{rl}{\mathbf{q}}_n& ={\mathbf{q}}_{n+1}\otimes \left[\sum _{k=0}^{\infty }\frac{1}{k!}{\left(-\frac{1}{2}{\mathbf{\omega }}_{n+1}\Delta t\right)}^k\right]\\ & ={\mathbf{q}}_{n+1}\otimes \mathrm{Exp}(-{\mathbf{\omega }}_{n+1}\Delta t)\\ ⟹{\mathbf{q}}_{n+1}& ={\mathbf{q}}_n\otimes \mathrm{Exp}({\mathbf{\omega }}_{n+1}\Delta t)\end{array}$$
所以最终可得
q n + 1 ≈ q n ⊗ q { ω n + 1 Δ t } \bold{q}_{n+1}\approx \bold{q}_n\otimes \bold{q}\{\bm{\omega}_{n+1}\Delta t\} qn+1​≈qn​⊗q{ωn+1​Δt}
中点积分
类似的，认为周期$\Delta t$上的恒定角速度为中间角速度(不一定是周期中点角速度)
$$\bar{\mathbf{\omega }}=\frac{{\mathbf{\omega }}_n+{\mathbf{\omega }}_{n+1}}{2}$$
则有
q n + 1 ≈ q n ⊗ q { ω ˉ Δ t } \bold{q}_{n+1}\approx \bold{q}_n\otimes \bold{q}\{\bar{\bm{\omega}}\Delta t\} qn+1​≈qn​⊗q{ωˉΔt}