单源最短路径-Dijkstra算法

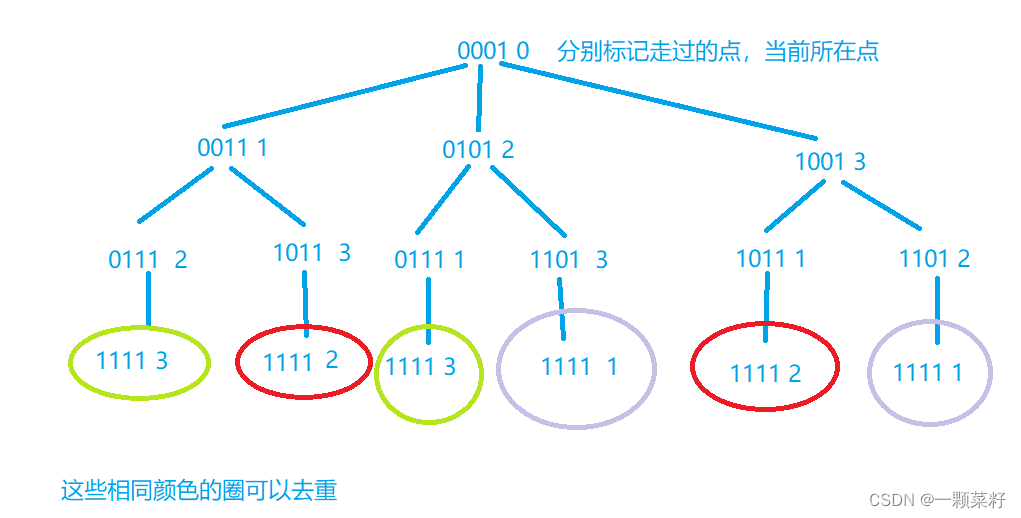
针对一个带权有向图G，将所有结点分为两组S和Q，S是已经确定最短路径的结点集合，在初始时为空（初始时就可以将源节点s放入，毕竟源节点到自己的代价是0），Q 为其余未确定最短路径的结点集合，每次从Q 中找出一个起点到该结点代价最小的结点u ，将u 从Q 中移出，并放入S 中，对u 的每一个相邻结点v 进行松弛操作。松弛即对每一个相邻结点v ，判断源节点s到结点u 的代价与u 到v 的代价之和是否比原来s 到v 的代价更小，若代价比原来小则要将s 到v 的代价更新为s 到u 与u 到v 的代价之和，否则维持原样。如此一直循环直至集合Q 为空，即所有节点都已经查找过一遍并确定了最短路径，至于一些起点到达不了的结点在算法循环后其代价仍为初始设定的值，不发生变化。

void Dijkstra(const V& src, vector<W>& dist, vector<int>& parentPath)
{
	int n = _vertexs.size();
	dist.resize(n,MAX_W);
	parentPath.resize(n, MAX_W);
	int srci = findIndex(src);
	
	parentPath[srci] = srci;
	dist[srci] = 0;
	vector<bool> minPath(n, false);
	
	for (int i = 0; i < n; i++)
	{
		// 找到最小的节点
		int mini = 0;
		int minW = MAX_W;
		for (int j = 0; j < n; j++)
		{
			if (minPath[j] == false && dist[j] < minW)
			{
				minW = dist[j];
				mini = j;
			}
		}

		minPath[mini] = true;
		//从最小的节点延伸出去
		for (int j = 0; j < n; j++)
		{
			// 从该节点延伸出去比员节点小
			if (_matrix[mini][j] != MAX_W && 
			dist[mini] + _matrix[mini][j] < dist[j])
			{
				dist[j] = dist[mini] + _matrix[mini][j];
				parentPath[j] = mini;
			}
		}
	}
}

缺点：Dijkstra算法无法解决带负权值的图

单源最短路径–Bellman-Ford算法

设i是src的一个中间节点，那么从src到j的最短路径p就被分成src到i和i到j的两段最短路径p1，p2。p1是从src到i且中间节点取得的一条最短路径。p2是从i到j且中间节点属于取得的一条最短路径。
i可以为src外的任意节点，因此进行k此后可以保证所得的结果是最小路径

bool BellmanFord(const V& src, vector<W>& dist, vector<int>& parentPath)
{
	int n = _vertexs.size();
	dist.resize(n, MAX_W);
	parentPath.resize(n, MAX_W);
	int srci = findIndex(src);

	parentPath[srci] = srci;
	dist[srci] = 0;
	vector<bool> minPath(n, false);

	for (int k = 0; k < n; k++)
	{
		bool exchange = false;
		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < n; j++)
			{
				// // srci->i + i->j < srci->j 则更新路径及权值 
				if (dist[i] != MAX_W && _matrix[i][j] != MAX_W && 
				dist[i] + _matrix[i][j] < dist[j])
				{
					dist[j] = dist[i] + _matrix[i][j];
					parentPath[j] = i;
					exchange = true;
				}
			}
		}
		if (exchange == false)
			break;
	}
	return true;
}

多源最短路径–Floyd-Warshall算法

与Bellman-Ford算法的大体思路类似-从单个节点改为了多个节点
设k是p的一个中间节点，那么从i到j的最短路径p就被分成i到k和k到j的两段最短路径p1，p2。p1是从i到k且中间节点属于{1，2，…，k-1}取得的一条最短路径。p2是从k到j且中间节点属于{1，2，…，k-1}取得的一条最短路径。

void FloydWarShall(vector<vector<W>>& vvDist, vector<vector<int>>& vvParentPath)
{
	int n = _vertexs.size();

	vvDist.resize(n, vector<W>(n, MAX_W));
	vvParentPath.resize(n, vector<int>(n, -1));


	for (int i = 0; i < n; i++)
	{
		vvDist[i][i] = W();
		vvParentPath[i][i] = i;
	}

	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			//i->j
			if (_matrix[i][j] != MAX_W)
			{
				vvDist[i][j] = _matrix[i][j];
				vvParentPath[i][j] = i;
			}
		}
	}

	for (int k = 0; k < n; k++)
	{
		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < n; j++)
			{

				//i->k + k->j < i->j 则更新路径及权值 
				if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W
					&& vvDist[i][k] + vvDist[k][j] < vvDist[i][j])
				{
					vvDist[i][j] = vvDist[i][k] + vvDist[k][j];
					vvParentPath[i][j] = vvParentPath[k][j];
				}
			}
		}
	}
}