缺失的第一个正数

news2025/7/13 8:57:13

题目链接

缺失的第一个正数

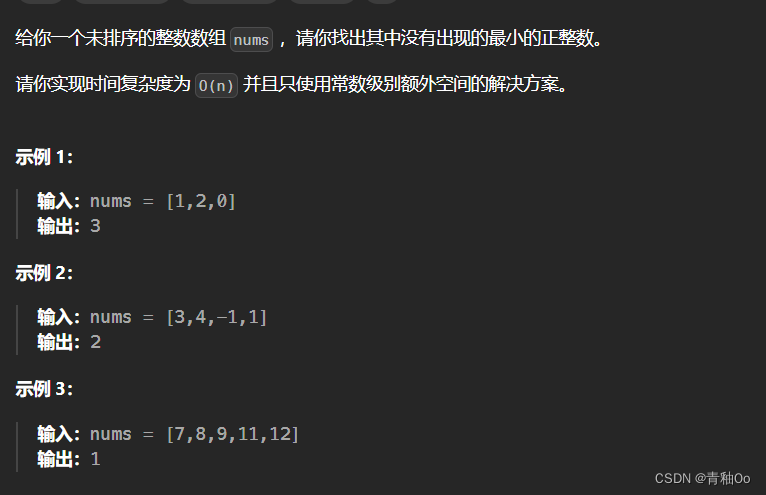
题目描述

注意点

实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案

解答思路

关键是要实现时间复杂度为 O(n) 并且只使用常数级别额外空间，需要将数字出现情况存储再原数组上，思路为：假设数组的长度为n，遍历整个数组，当遍历到数字任意i位置时，此时的元素值为prev = nums[i]，需要做以下操作：
- 如果prev的值等于i + 1，则不做任何操作直接跳出循环（prev值已经处于应该放置的位置）；如果prev的值不等于i + 1，此时需要将nums[prev - 1]与nums[i]的值进行交换（prev的值小于等于0或大于n时不考虑），也就是将prev值放在其应该放置的位置
- 在将nums[prev - 1]的值设置成新值prev时，此时nums[i]的值为oldNum，则还需要对oldNum做上面相同的操作，将nums[oldNum]继续与nums[i]的值进行交换，以此类推，直到遍历到的元素都处于其应该放置的位置
例子如下：
- 遍历到位置0：[3,4,-1,1] -> [-1,4,3,1]（数字3成功放置在下标2处）
- 遍历到位置1：[-1,4,3,1] -> [-1,1,3,4] -> [1,-1,3,4]（数字4成功放置在下标3，数字1成功放置在下标0）
- 遍历到位置2：[1,-1,3,4]
- 遍历到位置3：[1,-1,3,4]
当所有的元素都处于其应该放置的位置后，再次遍历整个数组，找到第一个nums[i] != i + 1的位置，也就是缺失的第一个正数，如果所有的位置上都正确放置了元素，说明缺失的第一个正数为nums.length + 1
需要注意的是，将某个值放在其应该放置的位置时，如果值小于等于0或大于n时可以不考虑，原因是：负数的情况不需要考虑；而如果是正数且该正数大于数组长度时，说明在该正数之前一定会有一个比其更小的正数缺失（否则数组的长度会大于n），其对寻找缺失的第一个正数也不会产生影响

代码

class Solution {
    public int firstMissingPositive(int[] nums) {
        int n = nums.length;
        // 使nums[i - 1] = i
        for (int i = 0; i < n; i++) {
            int prev = nums[i];
            while (prev - 1 >= 0 && prev - 1 < n && nums[prev - 1] != prev) {
                swap(nums, i, prev - 1);
                prev = nums[i];
            }
        }
        for (int i = 0; i < n; i++) {
            if (nums[i] != i + 1) {
                return i + 1;
            }
        }
        return n + 1;
    }

    public void swap(int[] nums, int left, int right) {
        int tmp = nums[left];
        nums[left] = nums[right];
        nums[right] = tmp;
    }
}