之前学习了很多的数据结构 有顺序表，堆，栈...

今天学习一种新的逻辑结构二叉树，他的物理结构是堆

让我们先简单回顾一下堆吧堆的简单介绍和一些简单功能的实现

1. 二叉树

其实堆就是一种特殊的数组，他的逻辑结构是二叉树

（逻辑结构和物理结构在上面的那片博客已经讨论过了，还有如何判断一个数组到底是不是堆

具体就是）

鉴于上面的博客已经帮大家入门了，今天来看一些更加进阶的问题

1.1建堆算法

比较推荐的是向下调整建堆

/*for (int i =1; i <n; i++) //向上调整建堆 O(N*logN)
	{
		AdjustUp(a, i);
	}*/
	for (int i = (n - 1 - 1) / 2; i >= 0; i--) //向下调整O(N)
	{
		AdjustDown(a,n, i);
	}

1.2堆排序

堆排就是利用堆这个数据结构来进行数据的排序

首先思考一个问题，现在要求升序到底是建大堆还是小堆

不要不假思索的说升序肯定是建小堆啊那你一定没有考虑

谁说小堆就是最小的数据在最上面依次排好的？

 

 

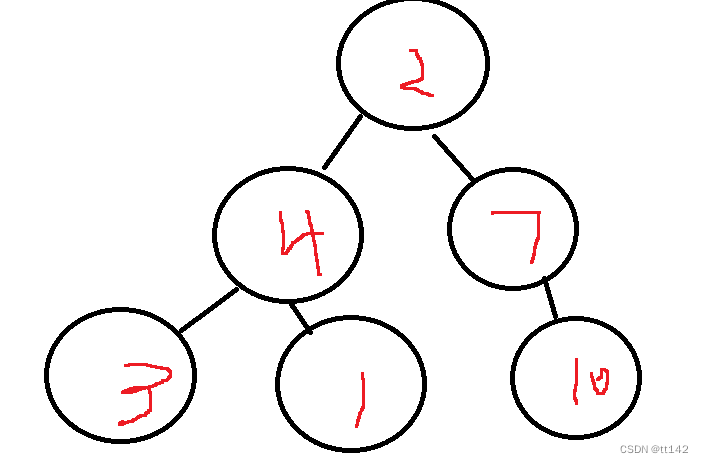
要是建小堆取出第一个数据之后整个堆的结构就没了你还那什么找第二小的数据？

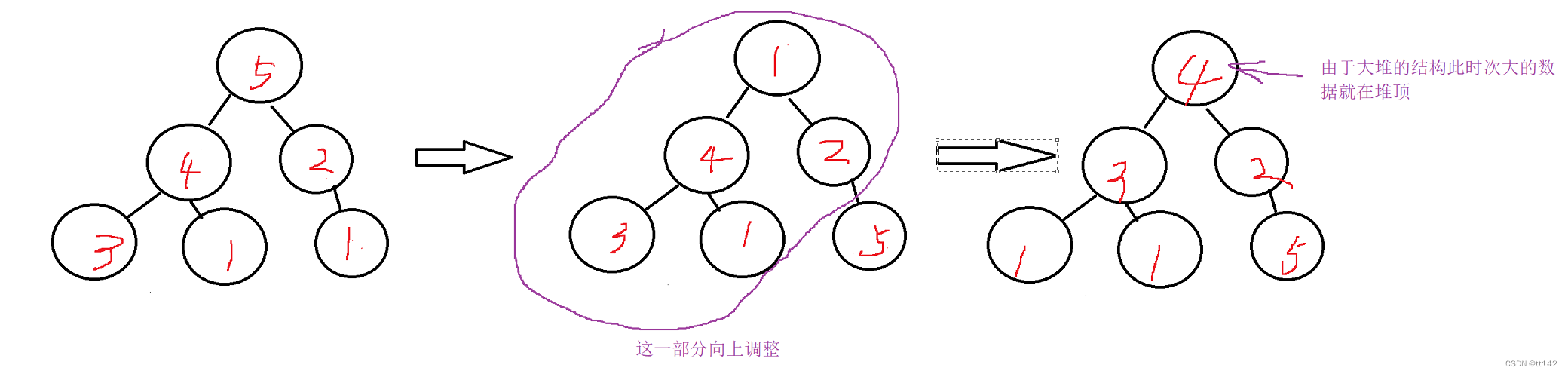
正确答案是建大堆，然后把堆顶的数据和最后一个数据交换，然后向下调整

因为由于大堆的数据结构，每次堆顶的数据一定是最大的，所以只要每次把堆顶的数据和最后一个数据换一下，那么就有一个数据已经归位了，只需要把最后一个已经归位的数据排除在外，其余数据向下调整就可以了，向上调整的时间复杂度是O(N*logN) 

void AdjustDown(HeapDataType* a, int n, int parent)
{
	assert(a);
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (a[child + 1] < a[child] && child+1<n)
		{
			child = child + 1;
		}
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
//1.堆排
void HeapSort(Hp* hp,HeapDataType* a,int n)
{
	assert(hp); 
	/*for (int i =1; i <n; i++) //向上调整建堆 O(N*logN)
	{
		AdjustUp(a, i);
	}*/
	for (int i = (n - 1 - 1) / 2; i >= 0; i--) //向下调整O(N)
	{
		AdjustDown(a,n, i);
	}
	//建好(大堆)之后要求升序（建大堆）
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);//把最大的数字放到最后
		AdjustDown(a, end, 0);
		end--;
	}
}

 1.3选出Topk

现实生活中我们不免有要找出排名前几的需求

只需要在上面堆排的基础上找出前几名或者后几名就可以了

HeapDataType HeapTop(Hp* hp)
{
	assert(hp);
	return hp->a[0]; //如果想找前三小的，刚才写的是升序那这里就应该依次返回堆顶的三个数据
}

但是不难发现这个写法效率实在太低，万一我有十亿个数据要找前五，无论空间还是时间上都是极大的浪费，所以我们还是建一个空间为k个数的小堆比较好

为什么这次就是小堆？

因为每次较小的数据就在堆顶，堆顶永远不可能是最大的数据，每次有更大的进来都会排出去一个较小的，直到最后所有较小的都被挤走了

void HeapTopk2(Hp* hp, int k)
{
	HeapDataType* Heapmin = (HeapDataType*)malloc(k * sizeof(HeapDataType));
	if (Heapmin == NULL)
	{
		perror("Heapmin malloc fail");
		exit(-1);
	}
	FILE* fout = fopen("Data.txt", "r");
	if (fout == NULL) {
		perror("fopen fail");
		exit(-1);
	}
	for (int i=0;i<k;i++)
	{
		fscanf(fout, "%d", &Heapmin[i]); //把数据都放到数组里面
	}
	//建小堆
	for (int i = (k - 1 - 1) / 2; i >= 0; i--) //向下调整O(N)
	{
		AdjustDown(Heapmin, k, i);
	}
	int val = 0;
	while (fscanf(fout, "%d", &val) != EOF)
	{
		if (val > Heapmin[0])
		{
			Heapmin[0] = val;
			AdjustDown(Heapmin, k, 0);

		}
	}
	for (int i = 0; i < k; i++)
	{
		printf("%d ", Heapmin[i]);
	}
	printf("\n");
	fclose(fout);
}