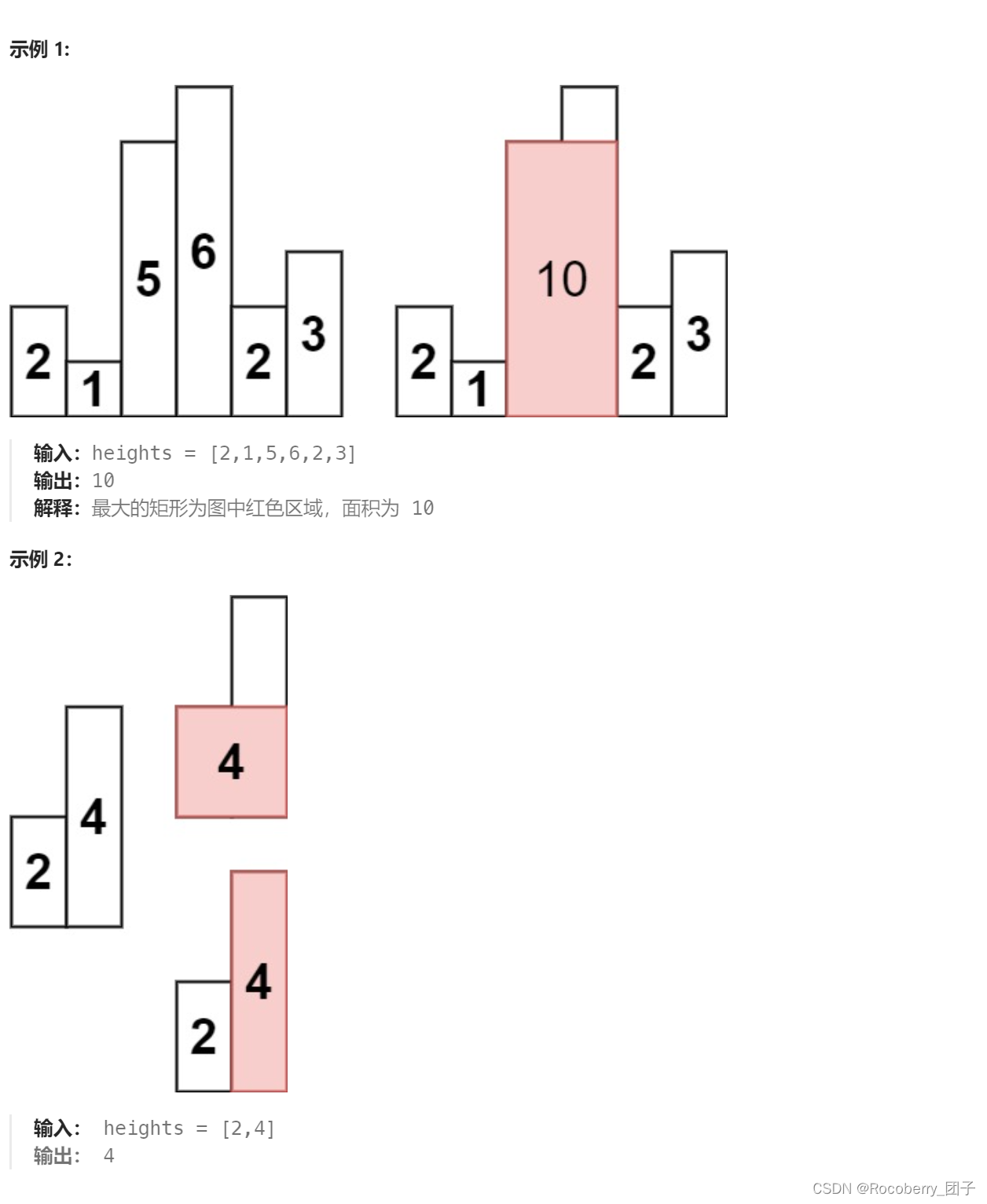
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

提示：

• 1 <= heights.length <= $10^5$
• 0 <= heights[i] <= $10^4$

类似接雨水（反过来，相当于找接雨水最少的一段）

题解1 暴力搜索（超时）$O(N^2)$

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int s = heights.size();
        int maxs = 0;
        for(int l = 0; l < s; l++){
            int minL = INT_MAX;
            for(int r = l; r < s; r++){
                minL = min(minL, heights[r]);
                maxs = max(maxs, minL*(r-l+1));
            }
        }
        return maxs;
    }
};

另一种

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int s = heights.size();
        int maxs = 0;
        for(int i = 0; i < s; i++){
            int l = i;
            int r = i;
            int tmph = heights[i];
            while(l >= 1 && heights[l-1] >= tmph)
                --l;
            while(r + 1 < s && heights[r+1] >= tmph)
                ++r;
            maxs = max(maxs, (r-l+1)*tmph);
        }
        return maxs;
    }
};

题解2 单调栈【重点学习】

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int s = heights.size();
        stack<int> stk; // 单调栈，下标对应值保持非严格递增
        vector<int> l(s, -1), r(s, s);
        int maxs = 0;
        // 从左向右
        // 找到离i最近的 < hegihts[i]的左边界
        for(int i = 0; i < s; i++){
            while(stk.size() && heights[stk.top()] >= heights[i])
                stk.pop();
            l[i] = (stk.empty() ? -1 : stk.top());
            stk.push(i);
        }
        stk = stack<int>();
        // 从右向左
        // 找到离i最近的 < hegihts[i]的右边界
        for(int i = s-1; i >= 0; i--){
            while(stk.size() && heights[stk.top()] >= heights[i])
                stk.pop();
            r[i] = (stk.empty() ? s : stk.top());
            stk.push(i);
        }
        for(int i = 0; i < s; i++){
        // 使用单调栈的初衷： 以height[i]为高度的矩形对应的宽 = r[i]-l[i]
            maxs = max(maxs, heights[i]*(r[i]-l[i]-1));
        }
        return maxs;
    }
};

常数优化

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int s = heights.size();
        stack<int> stk; // 单调栈，下标对应值保持非严格递增
        vector<int> l(s, -1), r(s, s);
        int maxs = 0;
        // 从左向右
        for(int i = 0; i < s; i++){
            while(stk.size() && heights[stk.top()] >= heights[i]){
                r[stk.top()] = i;
                stk.pop();
            }
                
            l[i] = (stk.empty() ? -1 : stk.top());
            stk.push(i);
        }
        
        for(int i = 0; i < s; i++){
            maxs = max(maxs, heights[i]*(r[i]-l[i]-1));
        }
        return maxs;
    }
};