摘要
利用二叉树的前序,中序,后序,有序数组来构建相关二叉树的问题。
一、构建二叉树题目
105. 从前序与中序遍历序列构造二叉树
106. 从中序与后序遍历序列构造二叉树
889. 根据前序和后序遍历构造二叉树
617. 合并二叉树
226. 翻转二叉树
109. 有序链表转换二叉搜索树
二、构建二叉树问题详解
2.1 前序中序构建二叉树

package Tree;
import java.util.HashMap;
/**
* @BelongsProject: SeniorArchitect-LeetCode
* @BelongsPackage: Tree
* @Author: zhuangxiaoyan
* @CreateTime: 2023-10-25 07:24
* @Description: TODO
* @Version: 1.0
*/
public class 前序中序构建二叉树105 {
// 给定的前序和中序遍历构建一个二叉树
public TreeNode buildTree(int[] preorder, int[] inorder) {
int prelen = preorder.length;
int inlen = inorder.length;
if (prelen != inlen) {
throw new RuntimeException("Imcorrent input data");
}
HashMap<Integer, Integer> map = new HashMap<>();
// 遍历一次中序遍历
for (int i = 0; i < inlen; i++) {
map.put(inorder[i], i);
}
// 然后递归调用
return buildTree2(preorder, 0, prelen - 1, map, 0, inlen - 1);
}
private TreeNode buildTree2(int[] preorder, int preleft, int preright, HashMap<Integer, Integer> map, int inleft, int inright) {
// 递归的终止条件
if (preleft > preright || inleft > inright) {
return null;
}
int rootvalue = preorder[preleft];
TreeNode root = new TreeNode(rootvalue);
// 获取标
int pIndex = map.get(rootvalue);
root.left = buildTree2(preorder, preleft + 1, pIndex - inleft + preleft, map, inleft, pIndex - 1);
root.right = buildTree2(preorder, pIndex - inleft + preleft + 1, preright, map, pIndex + 1, inright);
return root;
}
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
}
时间与空间复杂度分析
- 时间复杂度:O(n) 最坏的情况就是最左(右)子树 那就需要遍历n-1个元素。
- 空间复杂度:O(1)不需要其他的额外空间来存储元素。
2.2 中序后续构建二叉树

package Tree;
import java.util.HashMap;
/**
* @BelongsProject: SeniorArchitect-LeetCode
* @BelongsPackage: Tree
* @Author: zhuangxiaoyan
* @CreateTime: 2023-10-25 07:25
* @Description: TODO
* @Version: 1.0
*/
public class 后序中序构建二叉树106 {
public TreeNode buildTree(int[] inorder, int[] postorder) {
int inlen = inorder.length;
int postlen = postorder.length;
if (inlen != postlen) {
throw new RuntimeException("Incurrent input data");
}
HashMap<Integer, Integer> hashMap = new HashMap<>();
for (int i = 0; i < inlen; i++) {
hashMap.put(inorder[i], i);
}
return buildTree2(postorder, 0, postlen - 1, hashMap, 0, inlen - 1);
}
private TreeNode buildTree2(int[] postorder, int postleft, int postright, HashMap<Integer, Integer> hashMap, int inleft, int inright) {
if (postleft > postright || inleft > inright) {
return null;
}
int rootval = postorder[postright];
TreeNode root = new TreeNode(rootval);
int pIndex = hashMap.get(rootval);
root.left = buildTree2(postorder, postleft, pIndex - inleft + postleft - 1, hashMap, inleft, pIndex - 1);
root.right = buildTree2(postorder, pIndex - inleft + postleft, postright - 1, hashMap, pIndex + 1, inright);
return root;
}
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
}
时间与空间复杂度分析
- 时间复杂度:O(n) 最坏的情况就是最左(右)子树 那就需要遍历n-1个元素。
- 空间复杂度:O(1)不需要其他的额外空间来存储元素。
2.3 前序后序构建二叉树

- 前序遍历的结果是[1,2,4,5,3,6,7]
- 后序遍历的结果是[4,5,2,6,7,3,1]
- 前序遍历的特点是根节点始终出现在第一位
- 后序遍历的特点是根节点始终出现在最后一位
但是,你会发现仅仅用这些条件还不够,虽然能很快确定根节点了,但是根节点的左子树的范围就没法确定,没法确定左子树范围,也会导致右子树也确定不了。
我们先回顾一下二叉树的前序、后序遍历
二叉树的前序遍历是:
- 打印根节点
- 遍历左子树
- 遍历右子树
二叉树的后序遍历是:
- 遍历左子树
- 遍历右子树
- 打印根节点

前序遍历第一个元素是根节点,后面的那一堆就是左子树,接着是右子树,而后序遍历第一个出现的是左子树,然后是右子树,最后才是根节点,上图中我用橙色标记出了左子树部分,用绿色标记出了右子树部分。
两种遍历方式得到的橙色部分数量是一样的,绿色部分数量也是一样的。所以,我们只要能确定橙色部分的范围,就可以处理左子树了,而左子树范围确定了,那么顺带右子树也就可以搞定了。

- 如果遍历这个左子树
- 前序遍历的结果是[2,4,5]
- 后序遍历的结果是[4,5,2]
我们根据2就可以确定出后序遍历的左子树范围 因为后序遍历的整棵树的结果是[4,5,2,6,7,3,1]
现在我们找到2了,根节点的位置是固定出现在最后的,那么右子树的范围也就可以确定了。
后序遍历数组下标是从0开始的,我们确定了2的位置,还需要+1,这样就得到了整个左子树的个数。
总结一下
- 用前序遍历的第一个元素创建出根节点
- 用前序遍历的第二个元素x,去后序遍历中找对应的下标y,将y+1就能得到左子树的个数了
- 将前序数组,后序数组拆分左右两部分
- 递归的处理前序数组左边、后序数组右边
- 递归的处理前序数组右边、后序数组右边
- 返回根节点
拆分的规则如下(假设得到的左子树数量为left_count)
拆分的前序数组:
- 左半部分[1,left_count+1)
- 右半部分[left_count+1,N)
拆分的后序数组:
- 左半部分[0,left_count)
- 右半部分[left_count,N-1)
package Tree;
import org.junit.Test;
import java.util.Arrays;
/**
* @BelongsProject: SeniorArchitect-LeetCode
* @BelongsPackage: Tree
* @Author: zhuangxiaoyan
* @CreateTime: 2023-10-31 20:55
* @Description: TODO
* @Version: 1.0
*/
public class 前序后序构建二叉树 {
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
public TreeNode constructFromPrePost(int[] pre, int[] post) {
if(pre==null || pre.length==0) {
return null;
}
return dfs(pre,post);
}
private TreeNode dfs(int[] pre,int[] post) {
if(pre==null || pre.length==0) {
return null;
}
//数组长度为1时,直接返回即可
if(pre.length==1) {
return new TreeNode(pre[0]);
}
//根据前序数组的第一个元素,创建根节点
TreeNode root = new TreeNode(pre[0]);
int n = pre.length;
for(int i=0;i<post.length;++i) {
if(pre[1]==post[i]) {
//根据前序数组第二个元素,确定后序数组左子树范围
int left_count = i+1;
//拆分前序和后序数组,分成四份
int[] pre_left = Arrays.copyOfRange(pre,1,left_count+1);
int[] pre_right = Arrays.copyOfRange(pre,left_count+1,n);
int[] post_left = Arrays.copyOfRange(post,0,left_count);
int[] post_right = Arrays.copyOfRange(post,left_count,n-1);
//递归执行前序数组左边、后序数组左边
root.left = dfs(pre_left,post_left);
//递归执行前序数组右边、后序数组右边
root.right = dfs(pre_right,post_right);
break;
}
}
//返回根节点
return root;
}
}
时间与空间复杂度分析
- 时间复杂度:O(n) 最坏的情况就是最左(右)子树 那就需要遍历n-1个元素。
- 空间复杂度:O(1)不需要其他的额外空间来存储元素。
2.4 合并二叉树

package Tree;
/**
* @BelongsProject: SeniorArchitect-LeetCode
* @BelongsPackage: Tree
* @Author: zhuangxiaoyan
* @CreateTime: 2023-10-31 22:50
* @Description: TODO
* @Version: 1.0
*/
public class 合并二叉树617 {
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
if (root1 == null && root2 == null) {
return null;
}
if (root1 == null && root2 != null) {
return root2;
}
if (root1 != null && root2 == null) {
return root1;
}
// 都是kong
root1.val += root2.val;
root1.left = mergeTrees(root1.left, root2.left);
root1.right = mergeTrees(root1.right, root2.right);
return root1;
}
}
时间与空间复杂度分析
- 时间复杂度:O(n) 最坏的情况就是遍历二叉树所有元素。
- 空间复杂度:O(1)不需要其他的额外空间来存储元素。
2.5 有序数组构建二叉树

package Tree;
/**
* @BelongsProject: SeniorArchitect-LeetCode
* @BelongsPackage: Tree
* @Author: zhuangxiaoyan
* @CreateTime: 2023-10-26 08:25
* @Description: TODO
* @Version: 1.0
*/
public class 有序数组构建二叉搜索树108 {
public TreeNode sortedArrayToBST(int[] nums) {
if (nums.length < 1) {
return new TreeNode();
}
if (nums.length == 1) {
return new TreeNode(nums[0]);
}
TreeNode root = buildTree(nums, 0, nums.length - 1);
return root;
}
private TreeNode buildTree(int[] nums, int left, int right) {
if (left > right) {
return null;
}
int mid = left + (right - left) / 2;
TreeNode root = new TreeNode(nums[mid]);
root.left = buildTree(nums, left, mid - 1);
root.right = buildTree(nums, mid + 1, right);
return root;
}
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
}
时间与空间复杂度分析
- 时间复杂度:O(n) 最坏的情况就是二叉树所有的元素。
- 空间复杂度:O(1)不需要其他的额外空间来存储元素。
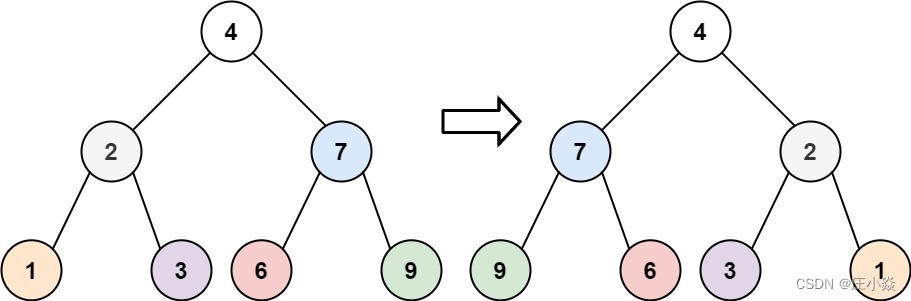
2.6 翻转二叉树
package Tree;
/**
* @BelongsProject: SeniorArchitect-LeetCode
* @BelongsPackage: Tree
* @Author: zhuangxiaoyan
* @CreateTime: 2023-10-24 22:47
* @Description: TODO
* @Version: 1.0
*/
public class 二叉树翻转226 {
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return root;
}
// 交换左右子树
TreeNode tmp = root.right;
root.right = root.left;
root.left = tmp;
// 递归的调用左右子树
invertTree(root.left);
invertTree(root.right);
return root;
}
public TreeNode invertTree2(TreeNode root) {
if (root == null) {
return root;
}
// 递归左右的遍历
invertTree(root.left);
invertTree(root.right);
// 中遍历
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
return root;
}
public TreeNode invertTree3(TreeNode root) {
if (root == null) {
return root;
}
// 递归左右的遍历
invertTree3(root.left);
// 中遍历
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
invertTree3(root.left); // 注意 这里依然要遍历左孩子,因为中间节点已经翻转了
return root;
}
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
}
时间与空间复杂度分析
- 时间复杂度:O(n) 最坏的情况就是遍历所有元素。
- 空间复杂度:O(1)不需要其他的额外空间来存储元素。
博文参考
https://leetcode.cn/circle/discuss/E3yavq/#%E6%A0%91%E4%B8%8E%E4%BA%8C%E5%8F%89%E6%A0%91%E7%AF%87