一、扫地机器人的示例

        我们可以明确给出扫地机器人的Bellman最优方程。为了使问题更简洁，我们将状态高和低以及动作搜索、等待和充电分别缩写为h、l、s、w和re。由于只有两个状态，Bellman最优方程由两个方程组成。v∗(h)的方程可以写成：

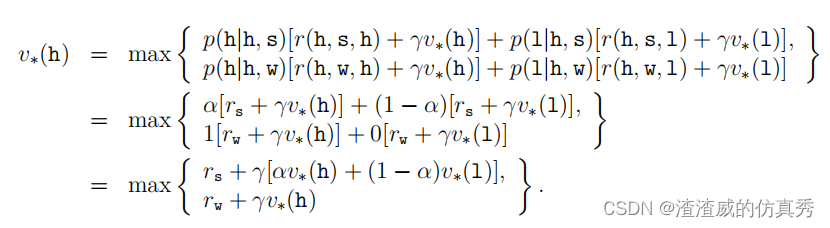
按照前面相同的步骤，得到v∗(l)的方程为

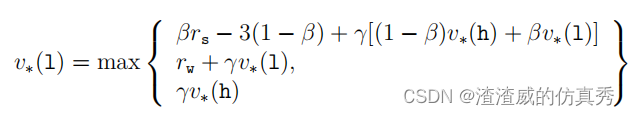
对于任何选择的rs，rw，α，β和γ，其中0 ≤ γ < 1，0 ≤ α，β ≤ 1，存在恰好一对数字v∗(h)和v∗(l)，同时满足这两个非线性方程。

二、Gridworld的示例

        假设我们解决了Bellman方程的v∗，对于在Gridworld中引入并再次在图1a中展示的简单网格任务。请记住，状态A后面跟着+10的奖励和到状态A0的转换，而状态B后面跟着+5的奖励和到状态B0的转换。图1b显示了最优值函数，图1c显示了相应的最优策略。在单元格中有多个箭头表示，任何相应的动作都是最佳的。

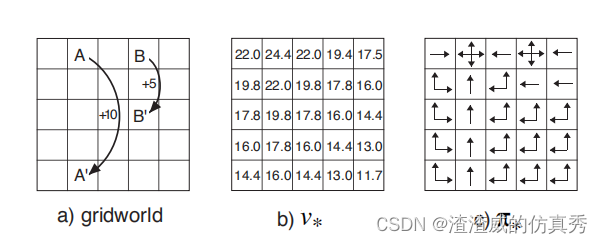
图1

        显式地解决Bellman最优性方程提供了一种找到最优策略的途径，从而解决了强化学习问题。然而，这个解决方案很少直接有用。它类似于一个全面的搜索，前瞻性地看待所有可能性，计算它们发生的概率以及它们在预期奖励方面的适宜性。这个解决方案依赖于至少三个在实践中很少成立的假设：(1) 我们准确地知道环境的动态；(2) 我们有足够的计算资源来完成计算的解决方案；(3)马尔可夫属性。对于我们感兴趣的任务类型，一个人通常不能准确地实现这种解决方案，因为这些假设的各种组合是不成立的。例如，虽然第一个和第三个假设对双陆棋游戏没有造成问题，但第二个假设是一个主要的障碍。由于游戏有大约1020个状态，因此在当今最快的计算机上解决v∗的Bellman方程将需要数千年的时间，同样的情况也适用于寻找q∗。在强化学习中，通常需要求助于近似解。

        许多不同的决策制定方法可以看作是近似求解Bellman最优方程的方法。例如，启发式搜索方法可以看作是将（3.17）的右侧展开几次，达到一定的深度，形成一个“树”的可能性，然后使用启发式评估函数来近似v∗的“叶子”节点。启发式搜索方法如A∗几乎总是基于离散情况。动态规划的方法与Bellman最优方程的关系更为密切。许多强化学习方法可以清楚地理解为近似求解Bellman最优方程，用实际的经验转移代替期望转移的知识。后续将考虑各种这样的方法。