62.不同路径

力扣题目链接
题目描述：
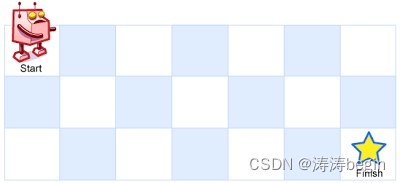
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。
问总共有多少条不同的路径？

示例 1：

输入：m = 3, n = 7
输出：28

思路：

• 这道题是换成二维数组来表示dp，因为每个位置只能由上边和左边格子走过去，所以每个格子的路径数就是上面格子和左面格子之和。
• 动态规划五部曲：
  1. 分析好dp数组代表什么：dp[ i ][ j ]代表二维数组每个位置，从起点到这个位置的路径数目
  2. 分析 dp 推导式：dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
  3. 根据dp推导式，初始化dp数组：因为第一行只能由左边格子走到，第一列只能由上边位置走到，所以，初始化第一列和第一行元素为1。
  4. 确定遍历顺序：双层for循环，从第二行和第二列开始（i，j都是1），不断计算出每个格子的路径数，最后一次就算出到终点的路径总数了。
  5. 根据dp数组输出，判断是否符合预期

代码实现：

int uniquePaths(int m, int n) {
        //dp[m][n] = dp[m - 1][n] + dp[m][n - 1];
        vector<vector<int>> dp(m, vector<int>(n));
        dp[0] = vector<int>(n , 1);
        for (int i = 1; i < m; ++i) {
            dp[i][0] = 1;
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }

63. 不同路径 II

力扣题目链接
题目描述：
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？
网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：

1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

思路：

• 这道题和上题类似，同样是换成二维数组来表示dp，区别是增加了障碍，那遇到初始化的时候就得改变了，只要第一行和第一列有障碍物，那么后序的格子都到不了了，另外计算中间元素的时候也是，如果是障碍物，直接跳过就可以了（定义数组的时候都初始化为0了）。
• 动态规划五部曲：
  1. 分析好dp数组代表什么：dp[ i ][ j ]代表二维数组每个位置，从起点到这个位置的路径数目
  2. 分析 dp 推导式：状态转移公式不变：dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
  3. 根据dp推导式，初始化dp数组：因为第一行只能由左边格子走到，第一列只能由上边位置走到，所以，初始化第一列和第一行元素为1，但是遇到障碍物就直接退出循环。
  4. 确定遍历顺序：双层for循环，从第二行和第二列开始（i，j都是1），不断计算出每个格子的路径数，最后一次就算出到终点的路径总数了。
  5. 根据dp数组输出，判断是否符合预期

** 代码实现：**

• 自己写的

int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        //dp[m][n] = dp[m - 1][n] + dp[m][n - 1];
        int m = obstacleGrid.size(), n = obstacleGrid[0].size();
        vector<vector<int>> dp(m, vector<int>(n));
        for (int i = 0; i < n; ++i) {
            if (obstacleGrid[0][i]) {
                while(i < n)    dp[0][i++] = 0;
                break;
            }
            dp[0][i] = 1;
        }
        for (int i = 0; i < m; ++i) {
            if (obstacleGrid[i][0]) {
                while(i < m)    dp[i++][0] = 0;
                break;
            }
            dp[i][0] = 1;
        }
        int left = 0, up = 0;
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                if (obstacleGrid[i][j]) {
                     dp[i][j] = 0;
                } else {
                    left = obstacleGrid[i][j - 1] == 1 ? 0 : dp[i][j - 1];
                    up = obstacleGrid[i - 1][j] == 1 ? 0 : dp[i - 1][j];
                    dp[i][j] = left + up;
                }
                
            }
        }
        return dp[m - 1][n - 1];
    }

• 优化：
  1. 注意初始化的代码写法，可以把判断移到for循环判断里
  2. 增加了当起点和终点为1时，直接return，假如是终点为障碍，这样就不用计算整个数组了，直接退出。
  3. 双层for循环逻辑太麻烦，完全可以简化。

int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        //dp[m][n] = dp[m - 1][n] + dp[m][n - 1];
        int m = obstacleGrid.size(), n = obstacleGrid[0].size();
        if (obstacleGrid[0][0] || obstacleGrid[m - 1][n - 1])   return 0;
        vector<vector<int>> dp(m, vector<int>(n, 0));
        for (int i = 0; i < n && obstacleGrid[0][i] == 0; ++i) {
            dp[0][i] = 1;
        }
        for (int i = 0; i < m && obstacleGrid[i][0] == 0; ++i) {
            dp[i][0] = 1;
        }
        int left = 0, up = 0;
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                if (obstacleGrid[i][j] == 0) {
                    dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
                }
            }
        }
        return dp[m - 1][n - 1];
    }

980. 不同路径 III

• 这道题用回溯法做！