目录
- 一.高中
- 二.高数基础
- 三.高数
- 第一章 空间解析几何与向量代数
- 2.向量代数
- 6.二次曲面
- 第二章 多元函数的微分学
- 第三章 重积分
- 一、二重积分
- 二、 三重积分
- 直角坐标下三重积分的计算
- 柱面坐标下三重积分的计算
- 球面坐标下三重积分的计算
- 曲面面积
- 第四章 曲线积分与曲面积分
- 1、对弧长的曲线积分
- 2、对坐标的曲线积分
- 3、格林公式
- 4、对面积的曲线积分
- 5、对坐标的曲线积分
- 第六章 无穷级数
- 一、数项级数的审敛法
- 1、常数项级数
- 2、正项级数
- 3、交错级数
- 4、任意项级数
- 二、幂级数
- 三、函数的幂级数展开式
- 四、傅里叶幂级数
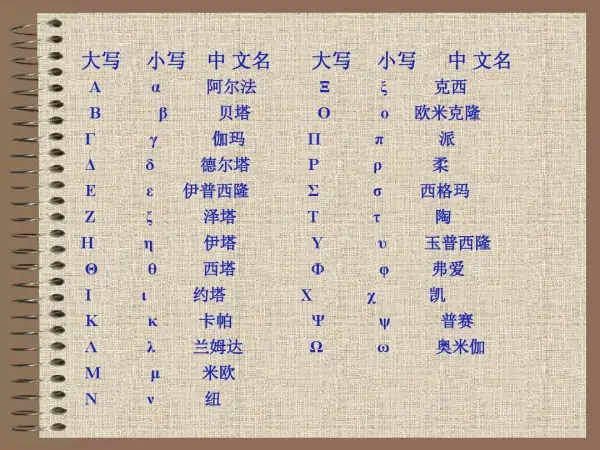
数学符号
一.高中
-
整式的乘法运算
a m ⋅ a n = a m + n a^m \cdot a^n = a^{m+n} am⋅an=am+n
a m ÷ a n = a m − n a^m \div a^n = a^{m-n} am÷an=am−n
( a m ) n = a m ⋅ n (a ^m)^n =a^{m \cdot n} (am)n=am⋅n
( a b ) n = a n b n (ab)^n =a^nb^n (ab)n=anbn -
常用的乘法公式
平方差公式: ( a + b ) ( a − b ) = a 2 − b 2 (a+b)(a-b)=a^2-b^2 (a+b)(a−b)=a2−b2
完全平方公式: ( a ± b ) 2 = a 2 ± 2 a b + b 2 (a \pm b)^2=a^2 \pm 2ab+b^2 (a±b)2=a2±2ab+b2 -
一元二次方程
方程的形式: a x 2 + b x + c = 0 ( a ≠ 0 ) ax^2+bx+c=0(a \ne 0) ax2+bx+c=0(a=0)
求根公式: − b ± b 2 − 4 a c 2 a \cfrac{-b \pm \sqrt {b^2-4ac}}{2a} 2a−b±b2−4ac
x 1 + x 2 = − b a , x 1 x 2 = c a x_1+x_2=-\cfrac{b}{a} , x_1x_2=\cfrac{c}{a} x1+x2=−ab,x1x2=ac -
指数函数
(1)正分数指数幂: a m n = a m n a^{\frac{m}{n}}= \sqrt[n]{a^m} anm=nam,( a ≥ 0 , m a \ge 0,m a≥0,m、 n ∈ N n \in N n∈N且 n > 1 , m n > 1,m n>1,m、 n n n互质)
(2)幂的运算法则
a m ⋅ a n = a m + n a^m \cdot a^n = a^{m+n} am⋅an=am+n
a m ÷ a n = a m − n a^m \div a^n = a^{m-n} am÷an=am−n
( a m ) n = a m ⋅ n (a^m)^n = a^{m \cdot n} (am)n=am⋅n
( a b ) n = a n b n (ab)^n = a^{n}b^{n} (ab)n=anbn
( a b ) n = a n b n = a n ⋅ b − n (\cfrac{a}{b})^n = \cfrac{a^n}{b^n} =a^n \cdot b^{-n} (ba)n=bnan=an⋅b−n -
对数函数
(2)性质:
log a a = 1 \log_a{a}=1 logaa=1
log a 1 = 0 \log_a{1}=0 loga1=0
0和负数无对数
a log a N = N a^{\log_a{N}}=N alogaN=N
(3)运算法则:
log a ( M ⋅ N ) = log a M + log a N \log_a(M \cdot N) = \log_a{M} + \log_a{N} loga(M⋅N)=logaM+logaN
log a ( M N ) = log a M − log a N \log_a(\cfrac{M}{N}) = \log_a{M} - \log_a{N} loga(NM)=logaM−logaN
log a m b n = n m ⋅ log a b \log_{a^m}b^n = \cfrac{n}{m}\cdot \log_a{b} logambn=mn⋅logab
(4)换底公式: log a N = log b N log b a \log_aN = \cfrac{\log_bN}{\log_ba} logaN=logbalogbN -
三角函数
(1)同角三角函数的基本关系式
平方关系: sin 2 x + cos 2 x = 1 \sin^2x + \cos^2 x =1 sin2x+cos2x=1
(2)两角和与差的三角函数
sin ( α ± β ) = sin α cos β ± cos α sin β \sin(\alpha \pm \beta) = \sin\alpha \cos\beta \pm \cos\alpha \sin\beta sin(α±β)=sinαcosβ±cosαsinβ
cos ( α ± β ) = cos α cos β ∓ sin α sin β \cos(\alpha \pm \beta) = \cos\alpha \cos\beta \mp \sin\alpha \sin\beta cos(α±β)=cosαcosβ∓sinαsinβ
tan ( α ± β ) = tan α ± tan β 1 ∓ tan α tan β \tan(\alpha \pm \beta) = \cfrac{\tan\alpha \pm \tan\beta}{1 \mp \tan\alpha\tan\beta} tan(α±β)=1∓tanαtanβtanα±tanβ
(3)三角函数的倍角公式
sin ( 2 α ) = 2 sin α cos α \sin(2\alpha) = 2\sin\alpha \cos\alpha sin(2α)=2sinαcosα
cos ( 2 α ) = cos 2 α − sin 2 α = 2 cos 2 α − 1 = 1 − 2 sin 2 α \cos(2\alpha) = \cos^2\alpha - \sin^2\alpha =2\cos^2\alpha-1 = 1-2\sin^2\alpha cos(2α)=cos2α−sin2α=2cos2α−1=1−2sin2α
tan ( 2 α ) = 2 tan α 1 − tan 2 α \tan(2\alpha) = \cfrac{2\tan\alpha}{1 - \tan^2\alpha} tan(2α)=1−tan2α2tanα
(4) 特殊的三角函数值度 0 ° 0 \degree 0° 30 ° 30 \degree 30° 45 ° 45 \degree 45° 60 ° 60 \degree 60° 90 ° 90 \degree 90° 180 ° 180 \degree 180° 270 ° 270 \degree 270° 360 ° 360 \degree 360° 弧度 0 π 6 \cfrac{\pi}{6} 6π π 4 \cfrac{\pi}{4} 4π π 3 \cfrac{\pi}{3} 3π π 2 \cfrac{\pi}{2} 2π π \pi π 3 π 2 \cfrac{3\pi}{2} 23π 2 π 2\pi 2π sin α \sin \alpha sinα 0 1 2 \cfrac{1}{2} 21 2 2 \cfrac{\sqrt2}{2} 22 3 2 \cfrac{\sqrt3}{2} 23 1 0 -1 0 cos α \cos \alpha cosα 1 3 2 \cfrac{\sqrt3}{2} 23 2 2 \cfrac{\sqrt2}{2} 22 1 2 \cfrac{1}{2} 21 0 -1 0 1 tan α \tan \alpha tanα 0 3 3 \cfrac{\sqrt3}{3} 33 1 1 1 3 \sqrt3 3 - 0 - 0 -
等差数列
(1)通项公式: a n = a 1 + ( n − 1 ) d a_n = a_1+(n-1)d an=a1+(n−1)d
(2)等差数列前n项和: S n = n ( a 1 + a n ) 2 S_n = \cfrac{n(a_1+a_n)}{2} Sn=2n(a1+an) 或者 S n = n a 1 + n ( n − 1 ) d 2 S_n = na_1+\cfrac{n(n-1)d}{2} Sn=na1+2n(n−1)d -
等比数列
(1)通项公式: a n = a 1 q n − 1 a_n = a_1q^{n-1} an=a1qn−1,中项: b 2 = a c b^2 = ac b2=ac
(2)等比数列的前n项和: S n = { n a 1 , q = 1 a 1 ( 1 − q n ) 1 − q 或者 a 1 − a n q 1 − q , q ≠ 1 S_n = \begin{cases}na_1, q=1 \\ \cfrac{a_1(1-q^n)}{1-q} 或者 \cfrac{a_1-a_nq}{1-q},q \ne 1\end{cases} Sn=⎩ ⎨ ⎧na1,q=11−qa1(1−qn)或者1−qa1−anq,q=1 -
向量的坐标运算
向量的长度及两点间的距离公式
设 A = ( x 1 , y 1 ) , B = ( x 2 , y 2 ) A =(x_1,y_1),B =(x_2,y_2) A=(x1,y1),B=(x2,y2)
长度: ∣ A ∣ = x 1 2 + x 2 2 |A| = \sqrt{x_1{^2}+x_2{^2}} ∣A∣=x12+x22
距离: d A B = ∣ A B → ∣ = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 d_{AB}= |\overrightarrow {AB}| = \sqrt{(x_2 - x_1){^2}+(y_2 - y_1){^2}} dAB=∣AB∣=(x2−x1)2+(y2−y1)2 -
向量的数量积
(1)向量a,b的数量积: a ⋅ b = ∣ a ∣ ∣ b ∣ cos ⟨ a , b ⟩ a \cdot b = |a||b| \cos \lang a,b \rangle a⋅b=∣a∣∣b∣cos⟨a,b⟩
(2)向量数量积的运算:
在坐标平面 O x y Oxy Oxy中,已知 a = ( x 1 , y 1 ) , b = ( x 2 , y 2 ) a = (x_1,y_1),b = (x_2,y_2) a=(x1,y1),b=(x2,y2)
性质:
a ⊥ b ⟺ x 1 x 2 + y 1 y 2 = 0 a \bot b \iff x_1x_2+y_1y_2 = 0 a⊥b⟺x1x2+y1y2=0
a ∥ b ⟺ x 1 x 2 = y 1 y 2 a \parallel b \iff \cfrac{x_1}{x_2} =\cfrac{y_1}{y_2} a∥b⟺x2x1=y2y1 -
直线
(1)斜率:直线倾斜角 α ( α ≠ 90 ° ) \alpha(\alpha \ne 90 \degree) α(α=90°)的正切值,用 k k k表示,即 k = tan α k=\tan \alpha k=tanα。
一般形式:给定 P 1 ( x 1 , y 1 ) , P 2 ( x 2 , y 2 ) P_1(x_1,y_1),P_2(x_2,y_2) P1(x1,y1),P2(x2,y2)是直线上任意两点,斜率 k = y 2 − y 1 x 2 − x 1 ( x 2 ≠ x 1 ) k=\cfrac{y_2-y_1}{x_2-x_1}(x_2 \ne x_1) k=x2−x1y2−y1(x2=x1)
(2)直线方程的形式名称 已知条件 方程形式 说明 斜截式 斜率 k k k和直线在 y y y轴上的截距 b b b y = k x + b y=kx+b y=kx+b 不包括y轴和平行 y y y轴的直线 点斜式 直线过点 P 1 ( x 1 , y 1 ) P_1(x_1,y_1) P1(x1,y1)和斜率 k k k y − y 1 = k ( x − x 1 ) y-y_1=k(x-x_1) y−y1=k(x−x1) 不包括y轴和平行 y y y轴的直线 两点式 直线过点 P 1 ( x 1 , y 1 ) , P 2 ( x 2 , y 2 ) P_1(x_1,y_1),P_2(x_2,y_2) P1(x1,y1),P2(x2,y2) ( x 1 ≠ x 2 , y 1 ≠ y 2 ) (x_1 \ne x_2,y_1\ne y_2) (x1=x2,y1=y2) y − y 1 y 2 − y 1 = x − x 1 x 2 − x 1 \cfrac{y-y1}{y_2-y_1}=\cfrac{x-x_1}{x_2-x_1} y2−y1y−y1=x2−x1x−x1 不包括坐标轴和平行坐标轴的直线 截距式 直线在 x x x轴上的截距是 a ( a ≠ 0 ) a(a \ne 0) a(a=0)
直线在 y y y轴上的截距是 b ( b ≠ 0 ) b(b \ne 0) b(b=0)x a + y b = 1 \cfrac{x}{a}+\cfrac{y}{b}=1 ax+by=1 不包括经过原点的直线和平行坐标轴的直线 一般式 A , B A,B A,B不同时为零 A x + B y + C = 0 ( k = − A B ) Ax+By+C=0(k=-\cfrac{A}{B}) Ax+By+C=0(k=−BA) 任何直线都可写成此形式
(3)两直线的位置关系
设两直线的斜率都存在,其方程分别为:
{
l
1
:
y
=
k
1
x
+
b
1
l
2
:
y
=
k
2
x
+
b
2
\begin{cases} l_1: y=k_1x+b1 \\ l_2: y=k_2x+b2 \end{cases}
{l1:y=k1x+b1l2:y=k2x+b2
两直线平行:
k
1
=
k
2
k_1=k_2
k1=k2
两直线垂直:
k
1
k
2
=
−
1
k_1k_2=-1
k1k2=−1
(4)点到直线的距离:设点
P
1
(
x
0
,
y
0
)
P_1(x_0,y_0)
P1(x0,y0)到直线
A
x
+
B
y
+
C
=
0
Ax+By+C=0
Ax+By+C=0,则有
d
=
∣
A
x
0
+
B
y
0
+
C
∣
A
2
+
B
2
d = \cfrac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}
d=A2+B2∣Ax0+By0+C∣
(5)两平行线的距离:设两直线的方程
{
l
1
:
A
x
+
B
y
+
C
1
=
0
l
2
:
A
x
+
B
y
+
C
2
=
0
\begin{cases} l_1: Ax+By+C_1= 0 \\ l_2: Ax+By+C_2= 0 \end{cases}
{l1:Ax+By+C1=0l2:Ax+By+C2=0,则
d
l
1
,
l
2
=
∣
C
1
−
C
2
∣
A
2
+
B
2
d_{l_1,l_2} = \cfrac{|C_1 - C_2|}{\sqrt{A^2+B^2}}
dl1,l2=A2+B2∣C1−C2∣
-
圆
(1)圆的标准方程:设圆心为 ( a , b ) (a,b) (a,b),半径为 r r r,则方程为 ( x − a ) 2 + ( y − b ) 2 = r 2 (x-a)^2+(y-b)^2=r^2 (x−a)2+(y−b)2=r2
(2)圆的参数方程:圆心在原点的圆方程 x 2 + y 2 = 0 x^2+y^2=0 x2+y2=0,参数方程可以表示为: { x = r cos θ y = r sin θ \begin{cases} x=r\cos\theta\\y=r\sin\theta \end{cases} {x=rcosθy=rsinθ
(3)点与圆的位置关系:点 P ( x 0 , y 0 ) P(x_0,y_0) P(x0,y0)与圆 ( x − a ) 2 + ( y − b ) 2 = r 2 (x-a)^2+(y-b)^2=r^2 (x−a)2+(y−b)2=r2的位置关系,即点 p p p到圆心的距离: d = ( x 0 − a ) 2 + ( y 0 − b ) 2 d=\sqrt{(x_0-a)^2+(y_0-b)^2} d=(x0−a)2+(y0−b)2
(4)直线与圆的位置关系:直线 A x + B y + C = 0 Ax+By+C=0 Ax+By+C=0与圆 ( x − a ) 2 + ( y − b ) 2 = r 2 (x-a)^2+(y-b)^2=r^2 (x−a)2+(y−b)2=r2的位置关系,即圆心的到直线的距离: d = ∣ A a + B b + C ∣ A 2 + B 2 d=\cfrac{|Aa+Bb+C|}{\sqrt{A^2+B^2}} d=A2+B2∣Aa+Bb+C∣ -
空间向量
(1)向量的长度及两点间的距离公式
设 a ( a 1 , a 2 , a 3 ) a(a_1,a_2,a_3) a(a1,a2,a3),则有 ∣ a ∣ = a 1 2 + a 2 2 + a 3 2 |\bm a| = \sqrt{a_1{^2}+a_2{^2}+a_3{^2}} ∣a∣=a12+a22+a32
设 A ( x 1 , y 1 , z 1 ) , B ( x 2 , y 2 , z 2 ) A(x_1,y_1,z_1),B(x_2,y_2,z_2) A(x1,y1,z1),B(x2,y2,z2),则有 d A B = A B → = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + ( z 2 − z 1 ) 2 d_{AB} = \overrightarrow{AB} = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2} dAB=AB=(x2−x1)2+(y2−y1)2+(z2−z1)2
(2)向量数量积的运算:
已知 a = ( a 1 , a 2 , a 3 ) , b = ( b 1 , b 2 , b 3 ) a = (a_1,a_2,a_3),b=(b_1,b_2,b_3) a=(a1,a2,a3),b=(b1,b2,b3)
性质:
a ⊥ b ⟺ a 1 b 1 + a 2 b 2 + a 3 b 3 = 0 a \bot b \iff a_1b_1+a_2b_2+a_3b_3 = 0 a⊥b⟺a1b1+a2b2+a3b3=0
a ∥ b ⟺ a 1 b 1 = a 2 b 2 = a 3 b 3 a \parallel b \iff \cfrac{a_1}{b_1} =\cfrac{a_2}{b_2}=\cfrac{a_3}{b_3} a∥b⟺b1a1=b2a2=b3a3
(3)点到平面的距离:点 P ( x 0 , y 0 , z 0 ) P(x_0,y_0,z_0) P(x0,y0,z0),平面方程 A x + B y + C z + D = 0 Ax+By+Cz+D=0 Ax+By+Cz+D=0,则 d = ∣ A x 0 + B y 0 + C z 0 + D ∣ A 2 + B 2 + C 2 d = \cfrac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}} d=A2+B2+C2∣Ax0+By0+Cz0+D∣ -
其他
圆锥,三角体的体积公式: V = 1 3 S h V=\cfrac{1}{3}Sh V=31Sh(S是底面积,h是高)
弧长公式: l = r θ l=r\theta l=rθ(r是半径, θ \theta θ是圆心角)
椭圆面积公式: S = π a b S=πab S=πab
球体的体积公式: V = 4 π r 3 3 V=\cfrac{4\pi r^3}{3} V=34πr3
球的表面积公式为: S = 4 π r 2 S = 4πr² S=4πr2
二.高数基础
-
两个重要极限(引申)
lim x → 0 sin x x = 1 \lim\limits_{x\to 0}\cfrac{\sin x}{x}=1 x→0limxsinx=1
lim n → ∞ ( 1 + 1 n ) n = e \lim\limits_{n\to \infty}(1+\cfrac{1}{n})^n=e n→∞lim(1+n1)n=e -
无穷小量的比较 (趋近于0的速度)( 高阶,同阶,等价)
当 x → 0 x\to 0 x→0时,
1 − cos x ⟺ x 2 2 1-\cos x \iff\cfrac{x^2}{2} 1−cosx⟺2x2
sin x ⟺ x \sin x \iff x sinx⟺x -
矩阵(三阶行列式)
α = { a 1 , a 2 , a 3 } , β = { b 1 , b 2 , b 3 } \alpha=\{a_1,a_2,a_3\}, \beta=\{b_1,b_2,b_3\} α={a1,a2,a3},β={b1,b2,b3}
α × β = ∣ i j k a 1 a 2 a 3 b 1 b 2 b 3 ∣ = ∣ a 2 a 3 b 2 b 3 ∣ i − ∣ a 1 a 3 b 1 b 3 ∣ j + ∣ a 1 a 2 b 1 b 2 ∣ k \alpha \times \beta =\begin{vmatrix}i & j & k \\a_1 & a_2 & a_3 \\b_1 & b_2 & b_3 \end{vmatrix}= \begin{vmatrix}a_2 & a_3 \\b_2 & b_3\end{vmatrix} i - \begin{vmatrix}a_1 & a_3 \\b_1 & b_3\end{vmatrix}j+ \begin{vmatrix}a_1 & a_2 \\b_1 & b_2\end{vmatrix}k α×β= ia1b1ja2b2ka3b3 = a2b2a3b3 i− a1b1a3b3 j+ a1b1a2b2 k= ( a 2 b 3 − a 3 b 2 ) i − ( a 1 b 3 − a 3 b 1 ) j + ( a 1 b 2 − a 2 b 1 ) k (a_2b_3-a_3b_2)i-(a_1b_3-a_3b_1)j+(a_1b_2-a_2b_1)k (a2b3−a3b2)i−(a1b3−a3b1)j+(a1b2−a2b1)k= { a 2 b 3 − a 3 b 2 , − ( a 1 b 3 − a 3 b 1 ) , a 1 b 2 − a 2 b 1 } \{a_2b_3-a_3b_2,-(a_1b_3-a_3b_1),a_1b_2-a_2b_1\} {a2b3−a3b2,−(a1b3−a3b1),a1b2−a2b1} -
基本初等函数的求导公式:
指数函数: ( e x ) ′ = e x (e^x)' = e^x (ex)′=ex, ( a x ) ′ = a x ln a (a^x)' = a^x\ln a (ax)′=axlna
对数函数: ( ln x ) ′ = 1 x (\ln x)' = \cfrac{1}{x} (lnx)′=x1, ( l o g a x ) ′ = 1 x ln a (log_ax)' =\cfrac{1}{x\ln a} (logax)′=xlna1
正余切函数: ( tan x ) ′ = 1 cos 2 x = sec 2 x (\tan x)' = \cfrac{1}{\cos^2 x} = \sec^2x (tanx)′=cos2x1=sec2x , ( cot x ) ′ = − 1 sin 2 x = − csc 2 x (\cot x)' = -\cfrac{1}{\sin^2 x} = -\csc^2x (cotx)′=−sin2x1=−csc2x
反正余弦函数: ( arcsin x ) ′ = 1 1 − x 2 (\arcsin x)' = \cfrac{1}{\sqrt{1-x^2}} (arcsinx)′=1−x21 , ( arccos x ) ′ = − 1 1 − x 2 (\arccos x)' = - \cfrac{1}{\sqrt{1-x^2}} (arccosx)′=−1−x21
反正余切函数: ( arctan x ) ′ = 1 1 + x 2 (\arctan x)' = \cfrac{1}{1+x^2} (arctanx)′=1+x21 , ( a r c c o t x ) ′ = − 1 1 + x 2 (arccot x)' = - \cfrac{1}{1+x^2} (arccotx)′=−1+x21
-
基本微分公式和微分运算法则(原函数求导数)
d C = 0 dC = 0 dC=0( C C C为常数) d ( x n ) = α x n − 1 d x d(x^n) = \alpha x^{n-1}dx d(xn)=αxn−1dx( α \alpha α为实数)
d ( a x ) = a x ln a d x d(a^x) = a^x\ln a dx d(ax)=axlnadx( a > 0 , a ≠ 1 a>0,a \ne 1 a>0,a=1) d ( e x ) = e x d x d(e^x) = e^x dx d(ex)=exdx
d ( log a x ) = 1 x ln a d x d(\log_a x) = \cfrac{1}{x\ln a} dx d(logax)=xlna1dx( a > 0 , a ≠ 1 a>0,a\ne 1 a>0,a=1) d ( ln x ) = 1 x d x d(\ln x) = \cfrac{1}{x} dx d(lnx)=x1dx
d ( sin x ) = cos x d x d(\sin x) = \cos x dx d(sinx)=cosxdx d ( cos x ) = − sin x d x d(\cos x) = -\sin x dx d(cosx)=−sinxdx
d ( tan x ) = sec 2 x d x d(\tan x) = \sec^2x dx d(tanx)=sec2xdx d ( cot x ) = − csc 2 x d x d(\cot x) = -\csc^2 x dx d(cotx)=−csc2xdx
d ( sec x ) = sec x tan x d x d(\sec x) = \sec x\tan xdx d(secx)=secxtanxdx d ( csc x ) = − csc x cot x d x d(\csc x) = -\csc x\cot xdx d(cscx)=−cscxcotxdx
d ( arcsin x ) = 1 1 − x 2 d x d(\arcsin x) = \cfrac{1}{\sqrt{1-x^2}}dx d(arcsinx)=1−x21dx d ( arccos x ) = − 1 1 − x 2 d x d(\arccos x) = -\cfrac{1}{\sqrt{1-x^2}}dx d(arccosx)=−1−x21dx
d ( arctan x ) = 1 1 + x 2 d x d(\arctan x) = \cfrac{1}{1+x^2}dx d(arctanx)=1+x21dx d ( a r c c o t x ) = − 1 1 + x 2 d x d(arccot x) = -\cfrac{1}{1+x^2}dx d(arccotx)=−1+x21dx
三.高数
第一章 空间解析几何与向量代数
2.向量代数
2.1 向量的方向余弦
α ⃗ = { a 1 , a 2 , a 3 } \vec \alpha = \{a_1,a_2,a_3\} α={a1,a2,a3}
(1) cos 2 α + cos 2 β + cos 2 γ = 1 \cos^2 \alpha+\cos^2 \beta+\cos^2 \gamma=1 cos2α+cos2β+cos2γ=1( α , β , γ 为向量 α ⃗ 的方向角 \alpha,\beta,\gamma为向量\vec \alpha的方向角 α,β,γ为向量α的方向角)
(2) α 0 = α ∣ α ∣ = { a 1 a 1 2 + a 2 2 + a 3 2 , a 2 a 1 2 + a 2 2 + a 3 2 , a 3 a 1 2 + a 2 2 + a 3 2 } \alpha^0 = \cfrac{\alpha}{|\alpha|} = {\{\cfrac{a_1}{\sqrt{a_1{^2}+a_2{^2}+a_3{^2}}},\cfrac{a_2}{\sqrt{a_1{^2}+a_2{^2}+a_3{^2}}},\cfrac{a_3}{\sqrt{a_1{^2}+a_2{^2}+a_3{^2}}}}\} α0=∣α∣α={a12+a22+a32a1,a12+a22+a32a2,a12+a22+a32a3}
6.二次曲面
椭球面: x 2 a 2 + x 2 b 2 + x 2 c 2 = 1 \cfrac{x^2}{a^2}+ \cfrac{x^2}{b^2}+\cfrac{x^2}{c^2}=1 a2x2+b2x2+c2x2=1
椭球抛物面: z = x 2 a 2 + x 2 b 2 z=\cfrac{x^2}{a^2}+ \cfrac{x^2}{b^2} z=a2x2+b2x2
椭圆锥面: z 2 = x 2 a 2 + x 2 b 2 z^2=\cfrac{x^2}{a^2}+ \cfrac{x^2}{b^2} z2=a2x2+b2x2
单页双曲面: x 2 a 2 + x 2 b 2 − x 2 c 2 = 1 \cfrac{x^2}{a^2}+ \cfrac{x^2}{b^2}-\cfrac{x^2}{c^2}=1 a2x2+b2x2−c2x2=1
双叶双曲面: x 2 a 2 + x 2 b 2 − x 2 c 2 = − 1 \cfrac{x^2}{a^2}+ \cfrac{x^2}{b^2}-\cfrac{x^2}{c^2}=-1 a2x2+b2x2−c2x2=−1
第二章 多元函数的微分学
第三章 重积分
一、二重积分
直角坐标下二重积分的计算
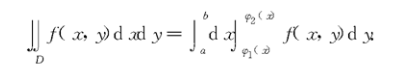
极坐标下二重积分的计算
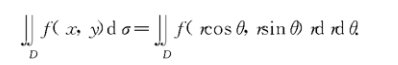
二、 三重积分
直角坐标下三重积分的计算
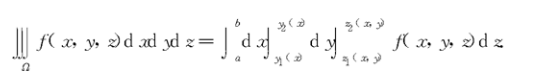
柱面坐标下三重积分的计算
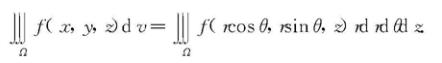
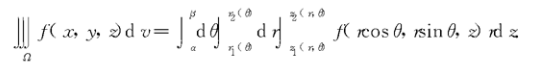
球面坐标下三重积分的计算
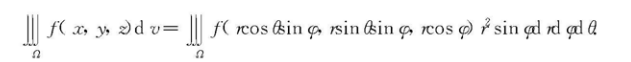
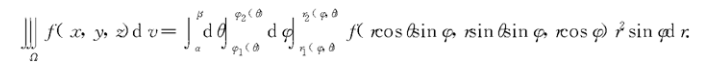
曲面面积
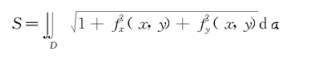
第四章 曲线积分与曲面积分
1、对弧长的曲线积分
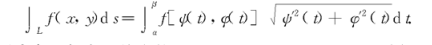
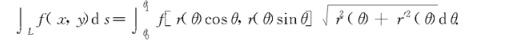
2、对坐标的曲线积分
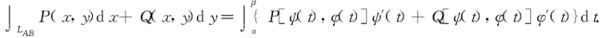
3、格林公式
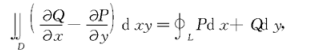
4、对面积的曲线积分
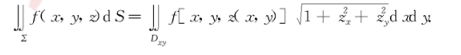
5、对坐标的曲线积分
高斯公式
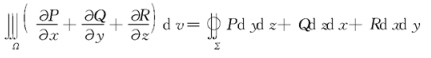
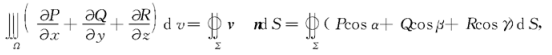
散度
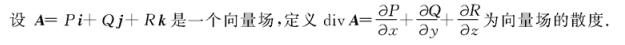
第六章 无穷级数
一、数项级数的审敛法
1、常数项级数
-
性质2: ∑ n = 1 ∞ u n \displaystyle\sum_{n=1}^\infty u_n n=1∑∞un和 ∑ n = 1 ∞ v n \displaystyle\sum_{n=1}^\infty v_n n=1∑∞vn分别收敛与 S S S和 σ \sigma σ, ∑ n = 1 ∞ u n ± v n \displaystyle\sum_{n=1}^\infty u_n\pm v_n n=1∑∞un±vn也收敛于 S ± σ S\pm\sigma S±σ
(1)两个收敛的级数相加(减)后仍收敛
(2)相加(减)后收敛的两个级数未必收敛
收敛+收敛=收敛
收敛+发散=发散
发散+发散=发散或收敛 -
性质4: ∑ u n \displaystyle\sum u_n ∑un收敛,任意加括号的级数也收敛且和不变
(1)加括号后收敛,级数未必收敛
(2)加括号后发散,级数必发散 -
性质5: ∑ u n \displaystyle\sum u_n ∑un收敛,则 lim n → ∞ u n = 0 \displaystyle\lim_{n \rightarrow \infty}u_n = 0 n→∞limun=0
(1) u n → 0 u_n\rightarrow0 un→0 级数未必收敛
(2) u n 不趋近 0 u_n 不趋近0 un不趋近0 级数必发散 -
几何(等比)级数: ∑ n = 1 ∞ a q n − 1 \displaystyle\sum_{n=1}^\infty aq^{n-1} n=1∑∞aqn−1, ∣ q ∣ < 1 |q|<1 ∣q∣<1收敛 S n = a 1 − q S_n = \cfrac{a}{1-q} Sn=1−qa
-
调和级数: ∑ n = 1 ∞ 1 n \displaystyle\sum_{n=1}^\infty \cfrac{1}{n} n=1∑∞n1 发散
2、正项级数
(注意:以下只符合正项级数)
-
∑ u n \displaystyle\sum u_n ∑un和 ∑ v n \displaystyle\sum v_n ∑vn是正项级数,且 u n < v n u_n<v_n un<vn
若 ∑ v n \displaystyle\sum v_n ∑vn收敛,则 ∑ u n \displaystyle\sum u_n ∑un收敛;
若 ∑ u n \displaystyle\sum u_n ∑un发散,则 ∑ v n \displaystyle\sum v_n ∑vn发散 -
p级数: ∑ n = 1 ∞ 1 n p \displaystyle\sum_{n=1}^\infty \cfrac{1}{n^p} n=1∑∞np1 , p > 1 p>1 p>1 收敛
-
比较审敛法:
lim n → ∞ u n v n = l \displaystyle\lim_{n\rightarrow \infty} \cfrac{u_n}{v_n} =l n→∞limvnun=l,当 0 < l < + ∞ 0 < l< +\infty 0<l<+∞时 , u n , v n u_n,v_n un,vn同敛散 -
比值审敛法:
lim n → ∞ u n + 1 u n = ρ \displaystyle\lim_{n\rightarrow \infty} \cfrac{u_{n+1}}{u_n} = \rho n→∞limunun+1=ρ
ρ < 1 \rho < 1 ρ<1收敛, ρ > 1 \rho > 1 ρ>1发散, ρ = 1 \rho = 1 ρ=1 无法比较 -
根植审敛法(柯西判别法):
lim n → ∞ u n n = ρ \displaystyle\lim_{n\rightarrow \infty} \sqrt[n]{u_n} = \rho n→∞limnun=ρ
ρ < 1 \rho < 1 ρ<1收敛, ρ > 1 \rho > 1 ρ>1发散, ρ = 1 \rho = 1 ρ=1 无法比较
3、交错级数
莱布尼兹审敛法:
∑ n = 1 + ∞ ( − 1 ) n − 1 u n = ρ \displaystyle\sum_{n =1}^ {+\infty} (-1)^{n-1}u_n = \rho n=1∑+∞(−1)n−1un=ρ ( u n ≥ 0 ) (u_n\ge 0) (un≥0)
(1) u n ≥ u n + 1 u_n \ge u_{n+1} un≥un+1
(2) lim n → ∞ u n = 0 \displaystyle\lim_{n\rightarrow \infty}u_n = 0 n→∞limun=0 ,则级数收敛, S ≤ u 1 , ∣ r n ∣ ≤ u n + 1 S \le u_1,|r_n| \le u_{n+1} S≤u1,∣rn∣≤un+1
4、任意项级数
-
∑
n
=
1
+
∞
u
n
=
u
1
+
u
2
+
u
3
+
…
…
\displaystyle\sum_{n =1}^ {+\infty} u_n=u_1+u_2+u_3+……
n=1∑+∞un=u1+u2+u3+……是任意项级数
lim n → ∞ u n + 1 u n = l \displaystyle\lim_{n\rightarrow \infty} \cfrac{u_{n+1}}{u_n} = l n→∞limunun+1=l (正项的比值审敛法)
l < 1 l < 1 l<1时, ∑ u n \displaystyle\sum u_n ∑un收敛,
l > 1 l > 1 l>1时, ∑ u n \displaystyle\sum u_n ∑un发散
l = 1 l= 1 l=1 无法比较
二、幂级数
-
定理1 (阿贝尔定理)
∑ n = 0 + ∞ a n x n \displaystyle\sum_{n =0}^ {+\infty} a_nx^n n=0∑+∞anxn
x = x 0 x=x_0 x=x0时收敛, ∣ x ∣ < x 0 |x|<x_0 ∣x∣<x0,幂级数绝对收敛
x = x 0 x=x_0 x=x0时发散, ∣ x ∣ > x 0 |x|>x_0 ∣x∣>x0,幂级数发散
推论:
(1) x = 0 x=0 x=0 收敛
(2) x ∈ ( − ∞ , + ∞ ) x \in (-\infty,+\infty) x∈(−∞,+∞) 收敛
(3) ∣ x ∣ < R |x| <R ∣x∣<R 绝对收敛 -
定理2: lim n → ∞ ∣ a n + 1 a n ∣ = ρ \displaystyle\lim_{n \rightarrow \infty} |\cfrac{a_{n+1}}{a_n}| = \rho n→∞lim∣anan+1∣=ρ , R = 1 ρ = { R = + ∞ , ( ρ = 0 ) R = 0 , ( ρ = + ∞ ) R = 1 ρ , ( ρ ≠ 0 ) R = \cfrac{1}{\rho} =\begin{cases} R=+\infty,(\rho=0)\\R=0,(\rho=+\infty) \\R= \cfrac{1}{\rho},(\rho\ne0)\end{cases} R=ρ1=⎩ ⎨ ⎧R=+∞,(ρ=0)R=0,(ρ=+∞)R=ρ1,(ρ=0)
-
性质1: ∑ n = 0 + ∞ a n x n \displaystyle\sum_{n =0}^ {+\infty} a_nx^n n=0∑+∞anxn 的和函数 S ( x ) S(x) S(x)在收敛域 I I I是连续的
性质2: ∑ n = 0 + ∞ a n x n \displaystyle\sum_{n =0}^ {+\infty} a_nx^n n=0∑+∞anxn 的和函数 S ( x ) S(x) S(x)在收敛域 I I I可积
∫ 0 x S ( t ) d t = ∫ 0 x ( ∑ n = 0 ∞ a n t n ) d t = ∑ n = 0 + ∞ ∫ 0 x a n t n d t = ∑ n = 0 + ∞ a n n + 1 x n + 1 d t ( x ∈ I ) \int_0^x S(t)dt=\int_0^x(\displaystyle\sum_{n =0}^ {\infty} a_nt^n)dt = \displaystyle\sum_{n =0}^ {+\infty} \int_0^xa_nt^ndt =\displaystyle\sum_{n =0}^ {+\infty} \cfrac{a_n}{n+1}x^{n+1}dt (x \in I) ∫0xS(t)dt=∫0x(n=0∑∞antn)dt=n=0∑+∞∫0xantndt=n=0∑+∞n+1anxn+1dt(x∈I)
逐项求积分后与原幂级数的收敛半径相同,重新考查端点处,得出新的幂级数的收敛域性质3: S ( x ) S(x) S(x)在 ( − R , R ) (-R,R) (−R,R)可导
S ( x ) ′ = ( ∑ n = 0 ∞ a n x n ) ′ = ∑ n = 0 ∞ ( a n x n ) ′ = ∑ n = 0 ∞ n a n x n − 1 S(x)'=(\displaystyle\sum_{n =0}^ {\infty} a_{n}x^n)'=\displaystyle\sum_{n=0}^{\infty}(a_nx^n)'=\displaystyle\sum_{n=0}^{\infty}na_nx^{n-1} S(x)′=(n=0∑∞anxn)′=n=0∑∞(anxn)′=n=0∑∞nanxn−1
三、函数的幂级数展开式
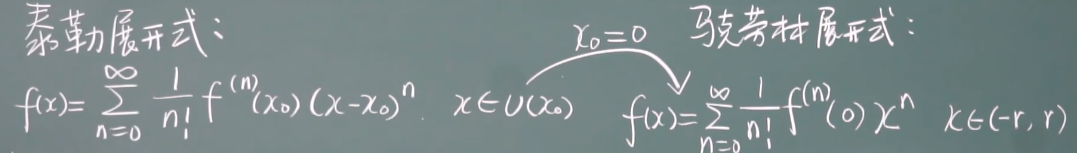

e
x
=
∑
n
=
0
∞
x
n
n
!
,
(
−
∞
<
x
<
+
∞
)
e^x = \displaystyle\sum_{n =0}^ {\infty} \cfrac{x^n}{n!},(-\infty<x<+\infty)
ex=n=0∑∞n!xn,(−∞<x<+∞)
sin x = ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 2 n + 1 , ( − ∞ < x < + ∞ ) \sin x = \displaystyle\sum_{n =0}^ {\infty} \cfrac{(-1)^{n}x^{2n+1}}{2n+1},(-\infty<x<+\infty) sinx=n=0∑∞2n+1(−1)nx2n+1,(−∞<x<+∞)
1 1 − x = ∑ n = 0 ∞ x n , ( − 1 < x < 1 ) \cfrac{1}{1-x} = \displaystyle\sum_{n =0}^ {\infty} x^n,(-1<x<1) 1−x1=n=0∑∞xn,(−1<x<1)
四、傅里叶幂级数
欧拉-傅里叶级数: f ( x ) = a 0 2 + ∑ n = 1 ∞ ( a n cos n x + b n sin n x ) f(x) =\cfrac{a_0}{2}+\displaystyle\sum_{n =1}^ {\infty} (a_n\cos nx+b_n\sin nx) f(x)=2a0+n=1∑∞(ancosnx+bnsinnx)
欧拉-傅里叶公式:
a 0 = 1 π ∫ − π π f ( x ) d x a_0=\cfrac{1}{\pi} \int_{-\pi}^ {\pi}f(x)dx a0=π1∫−ππf(x)dx
a n = 1 π ∫ − π π f ( x ) cos n x d x a_n=\cfrac{1}{\pi} \int_{-\pi}^ {\pi} f(x) \cos nx dx an=π1∫−ππf(x)cosnxdx ( n = 1 , 2 , … (n = 1,2,… (n=1,2,…)
b n = 1 π ∫ − π π f ( x ) sin n x d x b_n=\cfrac{1}{\pi} \int_{-\pi}^ {\pi} f(x) \sin nx dx bn=π1∫−ππf(x)sinnxdx ( n = 1 , 2 , … (n = 1,2,… (n=1,2,…)