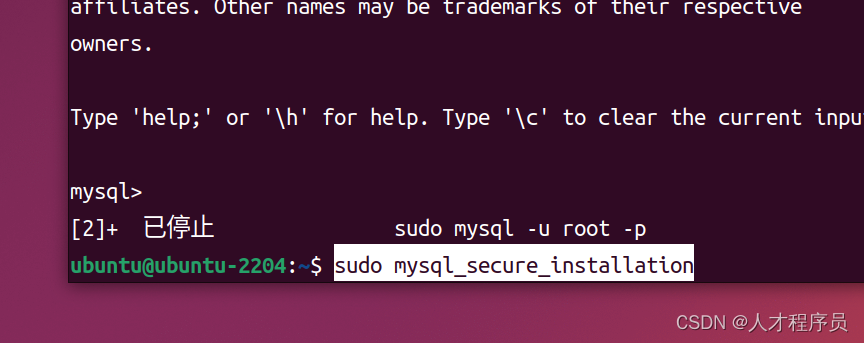
文章目录
- 背景
- 递归树法
- 案例一
- 案例二
- 局限性
- 代入法/替代法
- 主方法(重点)
背景
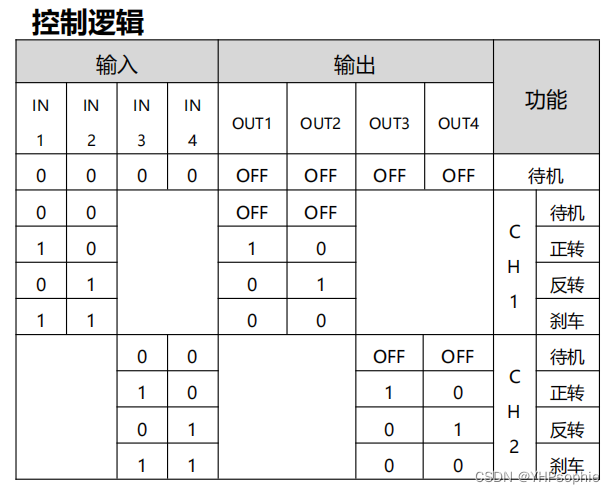
当碰到形如 T ( n ) = a T ( ⌈ n b ⌉ ) + O ( n d ) T(n)=aT(\lceil \frac{n}{b} \rceil)+O(n^d) T(n)=aT(⌈bn⌉)+O(nd)的递推式,本质上就是将问题转化为规模更小的子问题求解,此时有三种思路。
递归树法
案例一
T
(
n
)
=
{
2
T
(
n
2
)
+
n
i
f
n
>
1
1
i
f
n
=
1
T(n)=\left\{ \begin{array}{ll} 2T(\frac{n}{2})+n & if \space n>1 \\ 1 & if \space n=1 \nonumber \end{array} \right.
T(n)={2T(2n)+n1if n>1if n=1
可以利用递归树:
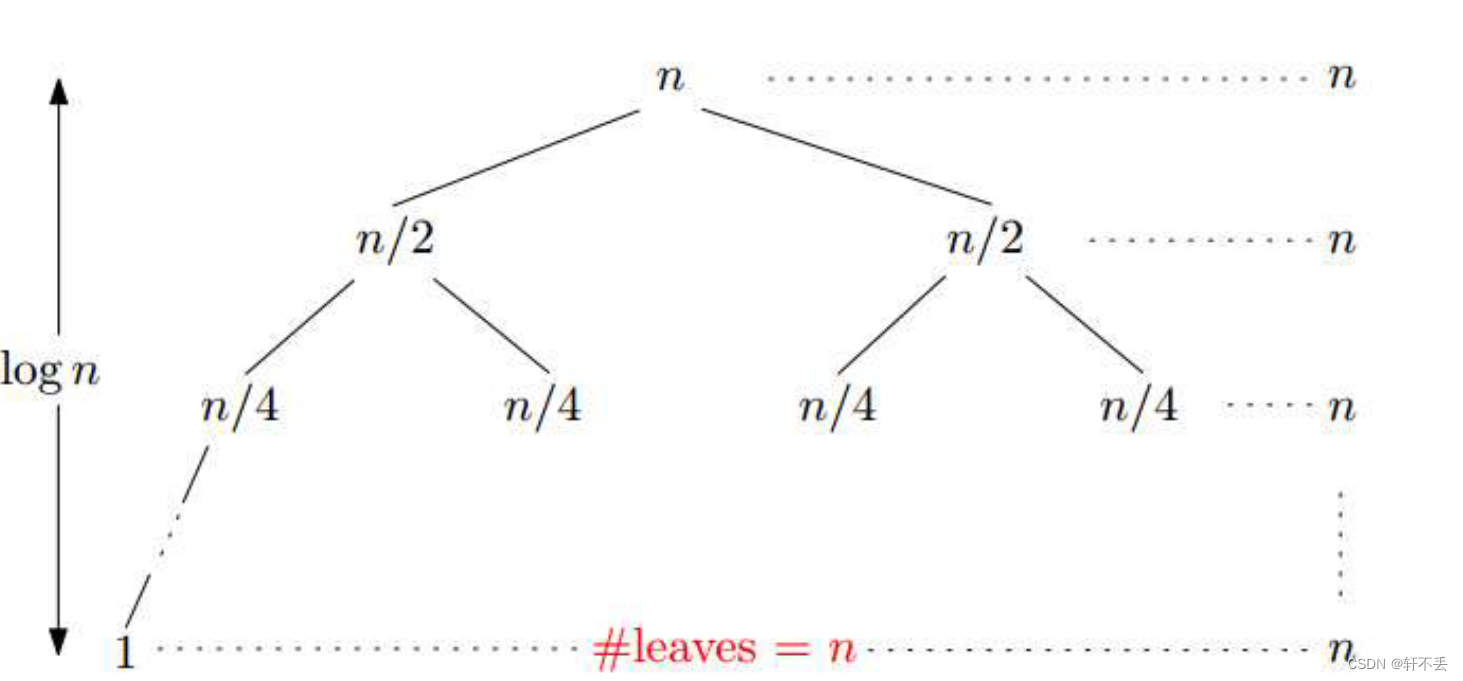
画出树,高满足
2
h
=
n
2^h=n
2h=n,因此
h
=
l
o
g
2
n
h=log_{2}n
h=log2n,而叶子共有n个,因此总的时间复杂度
T
(
n
)
=
n
l
o
g
n
T(n)=nlogn
T(n)=nlogn
案例二
T
(
n
)
=
{
3
T
(
n
4
)
+
n
2
i
f
n
>
1
1
i
f
n
=
1
T(n)=\left\{ \begin{array}{ll} 3T(\frac{n}{4})+n^2 & if \space n>1 \\ 1 & if \space n=1 \nonumber \end{array} \right.
T(n)={3T(4n)+n21if n>1if n=1

每层个数即
3
h
3^h
3h个。最后一层高度
h
=
l
o
g
4
n
h=log_4n
h=log4n,再利用对数技巧代入,即可求出叶子的个数,而时间复杂度为:
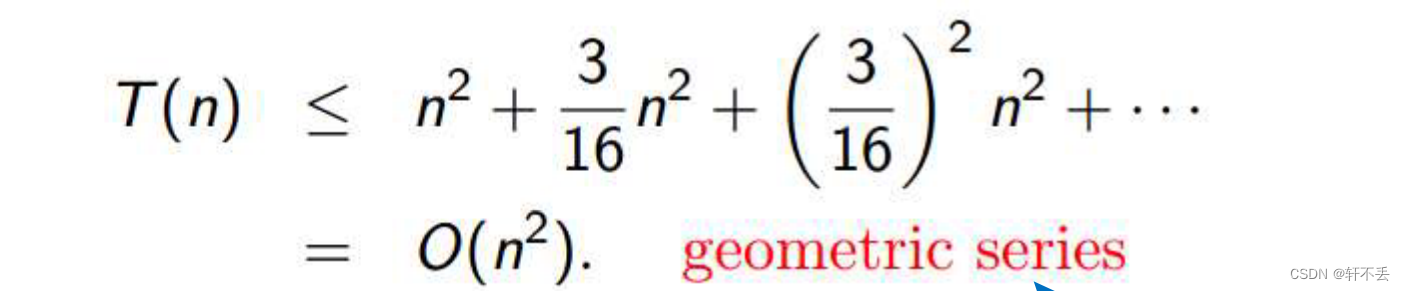
等比数列求解
局限性
T
(
n
)
=
{
T
(
n
3
)
+
T
(
2
n
3
)
+
n
i
f
n
>
2
1
i
f
n
=
1
,
2
T(n)=\left\{ \begin{array}{ll} T(\frac{n}{3})+ T(\frac{2n}{3})+n & if \space n>2 \\ 1 & if \space n=1,2 \nonumber \end{array} \right.
T(n)={T(3n)+T(32n)+n1if n>2if n=1,2
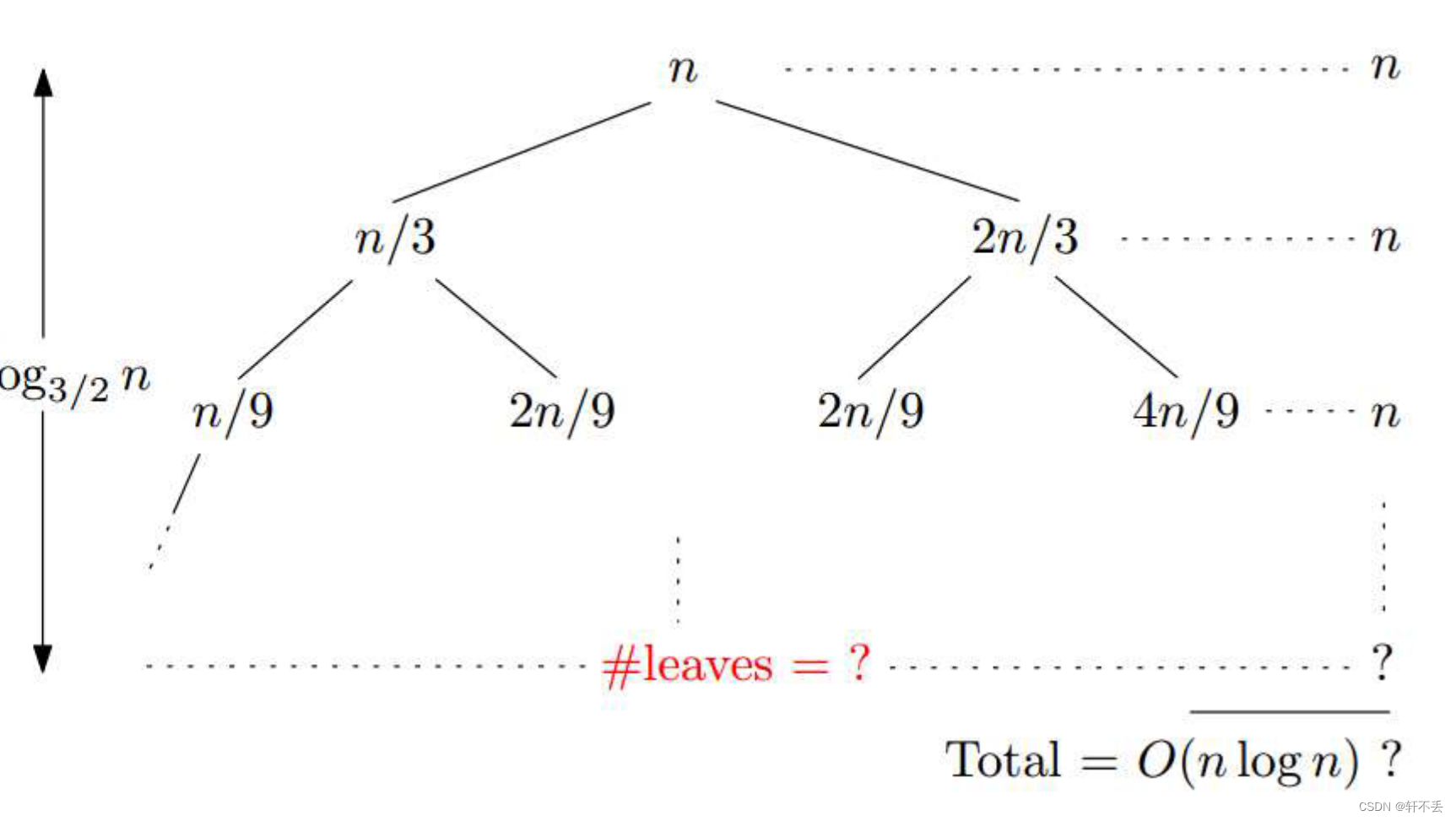
此时树的高度不一致,无法计算
代入法/替代法
此法先假设时间复杂度,再去验证假设成立。因此最难之处在于怎么假设,用处不大
主方法(重点)
T ( n ) = a T ( ⌈ n b ⌉ ) + O ( n d ) T(n)=aT(\lceil \frac{n}{b} \rceil)+O(n^d) T(n)=aT(⌈bn⌉)+O(nd)的时间复杂度如下:
T ( n ) = { O ( n d ) d > log b a O ( n d l o g n ) d = log b a O ( n log b a ) d < log b a T(n)=\left\{ \begin{array}{ll} O(n^d) & d>\log_{b}a \\\\ O(n^{d}logn) & d=\log_{b}a \\\\ O(n^{\log_{b}a}) & d<\log_{b}a \nonumber \end{array} \right. T(n)=⎩ ⎨ ⎧O(nd)O(ndlogn)O(nlogba)d>logbad=logbad<logba
以后碰到这种递推分治式子代入公式即可