文章目录
- 考点
- 记忆/考点汇总——按大纲
- 整体
- 目录大纲法
- 记忆宫殿法
- 绘图记忆法
- 局部
- 数字编码法
- 归类记忆法
- 重点记忆法
- 歌决记忆法
- 谐音记忆法
- 理解记忆法
- 比较记忆法
- 转图像记忆法
- 可视化法
本篇思路:根据各方的资料,比如名师的资料,按大纲或者其他方式,收集/汇总考点,即需记忆点,在通过整体的记忆法,比如整体信息很多,通常使用记忆宫殿法,绘图记忆法进行记忆,针对局部/细节/组成的部分,可通过多种方法,比如联想记忆法、理解记忆法等进行进一步记忆。
考点
通过汇总各方大佬资料,作为收集考点/记忆点的信息输入:XX,收集汇总如下:
汇总考点的必要,或者说,汇总记忆的内容的必要,不言而喻,首先,你要记忆东西,得有东西,所以你要梳理出你需要记忆的全部东西,其次,在收集多个大佬的梳理的考点,又可以找出各条逻辑帮助记忆考点,所以,梳理考点是很有必要的,是记忆的基础,是记忆宫殿里面的物品,是我们最后考试需要去找到的解题物品。
记忆/考点汇总——按大纲
——整式——
六大公式:
平方差公式:
a
2
−
b
2
=
(
a
+
b
)
(
a
−
b
)
a^2-b^2=(a+b)(a-b)
a2−b2=(a+b)(a−b)——【平方差公式有两项,符号相反切记牢,首加尾乘首减尾,莫与完全公式相混淆。】
完全平方:
(
a
±
b
)
2
=
a
2
±
2
a
b
+
b
2
(a±b)^2=a^2±2ab+b^2
(a±b)2=a2±2ab+b2——【完全平方有三项,首尾符号是同乡,首平方、尾平方,首尾二倍放中央;首±尾括号带平方,尾项符号随中央。】
配方公式:
a
2
+
b
2
+
c
2
±
a
b
±
b
c
±
a
c
=
1
2
[
(
a
±
b
)
2
+
(
a
±
c
)
2
(
b
±
c
)
2
]
a^2+b^2+c^2±ab±bc±ac=\frac{1}{2}[(a±b)^2+(a±c)^2(b±c)^2]
a2+b2+c2±ab±bc±ac=21[(a±b)2+(a±c)2(b±c)2]
立方和公式:
a
3
+
b
3
=
(
a
+
b
)
(
a
2
−
a
b
+
b
2
)
a^3+b^3=(a+b)(a^2-ab+b^2)
a3+b3=(a+b)(a2−ab+b2)
立方差公式:
a
3
−
b
3
=
(
a
−
b
)
(
a
2
+
a
b
+
b
2
)
a^3-b^3=(a-b)(a^2+ab+b^2)
a3−b3=(a−b)(a2+ab+b2)
和与差的立方公式:
a
3
±
b
3
=
(
a
±
b
)
(
a
2
∓
a
b
+
b
2
)
a^3±b^3=(a±b)(a^2∓ab+b^2)
a3±b3=(a±b)(a2∓ab+b2)——【】
拓展:
三个数的完全平方:
(
a
+
b
+
c
)
2
=
a
2
+
b
2
+
c
2
+
2
a
b
+
2
b
c
+
2
a
c
(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ac
(a+b+c)2=a2+b2+c2+2ab+2bc+2ac——【】
整式的除法:若
F
(
x
)
F(x)
F(x)除以
f
(
x
)
f(x)
f(x),商是
g
(
x
)
g(x)
g(x),余式是
r
(
x
)
r(x)
r(x),则有
F
(
x
)
=
f
(
x
)
g
(
x
)
+
r
(
x
)
F(x)=f(x)g(x)+r(x)
F(x)=f(x)g(x)+r(x),并且
r
(
x
)
r(x)
r(x)的次数小于
f
(
x
)
f(x)
f(x)的次数。
当
r
(
x
)
=
0
r(x)=0
r(x)=0时,
F
(
x
)
=
f
(
x
)
g
(
x
)
F(x)=f(x)g(x)
F(x)=f(x)g(x),此时称
F
(
x
)
F(x)
F(x)能被
f
(
x
)
f(x)
f(x)整除(也能被
g
(
x
)
g(x)
g(x)整除,
f
(
x
)
f(x)
f(x)和
g
(
x
)
g(x)
g(x)都是
F
(
x
)
F(x)
F(x)的因式)。
因式定理(整除):
f
(
x
)
f(x)
f(x)含有
(
x
−
a
)
(x-a)
(x−a)因式
⟺
⟺
⟺
f
(
x
)
f(x)
f(x)能被
(
x
−
a
)
(x-a)
(x−a)整除
⟺
⟺
⟺
f
(
a
)
=
0
f(a)=0
f(a)=0——【理解记忆法:f(x)能被ax-b整除,意味着f(x)含有ax-b因式,即
f
(
b
a
)
=
0
f(\frac{b}{a})=0
f(ab)=0】——【因式定理是余式定理的一种特殊情况,即余式刚好为0】
当
x
=
a
x=a
x=a时,
f
(
a
)
=
0
f(a)=0
f(a)=0
⟺
⟺
⟺
x
−
a
x-a
x−a是
f
(
x
)
f(x)
f(x)的一个因式
⟺
⟺
⟺
f
(
x
)
f(x)
f(x)能被
x
−
a
x-a
x−a整除。
余式定理(非整除):由于余式的次数要小于除式,所以当除式为一次表达式时,余式就为常数,从而得到余式定理:多项式
f
(
x
)
f(x)
f(x)除以
x
−
a
x-a
x−a,余式为
f
(
a
)
,推论为:
f(a),推论为:
f(a),推论为:多项式
f
(
x
)
f(x)
f(x)除以
a
x
−
b
ax-b
ax−b的余式为
f
(
b
a
)
f(\frac{b}{a})
f(ab)。此外,函数
f
(
a
)
f(a)
f(a)的值代表
f
(
x
)
f(x)
f(x)除以
x
−
a
x-a
x−a的余式。
评注:可以理解为
f
(
x
)
f(x)
f(x)除以
a
x
−
b
ax-b
ax−b的余式为该点的函数值。因式定理可以看成余式定理的特殊情况。——【】
(1)若有
x
=
a
x=a
x=a使得
f
(
a
)
=
0
f(a)=0
f(a)=0,则
F
(
a
)
=
r
(
a
)
F(a)=r(a)
F(a)=r(a),即当除式=0时,被除式=余式。
(2)
F
(
x
)
F(x)
F(x)除以
a
x
−
b
ax-b
ax−b,当除式
a
x
−
b
=
0
ax-b=0
ax−b=0时,被除式等于余式,即
F
(
b
a
)
=
余式
F(\frac{b}{a})=余式
F(ab)=余式。
(3)
F
(
x
)
F(x)
F(x)除以
a
x
2
+
b
x
+
c
ax^2+bx+c
ax2+bx+c,可令除式
a
x
2
+
b
x
+
c
=
0
ax^2+bx+c=0
ax2+bx+c=0,解得两个根
x
1
,
x
2
x_1,x_2
x1,x2,则有余式
R
(
x
1
)
=
F
(
x
1
)
R(x_1)=F(x_1)
R(x1)=F(x1),
R
(
x
2
)
=
F
(
x
2
)
R(x_2)=F(x_2)
R(x2)=F(x2)。
二项式定理:
(
a
+
b
)
n
=
C
n
0
a
n
+
C
n
1
a
n
−
1
b
+
.
.
.
+
C
n
k
a
n
−
k
b
k
+
.
.
.
+
C
n
n
−
1
a
b
n
−
1
+
C
n
n
b
n
(a+b)^n=C_n^0a^n+C_n^1a^{n-1}b+...+C_n^ka^{n-k}b^k+...+C_n^{n-1}ab^{n-1}+C_n^nb^n
(a+b)n=Cn0an+Cn1an−1b+...+Cnkan−kbk+...+Cnn−1abn−1+Cnnbn,其中第
k
+
1
k+1
k+1项为
T
k
+
1
=
C
n
k
a
n
−
k
b
k
T_{k+1}=C_n^ka^{n-k}b^k
Tk+1=Cnkan−kbk,称为通项。
——分式——
1.已知
x
+
1
x
=
a
x+\frac{1}{x}=a
x+x1=a或者
x
2
+
a
x
+
1
=
0
x^2+ax+1=0
x2+ax+1=0,求代数式的值
(1)求整式的值
①降次法
1)方程中降次:已知
x
2
+
a
x
+
1
=
0
x^2+ax+1=0
x2+ax+1=0型,可化简,从而实现降次。
例:已知
a
2
−
3
a
+
1
=
0
a^2-3a+1=0
a2−3a+1=0,则有
a
2
=
3
a
−
1
,
a
2
−
3
a
=
−
1
,
a
2
+
1
=
3
a
,
a
+
1
a
=
3
a^2=3a-1,a^2-3a=-1,a^2+1=3a,a+\frac{1}{a}=3
a2=3a−1,a2−3a=−1,a2+1=3a,a+a1=3
2)有理化降次:若已知一个无理数,可将所给无理数凑配成有理数,然后再进行降次。
例:已知
a
=
2
+
1
a=\sqrt{2}+1
a=2+1,则
a
−
2
=
2
−
1
a-2=\sqrt{2}-1
a−2=2−1,根据平方差公式,可得
a
(
a
−
2
)
=
1
a(a-2)=1
a(a−2)=1,则有
a
2
−
2
a
=
1
,
a
2
=
2
a
+
1
,
a
2
−
1
=
2
a
,
a
−
1
a
=
2
a^2-2a=1,a^2=2a+1,a^2-1=2a,a-\frac{1}{a}=2
a2−2a=1,a2=2a+1,a2−1=2a,a−a1=2
②整式的除法
若已知
x
2
+
a
x
+
1
=
0
x^2+ax+1=0
x2+ax+1=0,则可用
f
(
x
)
f(x)
f(x)除以是
x
2
+
a
x
+
1
x^2+ax+1
x2+ax+1,如果所得余式为常数,则此常数为
f
(
x
)
f(x)
f(x)的值。
(2)求分式的值
已知
x
+
1
x
=
a
x+\frac{1}{x}=a
x+x1=a,求形如
x
3
+
1
x
3
x^3+\frac{1}{x^3}
x3+x31,
x
4
+
1
x
4
x^4+\frac{1}{x^4}
x4+x41等分式的值。
解法:将已知条件平方升次,或者将未知分式因式分解降次,即可求解。
例:
x
+
1
x
=
3
x+\frac{1}{x}=3
x+x1=3
⟹
\Longrightarrow
⟹
x
2
+
1
x
2
=
7
x^2+\frac{1}{x^2}=7
x2+x21=7
⟹
\Longrightarrow
⟹
x
3
+
1
x
3
=
18
x^3+\frac{1}{x^3}=18
x3+x31=18
⟹
\Longrightarrow
⟹
x
4
+
1
x
4
=
47
x^4+\frac{1}{x^4}=47
x4+x41=47
⟹
\Longrightarrow
⟹
x
5
+
1
x
5
=
123
x^5+\frac{1}{x^5}=123
x5+x51=123;
x
+
1
x
=
3
x+\frac{1}{x}=3
x+x1=3
⟹
\Longrightarrow
⟹
x
−
1
x
=
±
5
x-\frac{1}{x}=±\sqrt{5}
x−x1=±5;
x
2
+
1
x
2
=
7
x^2+\frac{1}{x^2}=7
x2+x21=7
⟹
\Longrightarrow
⟹
x
+
1
x
=
±
3
x+\frac{1}{x}=±3
x+x1=±3。
2.关于
1
a
+
1
b
+
1
c
=
0
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0
a1+b1+c1=0的问题
定理:若
1
a
+
1
b
+
1
c
=
0
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0
a1+b1+c1=0,则
(
a
+
b
+
c
)
2
=
a
2
+
b
2
+
c
2
(a+b+c)^2=a^2+b^2+c^2
(a+b+c)2=a2+b2+c2
证明:
(
a
+
b
+
c
)
2
=
a
2
+
b
2
+
c
2
+
2
a
b
+
2
a
c
+
2
b
c
(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc
(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,由于
1
a
+
1
b
+
1
c
=
a
b
+
a
c
+
b
c
a
b
c
=
0
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{ab+ac+bc}{abc}=0
a1+b1+c1=abcab+ac+bc=0,故有
a
b
+
a
c
+
b
c
=
0
ab+ac+bc=0
ab+ac+bc=0,所以,
(
a
+
b
+
c
)
2
=
a
2
+
b
2
+
c
2
(a+b+c)^2=a^2+b^2+c^2
(a+b+c)2=a2+b2+c2。
整体
整体使用记忆宫殿法和绘图记忆法等进行记忆
目录大纲法
记忆宫殿法
绘图记忆法
局部
学习记忆——数学篇——汇总——顺口溜记忆法+谐音记忆法+理解记忆法+归类记忆法+重点记忆法+比较记忆法+转图像记忆法
数字编码法
学习记忆——记忆宫殿——编码——数字编码和字母编码——两位数
学习记忆——英语——字母编码
学习记忆——记忆宫殿——编码——数字编码——数字声母
归类记忆法
数学知识有一个最显著的特点,就是系统性很强。数学知识之间有着内在的联系,我们可以按照它们的特性,恰当归类,使之条理化、系统化,组成一个便于记忆的知识网络。
整式运算:
五大核心公式:完全平方式、平方差公式、三个数和的平方、立方和差与和差立方、其他公式
or 六大公式:平方差公式、完全平方公式、三个数的完全平方公式、配方公式、立方和差公式、和差的立方公式
重点记忆法
抓住一个重点,去推导,去联想。
平方差→立方差
a
2
−
b
2
=
(
a
+
b
)
(
a
−
b
)
a^2-b^2=(a+b)(a-b)
a2−b2=(a+b)(a−b)
→
a
3
-
b
3
=
(
a
-
b
)
(
a
2
+
a
b
+
b
2
)
a^3-b^3=(a-b)(a^2+ab+b^2)
a3-b3=(a-b)(a2+ab+b2)
→
a
3
+
b
3
=
(
a
+
b
)
(
a
2
-
a
b
+
b
2
)
a^3+b^3=(a+b)(a^2-ab+b^2)
a3+b3=(a+b)(a2-ab+b2)
完全平方(其实就是和差的平方)→和差的立方【效果感觉差强人意,但是差雀食是符号要特别注意】
(
a
+
b
)
2
=
a
2
+
2
a
b
+
b
2
(a+b)^2=a^2+2ab+b^2
(a+b)2=a2+2ab+b2
→
(
a
+
b
)
3
=
a
3
+
3
a
2
b
+
3
a
b
2
+
b
3
(a+b)^3=a^3+3a^2b+3ab^2+b^3
(a+b)3=a3+3a2b+3ab2+b3
(
a
−
b
)
2
=
a
2
−
2
a
b
+
b
2
(a-b)^2=a^2-2ab+b^2
(a−b)2=a2−2ab+b2
→
(
a
−
b
)
3
=
a
3
−
3
a
2
b
+
3
a
b
2
−
b
3
(a-b)^3=a^3-3a^2b+3ab^2-b^3
(a−b)3=a3−3a2b+3ab2−b3
歌决记忆法
谐音记忆法
理解记忆法
比较记忆法
平方差公式你肯定记得,那就平方差关联上立方差
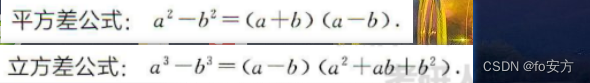
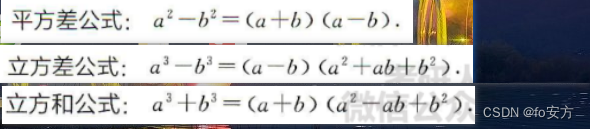
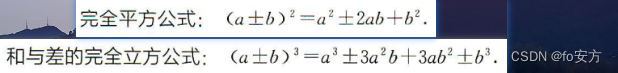
转图像记忆法
学习记忆——数学篇——转图像记忆法
可视化法
管理类联考——数学——可视化篇——代数即几何