汇编语言-div指令溢出问题

8086CPU中被除数保存在ax(16位)或ax和dx（32位）中，如果被除数为16位，进行除法运算时al保存商，ah保存余数。如果被除数为32位时，进行除法运算时，ax保存商，dx保存余数。16位的数据除8位的数据时，最终得到的商可能大于8位，al保存不下会产生除法溢出。可以采用一些其他方法避免除法溢出问题。

例子：898762 ÷ 11拆分运算(注意:[]表示取整)
$$[\frac{898}{11}]\times 1000+\frac{((898\mathrm{mod}11)\times 1000+762)}{11}$$
计算结果：810*1000+705…7

解释：898762使用16位存储不下，只能使用32位进行存储，11可以使用16位存储，他们的计算结果大于16位，会产生除法溢出。上述例子中可以将810存储到一个寄存器，705存储到一个寄存器，然后使用单独的一个寄存器储存余数，就能解决产生溢出的问题。

使用CPU解决该问题：将高位储存到dx中，低位储存到ax中，cx储存余数。

(00000000 00001101 10110110 11001010) ₂ = (898762)₁₀

1.cx存储除数，将被除数存储到栈中。

mov ax,[bx]
push ax
inc bx
mov ax,bx	
mov cx,11
mov dx,0

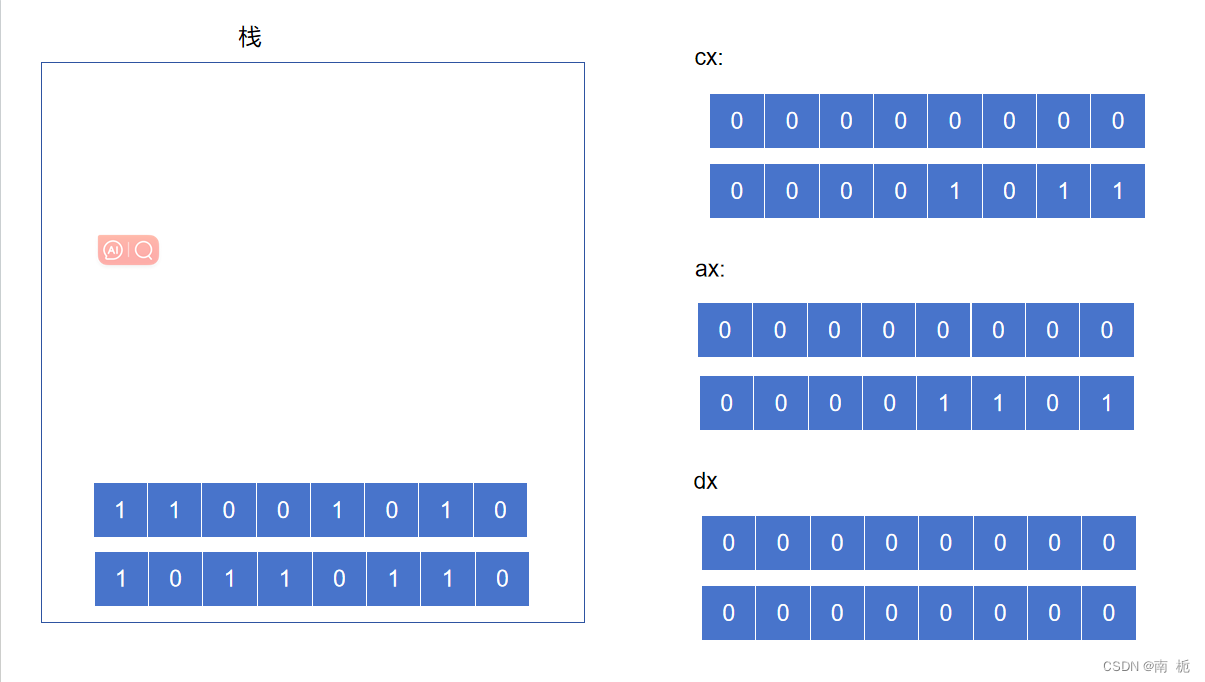
2.计算高位除以除数的结果

div cx

3.将高位结果临时储存至bx，并将低位取出

mov bx,ax
pop ax

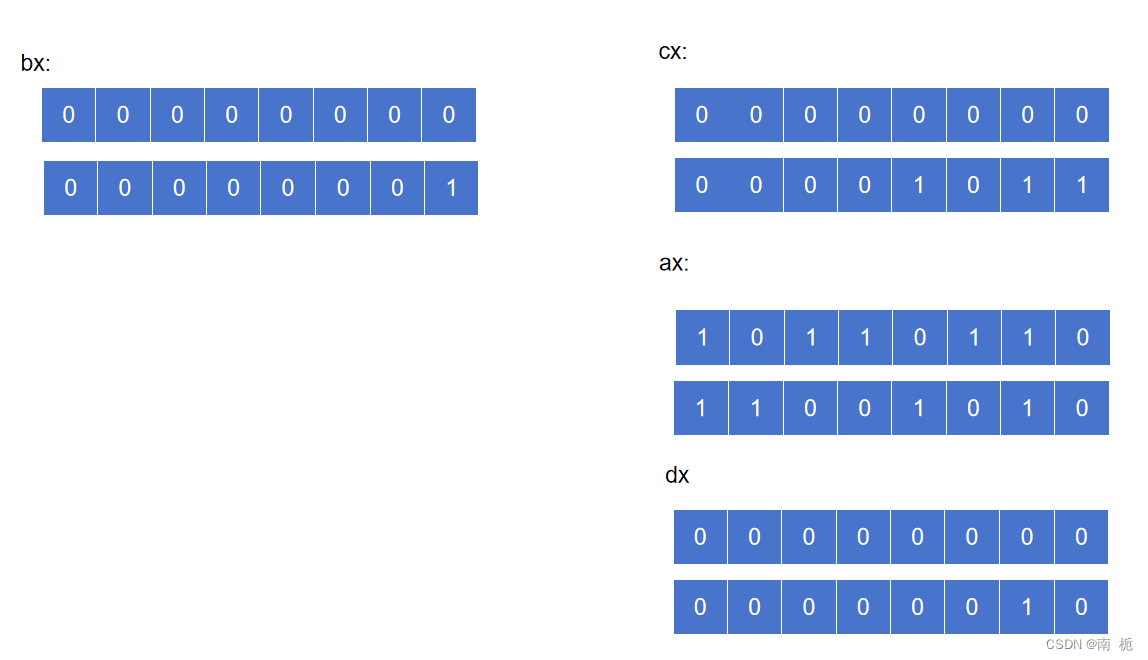
4.再次计算除cx的值，得到余数和商

div cx

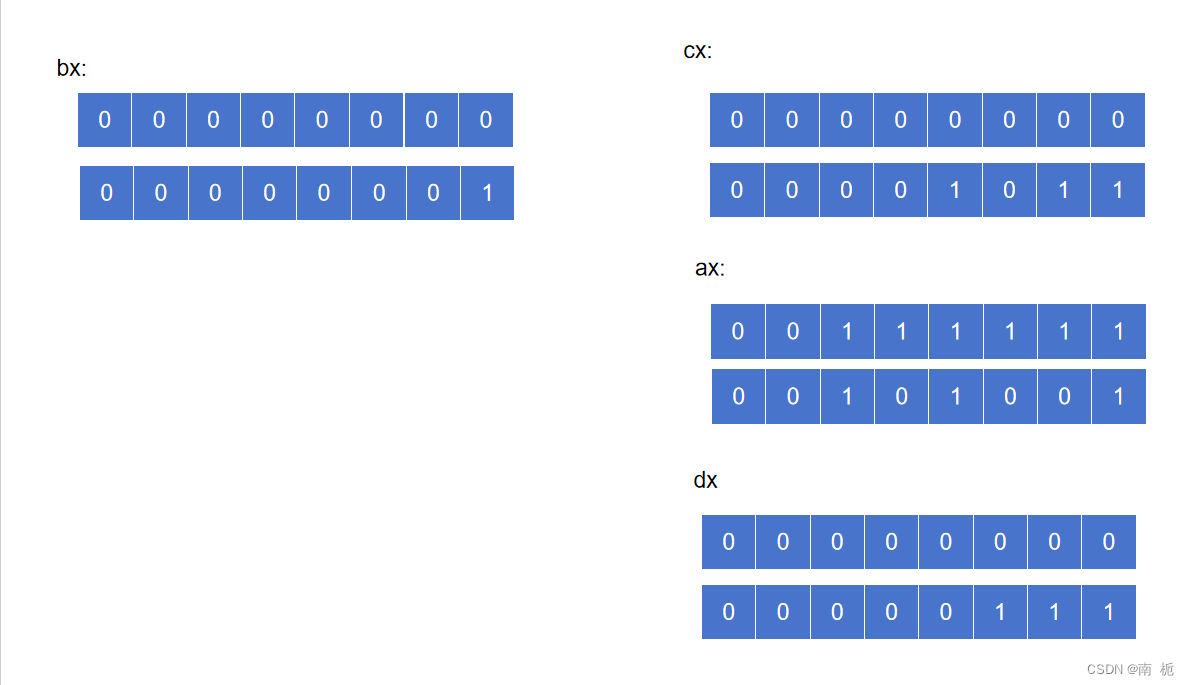
5.将余数保存到cx，将高位保存到dx

mov cx,dx
mov dx,bx

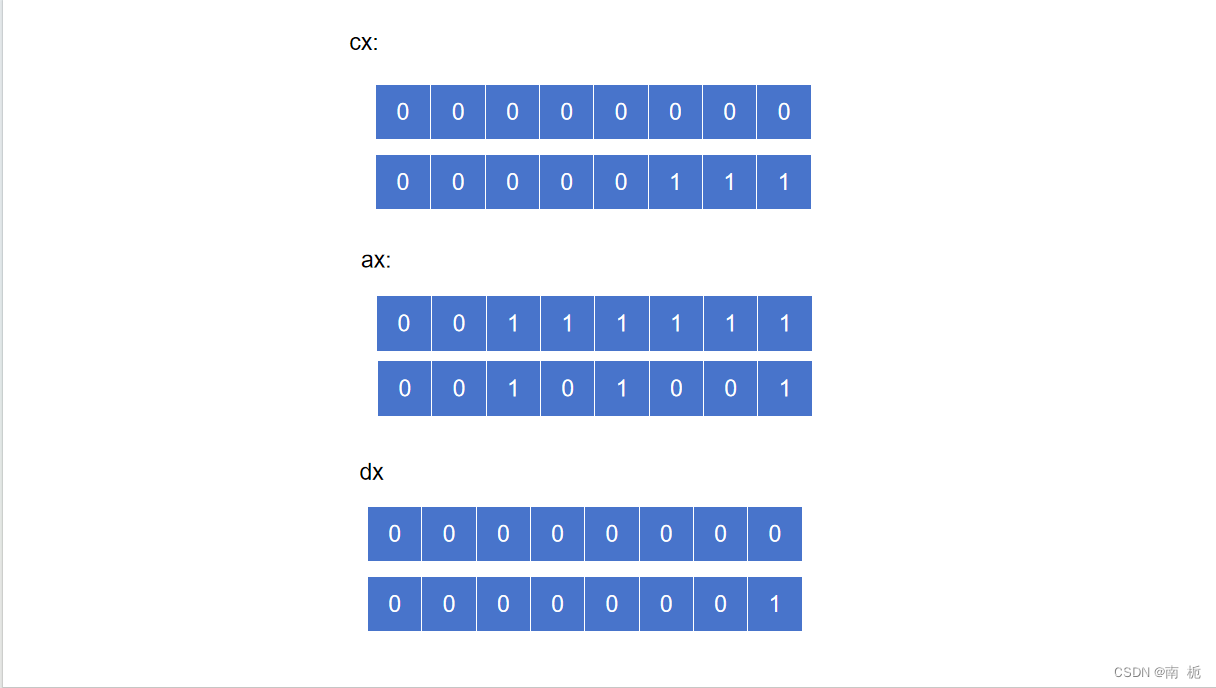
证明：16位的数据作为被除数计算的结果一定不会超过16位，因此第一次计算的结果一定不会溢出。第二次拿第一次的余数作为高位，低位不变进行计算，如何验证计算结果不会超过16位呢，证明如下。

低位<65535
高位%除数<=(除数-1)
(高位%除数)*65535<=(除数-1)*65535
(高位%除数)*65535+低位<=(除数-1)*65535+65535
[(高位%除数)*65535+低位]/除数<=[(除数-1))*65535+65535]/除数
[(高位%除数)*65535+低位]/除数<=65535

完整代码如下：

assume cs:code,ds:data,ss:stack
data segment
   dividend dd 0db6cah  ;存放被除数
   divisor dw 0bh       ;存放除数
   result dw 3 dup (0)  ;存放计算结果（结果和余数）
data ends

stack segment
    db 16 dup (0)
stack ends

code segment
start: 
    mov ax,data
    mov ds,ax
    mov ax,stack
    mov ss,ax
    mov sp,16
    call divdw
    ;.....
    mov ax,4c00h
    int 21h

divdw:
   mov ax,dividend[0]   
   push ax
   mov ax,dividend[2]
   mov dx,0
   mov cx,divisor[0]
   div cx
   mov bx,ax
   pop ax
   div cx

   mov cx,dx
   mov dx,bx

   mov result[0],ax
   mov result[2],dx
   mov result[4],cx
   mov ax,result      ;ax存储返回数据的地址
   ret
   
code ends
end start

总结：本质上采用将被除数缩小的思想进行计算。