目录
定义
递归
三种方法
1.hoare法
2.挖坑法
3.双指针法
整体
优化1
优化2
非递归
定义
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中 的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。
说人话就是将数组中任意一个元素作为基准值，将比基准值小的元素放在基准值的左边，将比基准值大的元素放在基准值的右边，经过不断的排序，实现将所有数据排序。
递归
三种方法
在我们完成整体的排序前，我们先考虑一下单趟是如何实现的（本篇文章皆考虑升序）
1.hoare法
顾名思义，就是快排提出人本身使用的方法
简单来说，就是从数组的两边，分别寻找比基准值大的数和比基准值小的数，在两侧都找到之后，进行交换。
而为了方便，我们常常使用左右两侧其中一个作为基准值（采用左侧）。而当我们采用左侧为基准值时，我们需要先在右侧寻找较小值，同理，在我们采用右侧为基准值时，我们需要在左侧寻找最小值，具体原因后面会提到。
例如下面的数组
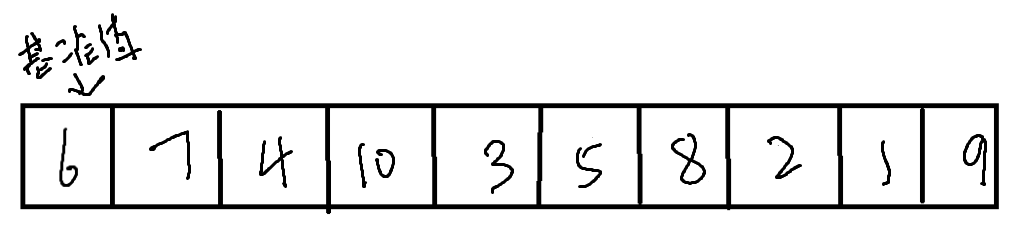
我们需要先进行不断得交换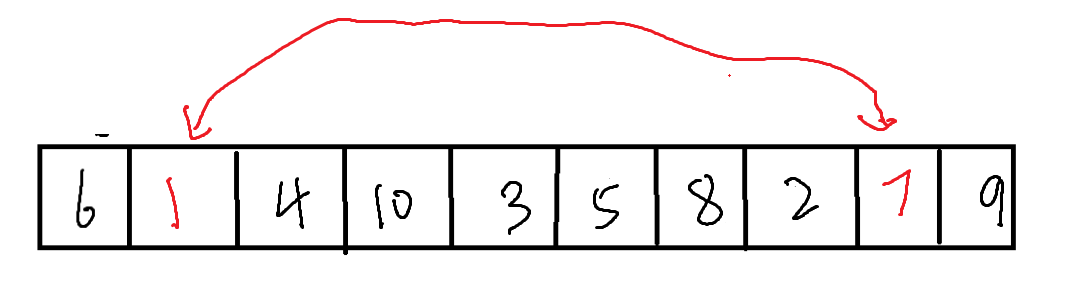
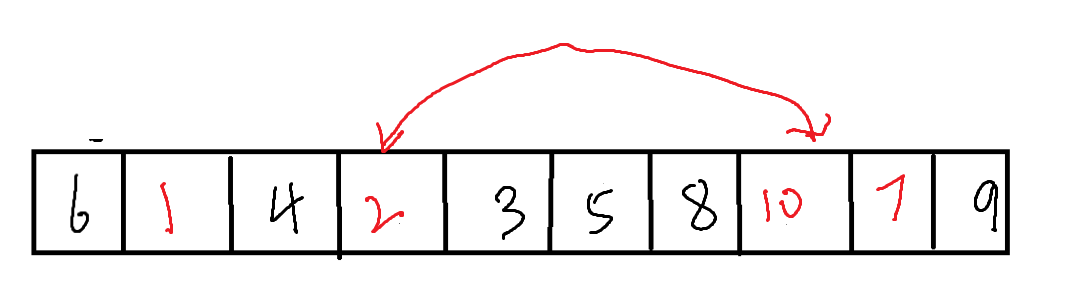
而这时，右侧（8）先寻找较小值，可以找到为5，而左侧（3）寻找较大值时会与右侧相遇。
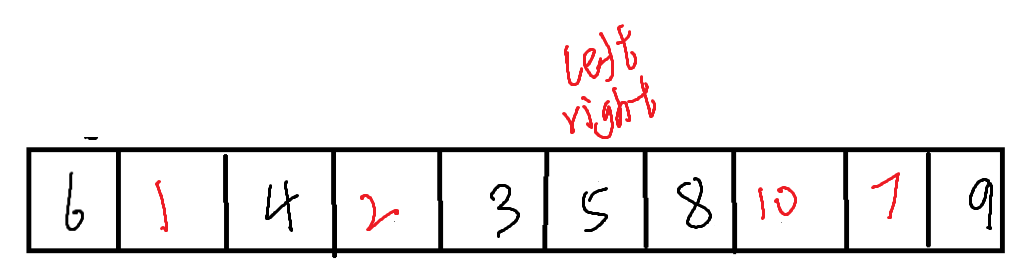
而在相遇后，由于我们是让右侧先走，因此我们可以发现，停下来的位置是比基准值小的，而后面的位置都是比基准值大的，因此，我们在这里将停下来的位置（left/right）与基准值的位置进行交换。
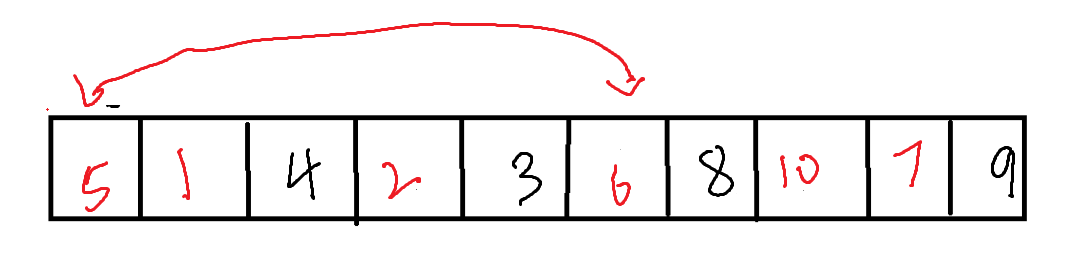这样便完成了一趟排序。
int Partion1(int* a, int left, int right)
{
int keyi = left;
while (left < right)
{
while (left < right && a[right] >= a[keyi])
--right;
while (left < right && a[left] <= a[keyi])
++left;
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
return left;
}2.挖坑法
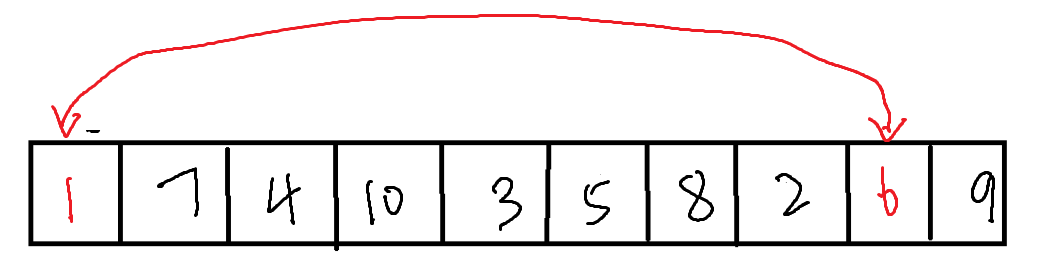
首先，我们选择左侧为一个坑位
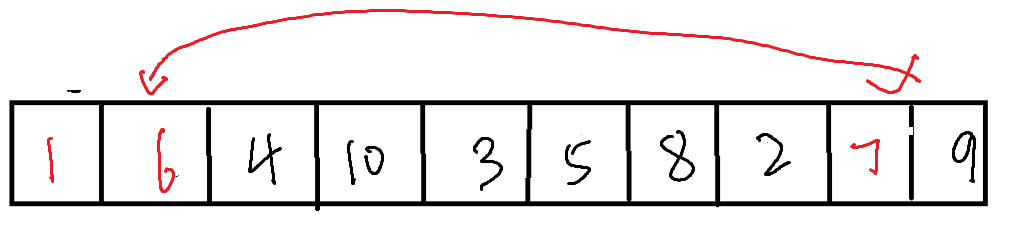
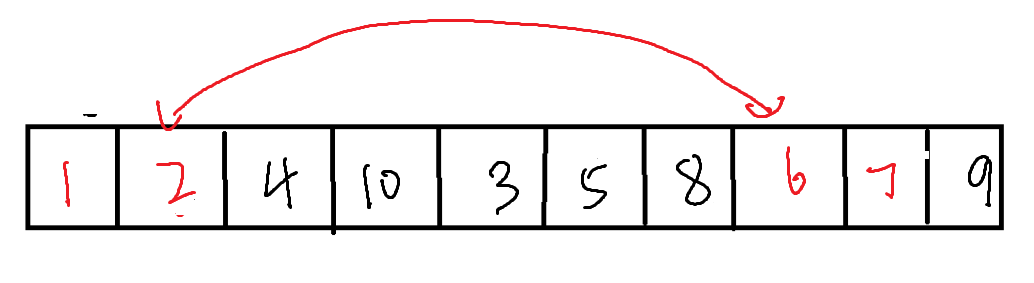
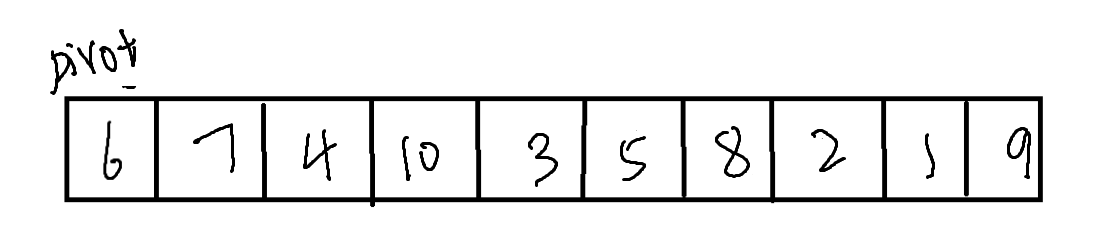之后从右侧开始，寻找比坑位内数值小的数据，使之与坑位内的数值交换，同时坑位也进行交换。之后，在从左侧（原本坑位所在的位置）向右寻找比坑位内数值大的数据，与坑位交换，依次进行。
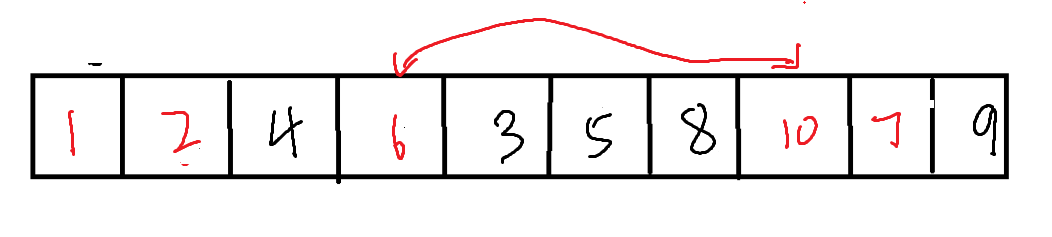
而当左侧或右侧与坑位相遇时，一趟排序便已经完毕。
int Partion2 (int* a, int left, int right)
{
int pivot = left;
while (left < right)
{
while (left < right && a[right] >= a[pivot])
right--;
Swap(&a[right], &a[pivot]);
pivot = right;
while (left < right&& a[left] <= a[pivot])
left++;
Swap(&a[left], &a[pivot]);
pivot = left;
}
return pivot;
}3.双指针法
我们需要两个指针prev和cur，初始时，prev指向左侧，cur指向左侧的下一个。
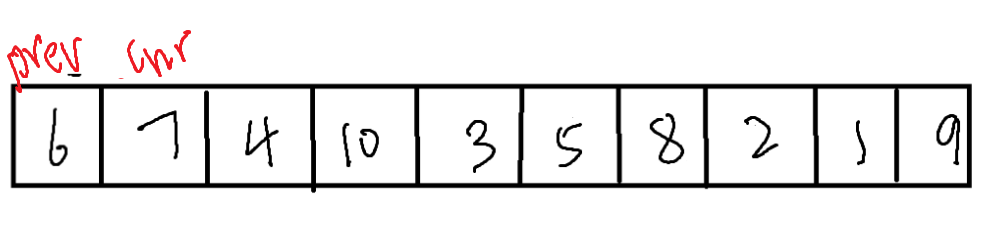
cur需要不断得bi向右进行便利，每当遇到比基准值（左侧数据）小的值时，将prev向右移动一位，并与cur位置的值进行交换。直到cur抵达右侧。
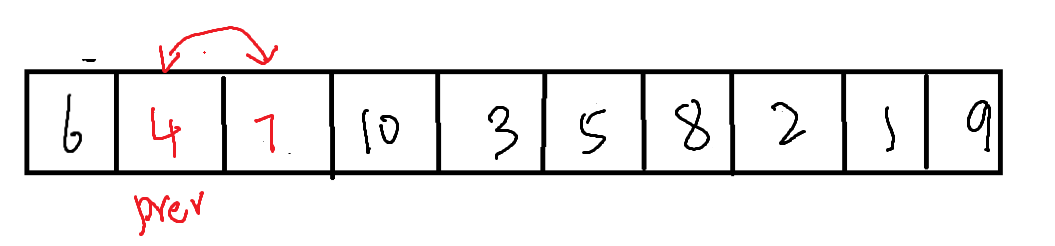
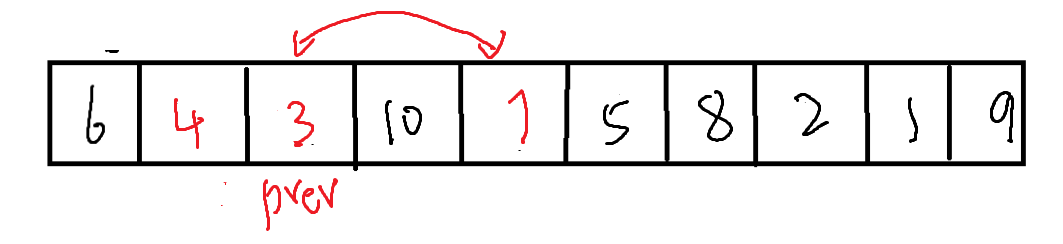
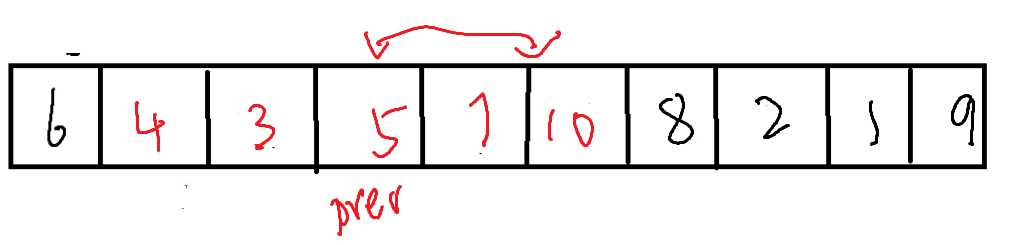
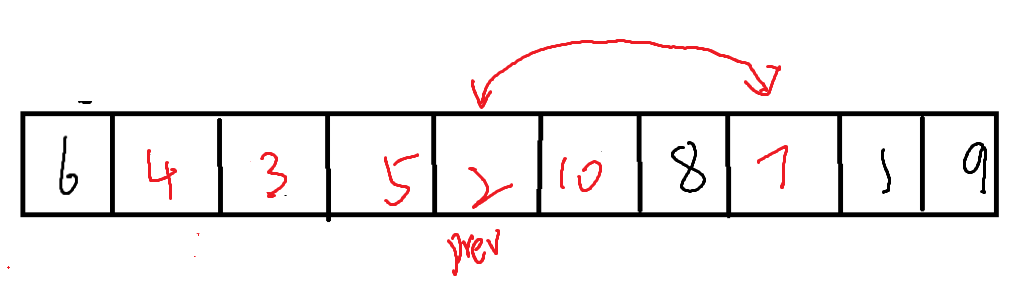
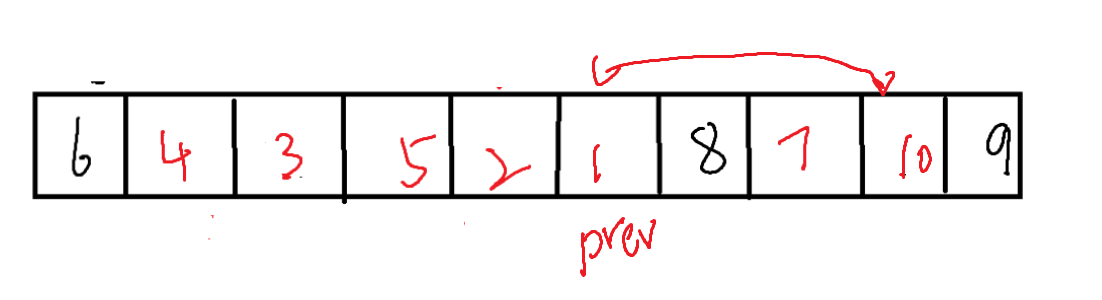
而在cur抵达右侧时，便只需要将左侧（基准值）与prev所在位置的值进行交换
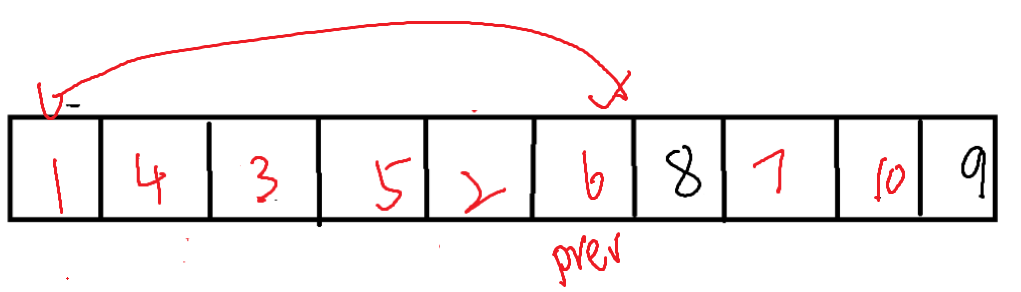
同时，我们也可以进行一些小小的优化，例如在prev与cur指向同一位置时不需要交换
最后便如下所示
int Partion3(int* a, int left, int right)
{
int keyi = left;
int prev = left;
int cur = left;
while (cur < right)
{
cur++;
if (a[cur] < a[keyi])
{
prev++;
if(cur!=prev)
Swap(&a[cur], &a[prev]);
}
}
Swap(&a[keyi], &a[prev]);
return prev;
}整体
在上面，我们提到了单趟排序的三种方法，而在我们结束单趟排序后，需要对基准值所在位置的左右两个区间的数据进行排序，直到这些区间的大小为0。我们便可以依此来完成整个的快排
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
int keyi = Partion1(a, left, right);
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}优化1
在写完整体的代码之后，我们可以发现，当keyi越接近区间的中间时，递归的次数就越少，因此，我们应该想办法使他位于区间的中间，即让单趟排序中的基准值的数值接近所有数据的中间位置。
但我们无法做到选择出一个完全接近中间的值，这也会消耗大量的时间，所以我们选择左侧、右侧、中间三个位置中数值不大不小的作为基准值，并将其放置在右侧。
int GetMidIndex(int* a, int left, int right)
{
int mid = left + (right - left) >> 1;
if (a[left] > a[mid])
{
if (a[right] < a[mid])
return mid;
else if (a[left] > a[right])
return right;
else
return left;
}
else
{
if (a[right] < a[left])
return left;
else if (a[mid] > a[right])
return right;
else
return mid;
}
}
int Partion1(int* a, int left, int right)
{
int mini = GetMidIndex(a, left, right);
Swap(&a[mini], &a[left]);
int keyi = left;
//......
}
同时，补充一个小知识点。我们可以看到，在我们寻找中间位置时，我们采用的是这样一个方法
int mid = left + (right - left) >> 1;这是因为，计算机计算时本质都是加法，在使用除法时也要转换为加法来计算，而这种方法效率更高。
优化2
在区间比较小的时候，快排依旧需要多层递归来完成排序，这时效率就不及其他排序了，因此，我们可以在其中加以判断，当区间（right-left）小于一个值时(可以为10)，就采用其他排序来完成，例如我们之前所提到的效率较高的希尔排序，这里就不多做赘述。
非递归
在写完递归后，我们可以尝试一下非递归的写法。
首先，由于每一层递归都有所不同，我们难以轻易的写出来。
而每一层递归都需要有一个区间，我们这里采用栈来进行存储。
首先我们将整个区间存储进去
ST stack;
StackInit(&stack);
StackPush(&stack, left);
StackPush(&stack, right);存储过后，我们还是采用上面的三种方法进行排序，而排序的区间改为从堆中删除的前后两个坐标
int end = StackTop(&stack);
StackPop(&stack);
int begin = StackTop(&stack);
StackPop(&stack);
int keyi = Partion3(a, begin, end);在递归中，我们在进行完一趟排序后，对 (left, keyi - 1)、(keyi + 1, right)两个区间进行下一步排序，而在这里，我们将这两个区间再次存储在栈中
StackPush(&stack, begin);
StackPush(&stack, keyi - 1);
StackPush(&stack, keyi + 1);
StackPush(&stack, end);之后通过循环进行再次的排序和存储。
而在两个区间的大小为0时，我们便不需要再进行这两个区间的存储
if (begin < keyi - 1)
{
StackPush(&stack, begin);
StackPush(&stack, keyi - 1);
}
if (keyi + 1 < end)
{
StackPush(&stack, keyi + 1);
StackPush(&stack, end);
}因此，循环的终止条件也就应该为栈中不存在数据
while (stack.top)如此，我们便能完成整个排序的编写
void QuickSortNonR(int* a, int left, int right)
{
ST stack;
StackInit(&stack);
StackPush(&stack, left);
StackPush(&stack, right);
while (stack.top)
{
int end = StackTop(&stack);
StackPop(&stack);
int begin = StackTop(&stack);
StackPop(&stack);
int keyi = Partion3(a, begin, end);
if (begin < keyi - 1)
{
StackPush(&stack, begin);
StackPush(&stack, keyi - 1);
}
if (keyi + 1 < end)
{
StackPush(&stack, keyi + 1);
StackPush(&stack, end);
}
}
StackDestroy(&stack);
}
