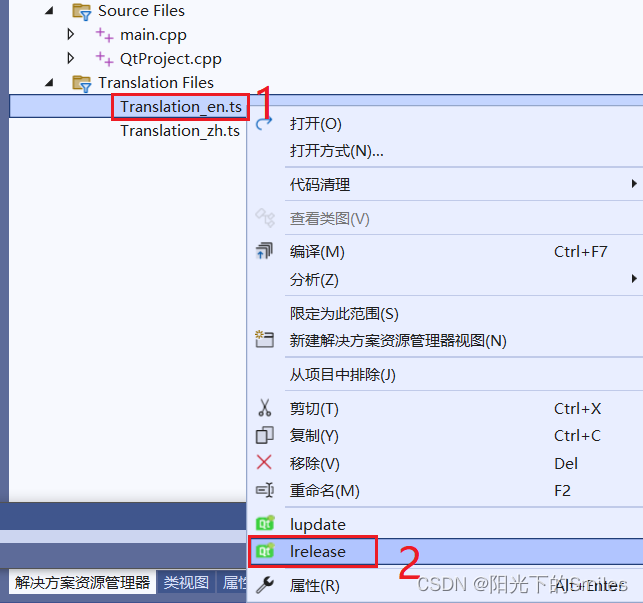
Park K, Sinha U, Barron J T, et al. Nerfies: Deformable neural radiance fields[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. 2021: 5865-5874.

Nerfies 是 Keunhong Park 在 Google 实习时基于 NeRF 模型开发的 可变形神经辐射场 (Deformable neural radiance fields)，它能够使用手机随意拍摄的照片或视频，以逼真的方式重建非刚性的可变形场景。

Nerfies 较 NeRF 的改进就是能够处理非刚性变形场景，尤其是手机自拍得到的短视频。通过额外优化一个连续的变形场，可以将每个观测点映射到 NeRF 标准空间下，并且引入了由粗到细优化和弹性正则增强鲁棒性，可以将随意的自拍照片或视频转为 Nerfies，做任意新视图渲染。

一. 研究思路

• 3D 人体扫描需要专业的设备和实验室，如果使用手机自拍就可以实现将会有很广阔的应用前景。
• 但使用手持相机自拍进行 3D 扫描建模有较大困难：因为我们不可能保持静止不动，而且头发、眼镜、耳环等违反了三维重建的假设 ¹，增加了重建的难度。
• 文章提出了基于 NeRF 的 变形 (deformation) 建模方法，可以使用自拍短视频进行高质量的三维重建，提供自由视角下的可视化，并且能够精准捕捉头发、眼镜等建模较为困难的部位。

1. 可变形神经辐射场

为了建模 非刚性变形 (non-rigidly deforming scenes) 场景，文章在标准 NeRF 的基础上引入一个额外的组件：变形场 (deformation field)，用于将 观测参照系 (observation frame) 中的三维坐标点 扭曲 (warp) 到标准 NeRF 模型的参照系中。由于不同观测视角扭曲到标准 NeRF 的情况不同，因此每个观测视角都设置一个变形场。变形场也用多层感知器 (MLP) 表示，通过学习该视角下图像的隐分布得到，不同视角的变形场各不相同。

非刚性 (non-rigidly)：指物体不是刚体（保持刚性形状且只能平移或旋转），可以发生非线性、弯曲、变形等形式的运动或变化。比如一个人在自拍时，身体的许多部位都可以动，而不是整个人的所有部位之间保持相对静止。
变形 (deforming)：指非刚性物体的形状或结构发生了变化。

2. 优化工作

为了稳健地对变形场进行优化，文章提出了一种由粗到细的优化方案（思想类似 NeRF 中渲染新视图时的分层抽样），通过频率调整变形场网络中输入的位置编码。优化开始时将高频归零，网络只能学习平滑的变形情况；然后逐渐引入高频进行细化。

二. 可变形神经辐射场

为了建模非刚性变形场景，文章中将场景分解为一个 NeRF 表示的 模板体 (template volume) 和每个观测视角上一个的变形场。变形场负责将观测参照系中的三维坐标点与模板体中的点进行关联，是扩展 NeRF 表示非刚性物体的关键。

从每个视角的隐空间中提取各自的变形码 $\omega$ 和外观码 $\psi$，变形码 $\omega$ 用于构建该视角下的变形场，外观码 $\psi$ 用于处理特定视角下的颜色和外观变化。 在观测参考系中追踪摄像机光线的轨迹，使用变形场将光线上的采样点 $(x,y,z)$ 扭曲到标准 NeRF 模型中得到 $(x^{\prime },y^{\prime },z^{\prime })$。渲染视图时使用转换后的样本 $(x^{\prime },y^{\prime },z^{\prime })$、观察方向 $(\theta ,\phi )$ 和外观码 $\psi$ 作为输入传入模板 NeRF，并沿着光线对样本进行积分。

1. 神经辐射场

关于神经辐射场 NeRF 的详细介绍见 NeRF：将场景表示为神经辐射场以用于视图合成。但 NeRF 的采样过程要求场景不发生变形，而人们在摆姿势拍照时很难保持姿势不变。

本文使用 NeRF 作为场景的规范模板，用于表示场景的相对结构和外观，而渲染时则使用模板的非刚性变形版本。

2. 神经变形场

每个观测视角 $i$（ i ∈ { 1 , 2 , … , n } i \in \{1, 2, \dots, n\} i∈{1,2,…,n}）处应用一个变形场，用于将观测域中的坐标扭曲到模板域中，该映射记为：
$$T_i:\mathbf{x}\to {\mathbf{x}}^{\prime }$$
于是整个场景内所有视角下的变形场的映射可以表示为：
$$T:(\mathbf{x},{\omega }_i)\to {\mathbf{x}}^{\prime }$$

若给定标准域 $F$ 和观测域到标准域的映射 $T$，则渲染结果可以表示为：
$$G(\mathbf{x},\mathbf{d},{\psi }_i,{\omega }_i)=F(T(\mathbf{x},{\omega }_i),\mathbf{d},{\psi }_i)$$

渲染时只需简单地在观测视角处发射光线并沿着光线取采样点，然后使用变形场将采样点映射到模板上。

三. 优化工作

由于 NeRF 模板体和变形场都是由多层感知机表示，如果一起优化会出现 欠约束的优化问题 (under-constrained optimization problem)。因此，文章引入了变形场景的弹性正则化、背景正则化，以及由粗到细的连续退火技术。

欠约束的优化问题 (under-constrained optimization problem)：优化过程中有太多的自由度或变量，但约束条件相对较少，因此可能存在多个可能的解决方案，即约束条件不足以唯一确定一个最优解。在这种情况下，优化算法可能会产生多个合理的解决方案，或者难以找到一个满足所有约束条件的解决方案。

1. 弹性正则化

变形场增加了优化过程中的不确定性。因此在处理非刚性物体变形时，通常引入 弹性能量 (elastic energy) 来捕捉局部形状的非刚性特性，文中通过弹性能量测量局部变形与刚性运动的偏差。

通过计算局部变形场的雅可比矩阵 (Jacobian)，可以控制局部变形行为。此外，有多种方法计算雅可比矩阵与最优旋转矩阵之间的差异 ²，作者选择使用雅可比矩阵的奇异值并测量其与单位矩阵的差异。这种方法通过对奇异值的对数来平衡扩展和收缩，从而实现更好的性能：
$$L_{\text{elastic }}(\mathbf{x})=\Vert \log \mathbf{\Sigma }-\log \mathbf{I}{\Vert }_F^2=\Vert \log \mathbf{\Sigma }{\Vert }_F^2$$

2. 背景正则化

由于变形场不受约束，因此一些本该保持静止的物体也可能发生变形。为了防止这些物体的变形，文章引入了正则化项以限制它们的运动，从而保持其在场景中的固定位置。给定一组静态的三维空间点 { x 1 … , x K } \{\mathbf{x}_1 \ldots, \mathbf{x}_K\} {x1​…,xK​}，定义防止变形的正则项为：
$$L_{\mathrm{bg}}=\frac{1}{K}\sum _{k=1}^K{\Vert T\left({\mathbf{x}}_k\right)-{\mathbf{x}}_k\Vert }_2$$

该正则项不仅可以防止背景点的移动，还有助于将观测域与模板域对齐。

3. 由粗到细的变形场正则化

在配准和流估计过程中出现的一个常见问题就是在建模微小变形和大型运动之间的权衡，这可能会导致过度平滑的结果或不正确的配准（局部极小值）。文章中使用一个由粗到细的正则化来缓解。

配准（Registration）：将两个或多个图像或数据集的内容进行对齐，以便它们在相同的坐标系中可进行比较或叠加。配准通常用于将不同视角或时间点的图像或数据对准，以便进行对象跟踪、目标检测、图像融合等应用。
流估计（Flow Estimation）：在连续帧图像之间估计表面上各点的像素位移，用于捕捉对象或场景中的像素级运动信息。流估计用于跟踪对象的运动、分析相机的运动、检测运动物体等应用。

NeRF 在位置编码时使用的超参数 $m$ 可以控制编码中的频带数量（即编码的精细程度），用于控制网络的平滑度。$m$ 的值越小，编码中包含的高频信息越少，结果看起来平滑但图像分辨率越低；$m$ 的值越大，编码中包含的高频信息越多，图像分辨率越高。

频带数量：可以理解为编码的精细程度，即在使用某种编码方法表达数据时包含了多少细节或高频信息。频带数量越多，精细程度越高，表示的数据越具有细节、高频特征，反之亦然。

如上图中所示，变形场的 $m$ 值较小时模型无法捕捉微笑的微小变形；$m$ 较大时模型不能正确旋转头部，因为模板过度拟合到一个未优化的变形场。因此需要选择适当的编码精细度来平衡图像或数据的平滑度和细节捕捉。为此，论文提出从低频偏差开始到高频偏差结束的由粗到细的方法。更多细节见 26、Nerfies:Deformable Neural Radiance Fields。

四. 实验结果

1. 实现细节

• 模板 NeRF：同原始 NeRF 模型，并在计算体积密度时使用了 Softplus 激活函数 $ln(1+e^x)$。
• 变形场：深度 6，隐藏层大小 128，并在第 4 层增加了跳跃连接。
• 光线采样：256 个粗细光线采样，全高清 (1920×1080) 模型。
• 隐变量：8 维变形码和外观码。
• 训练资源：8 块 V100 GPU 训练，全高清模型需一周，半分辨率模型需 16 小时。

2. 数据集

3. 模型评价

见 26、Nerfies:Deformable Neural Radiance Fields

五. 总结

Nerfies 首创性地实现了使用手机随意拍摄的照片或视频真实重建非刚性变形场景的方法。通过额外优化一个变形场，将每个观察样本点扭曲成标准的 5D NeRF 坐标。

六. 复现

Nerfies 并不基于 Pytorch 或 Tensorflow，而是使用 JAX 实现的，构建于 JaxNeRF 之上。

• 平台：Google Colab
• 源码：https://github.com/google/nerfies

实验记录：

1. 第一次执行 Nerfies Capture Processing v2.ipynb 时上传的视频为 https://nerfies.github.io/static/videos/chair-tp.mp4，执行到 Reconstruction 时报错捕获图像数量不够，改为上传 https://nerfies.github.io/static/videos/teaser.mp4 的视频；

实验结果：

---

1. 3D视觉基础 ↩︎

2. 论文随记｜Nerfies:Deformable Neural Radiance Fields ↩︎