1、内容简介
略
5-可以交流、咨询、答疑
2、内容说明
Spongent 是一种轻量级 Hash 算法,其原理与“海绵”类似,分为“吸收”
和“榨取”两个阶段,所以又可以称之为“海绵结构”算法。
Hash 函数之所以有广泛的应用,是因为它具有以下几个性质:
(1)单向性,对于任意的 Hash 码 h,找到能使 H(x)=h 成立的 x 在计算上是
不可行的。
(2)抗弱碰撞性,对于任意的 x,找到能使 H(x)=H(y)成立的 y 在计算上是不
可行的。
(3)抗强碰撞性,对于任意指定的 Hash 算法,想找到不同的输入得到相同的
输出是不可行的。
下面简单的介绍一下 Spongent 算法的原理。
Spongent 算法是 Bogdanov 等人在 CHES 2011 上提出的轻量级 Hash 函数。
Spongent 算法用 Spongent-n/c/r 表示,是由迭代函数 Spongent-
ߨ
ܾ
、比特率 r、
容量 c、轮数 R 等组成的海绵结构的算法。给定有限数量的输入位,它将产
生一个 n 位的哈希值。在 Spongent-
ߨ
ܾ
中,b 作为置换位的宽度,即 state 结
构的容量,b=c+r。Spongent 算法的加密步骤如图 1 所示
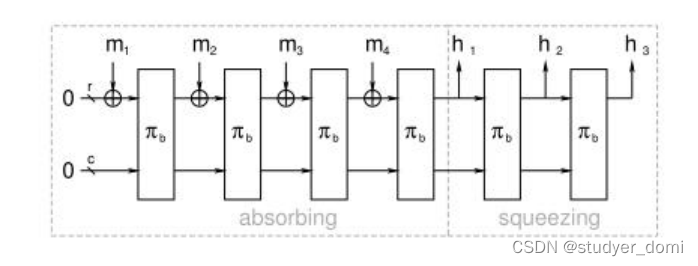
从图中可以看出 Spongent 算法的“吸收”和“榨取”过程。具体加密步骤
及各模块内部结构及运算方法如下:
1、初始化阶段:
该输入数据将由一个单一的位 1 填充,后跟必要数量的 0 位,位数
直 到 达 到 r 位 的 倍 数 ( 例 如 , 如 果 r=8, 则 1 位 消 息 “0”将 转 换 为
“01000000”)。然后将其切成 r 位的块。简单举例来说,如果 r=8,而
有一个输入数据是 10 位,那么在此数位最右边补上一个单一的 1 后,
用 0 来将其填充至 r=8 的最小倍数数位 16。因为 r=8,所以位数为 16
的数据不能一次性输入(为什么不能一次性输入后面详谈),应该分为
数据块依次输入。因为是 8 的整倍数,所以将其分为 p=16/8=2 数据块
来进行输入。其他位数的数据同样是这种处理方法。简单来说就是,令
|m|为经过填充处理的数据 m 的长度,则 p=|m|/r。
2、吸收阶段:
如图 1 所示,比特率 r 和容量 c 初始数据都为 0,图 1 中所示的
݉
ͳ
、
݉
ʹ
、
ǥ
、
݉
݅
为初始化阶段中对处理后的输入数据 m 分块处理后的结果,例如初始化阶段所
举例子经过填充处理位数为 16 的数据经过分块处理后,分为了两个数据块,那
么位数为 16 的数据在输入阶段就对应着
݉
ͳ
、
݉
ʹ
两段输入,以此类推。如图 1
所示,很清楚的可以知道,被分块后
݉
ͳ
首先与状态值(state)的前 r 位的值进
行异或运算(state 的位数为 b,而 b=r+c,此处前 r 位的值为 0,前面举例 r=8
是指 r 的位数为 8,而 r 的初值都是 0,如果说 r=8,就是指 r 为 8 位的全 0 数
据,即“00000000”),而后 c 位的值不与
݉
ͳ
进行异或运算,如图 1 所示,经过
异或运算后 b 位的新状态值(state)被送入
ߨ
ܾ
中进行运算(
ߨ
ܾ
中的运算很复杂,
后面进行讲解),得出运算过后的新 b 位状态值,同样,重复前一个步骤,因为
的分得的数据块的位数相同都是 r 位,再将新的状态值的前 r 位与数据块第二块
݉
ʹ
进行异或运算,后 c 位仍然不参加运算,得到的新状态值后再送入下一个
ߨ
ܾ
中(注:在 n/c/r 都相同的一个 Spongent 算法中,每一个
ߨ
ܾ
中的运算都是不一
样的,并不是相同的,不过他们的运算轮数都是一样的,后面会在对 Spongent-
ߨ
ܾ
的介绍中提到),以此类推,直到将 m 所分的块全部都进行输入完为止,即若分
块为
݉
ͳ
、
݉
ʹ
、
ǥ
、
݉
݅
,则一直到
݉
݅
输入并进行运算后,吸收阶段才会结束,如
图 1 所示。
3、榨取阶段:
如图 1 所示,榨取阶段的原理其实和吸收阶段的原理近似相同,对数据进行
置换的函数依旧是 Spongent-
ߨ
ܾ
,只不过没有吸收阶段的异或过程,榨取阶段的
第一个输入为吸收阶段的最后一个置换函数
ߨ
ܾ
的输出,因为吸收与榨取阶段的置
换函数类型相同(内部运算不同),所以其输入输出都是 b 位的状态值,榨取阶段
每次
ߨ
ܾ
输出 b 位状态值,取其前 r 位作为输出
݄
݅
,同时将此次置换函数输出的 b
位状态值作为下一个置换函数
ߨ
ܾ
的输入,以此类推。对于不同的 Spongent 算法
类型,榨取阶段输出 r 位的组数也不同,已知 Spongent-n/c/r 中的 n 为算法的
最终输出数据的位数,所以需要 j=|n|/|r|组置换函数的输出。例如,对于
Spongent-88/80/8 来说,r=8,n=88,则榨取阶段应该输出 j=|n|/|r|=88/8=11
个 r=8 比特的数据组再将每一次的输出
݄
ͳ
、
݄
ʹ
、
ǥ
、
݄
ͳ ͳ
整合为 n=88 位的输出数
据,如图
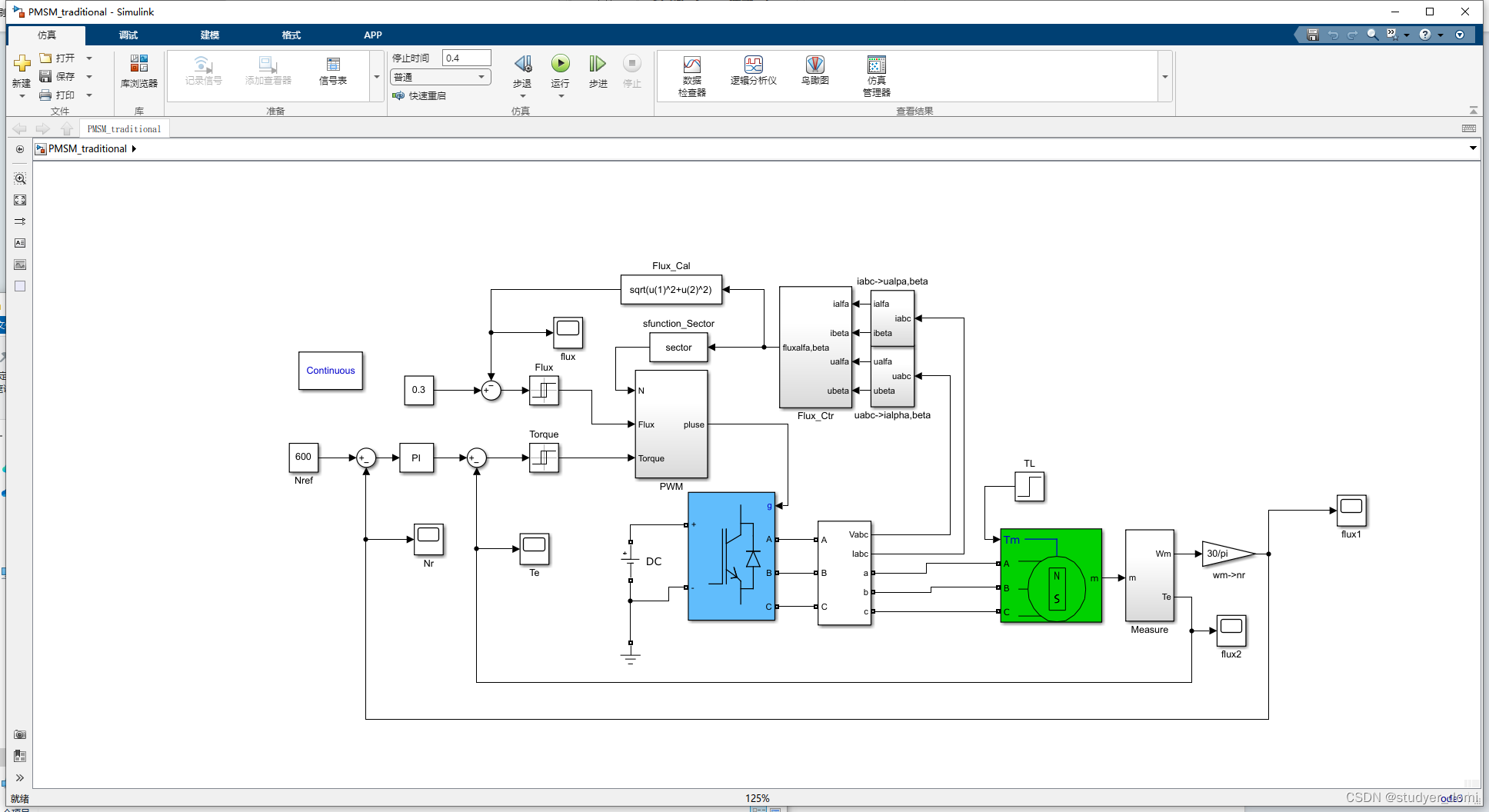
3、仿真分析
4、参考论文
略