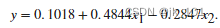损失函数总结(三):BCELoss、CrossEntropyLoss
- 1 引言
- 2 损失函数
- 2.1 BCELoss
- 2.2 CrossEntropyLoss
- 3 总结
1 引言
在前面的文章中已经介绍了介绍了一系列损失函数 (L1Loss、MSELoss)。在这篇文章中,会接着上文提到的众多损失函数继续进行介绍,给大家带来更多不常见的损失函数的介绍。这里放一张损失函数的机理图:

2 损失函数
2.1 BCELoss
BCELoss(Binary Cross-Entropy Loss,二进制交叉熵损失)是一种用于二分类任务的损失函数,通常用于测量模型的二分类输出与实际标签之间的差距。BCELoss的数学表达式如下:
L
BCE
(
y
,
y
′
)
=
−
1
n
∑
i
=
1
n
[
y
i
log
(
y
i
′
)
+
(
1
−
y
i
)
log
(
1
−
y
i
′
)
]
L_{\text{BCE}}(y, y') = -\frac{1}{n} \sum_{i=1}^{n} [y_i \log(y_i') + (1 - y_i) \log(1 - y_i')]
LBCE(y,y′)=−n1i=1∑n[yilog(yi′)+(1−yi)log(1−yi′)]
其中:
-
L
BCE
(
y
,
y
′
)
L_{\text{BCE}}(y, y')
LBCE(y,y′) 是整个数据集上的二进制
交叉熵损失。 - n n n 是样本数量。
-
y
i
y_i
yi 是第
i
i
i 个样本的
实际标签,通常是0或1(表示两个类别中的一个)。 -
y
i
′
y_i'
yi′ 是第
i
i
i 个样本的模型预测的
概率,通常在0和1之间。
代码实现(Pytorch):
m = nn.Sigmoid()
loss = nn.BCELoss()
input = torch.randn(3, requires_grad=True)
target = torch.empty(3).random_(2)
output = loss(m(input), target)
output.backward()
BCELoss 常用于二分类任务,是二分类任务中常见的损失函数之一。二分类任务如:垃圾邮件检测(是垃圾邮件还是非垃圾邮件)或医学图像分类(是病态还是正常)
2.2 CrossEntropyLoss
CrossEntropyLoss(交叉熵损失)通常用于多类别分类任务,它是一种用于度量模型的类别概率分布与实际类别分布之间的差距的损失函数。CrossEntropyLoss 的数学表达式如下:
L
CE
(
Y
,
Y
′
)
=
−
1
n
∑
i
=
1
n
∑
j
=
1
C
y
i
j
log
(
y
i
j
′
)
L_{\text{CE}}(Y, Y') = -\frac{1}{n} \sum_{i=1}^{n} \sum_{j=1}^{C} y_{ij} \log(y_{ij}')
LCE(Y,Y′)=−n1i=1∑nj=1∑Cyijlog(yij′)
其中:
-
L
CE
(
Y
,
Y
′
)
L_{\text{CE}}(Y, Y')
LCE(Y,Y′) 是整个数据集上的
交叉熵损失。 - n n n 是样本数量。
- C C C 是类别数量。
-
y
i
j
y_{ij}
yij 是第
i
i
i 个样本的实际类别分布,通常是一个
独热编码(one-hot encoding)向量,表示实际类别。 -
y
i
j
′
y_{ij}'
yij′ 是第
i
i
i 个样本的模型预测的类别概率分布,通常是一个
概率向量,表示模型对每个类别的预测概率。
代码实现(Pytorch):
# 带有类别索引的目标示例
loss = nn.CrossEntropyLoss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.empty(3, dtype=torch.long).random_(5)
output = loss(input, target)
output.backward()
# 带有类别概率的目标示例
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5).softmax(dim=1)
output = loss(input, target)
output.backward()
CrossEntropyLoss 广泛用于多类别分类任务,例如图像分类(将图像分为多个不同的类别),自然语言处理(将文本分类到不同的类别),语音识别等领域。CrossEntropyLoss 损失函数是当前多分类任务的标准方法。
3 总结
到此,使用 损失函数总结(三) 已经介绍完毕了!!! 如果有什么疑问欢迎在评论区提出,对于共性问题可能会后续添加到文章介绍中。如果存在没有提及的损失函数也可以在评论区提出,后续会对其进行添加!!!!
如果觉得这篇文章对你有用,记得点赞、收藏并分享给你的小伙伴们哦😄。