被研究最多的图像(或任何序列数据)变换域表示是通过傅
里叶分析
。所谓的傅里叶表示就是使用
正弦函数的线性组合来表示信号。对于一个给定的图像I(n1,n2)
,可以用如下方式分解它(即逆傅里叶变换):
 其中,I F(u,v)
是傅里叶系数,可以由如下方式(即傅里叶变换)得到:
其中,I F(u,v)
是傅里叶系数,可以由如下方式(即傅里叶变换)得到:

在这种表示中,像素表示的图像 I(n1,n2)被分解成频率分量。每个频率分量的系数描述该频率分量存在的多少 频率分量在这里成为表示图像的基础。这种方法的常见应用是 JPEG (]
o
in
t
Photographic
Experts
Group )图像压缩中用到的可变离散余弦变换(
Discrete
Cosine Transform,
DCT
JPE
编解码器仅使用式
(1.2)
中正弦曲线的余弦分量,因
此称为
离散余弦基
DCT
基函数如图
所示1-2所示

从像素表示到变换域表示的任何变换核都可以写成 b(n1,n2.u,v)
,逆向
变换写成的B
(n1,n2.u,v)
对于许多变换,这些基在数学上通常是可逆的,相 互之间可
以转换
从图像空间到基空间的映射或变换可以公式化为:
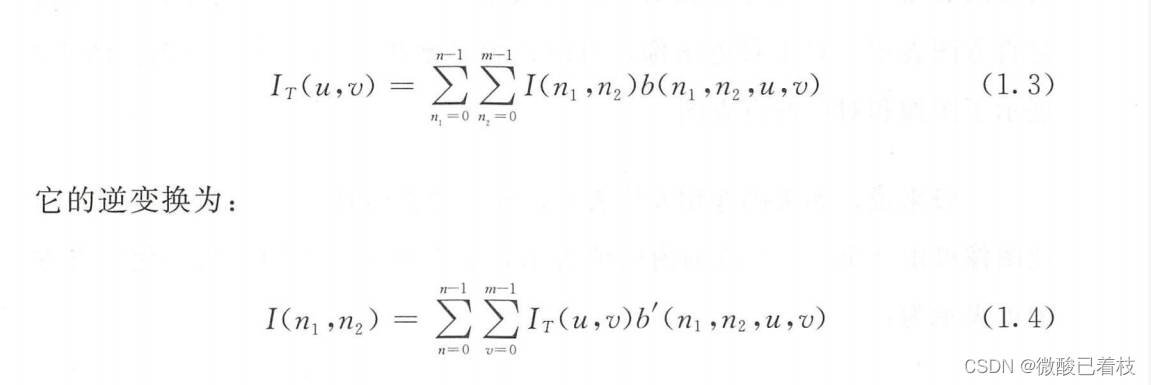
式(1.3)是式(1.2)的一般化。许多图像表示可以通过这种形式在变换域建模,傅里叶变换只是其中的一种特殊情况