目录
深度优先算法(Depth-First Search,DFS)
LeetCode之路——102. 二叉树的层序遍历
分析

深度优先算法(Depth-First Search,DFS)
DFS是一种用于遍历或搜索树状数据结构的算法,其中它首先探索树的深度,然后回溯并继续探索其他分支。在二叉树中,深度优先算法可以通过递归或使用栈来实现。有三种常见的深度优先遍历方式:前序遍历、中序遍历和后序遍历,每种方式都对节点的访问顺序略有不同。
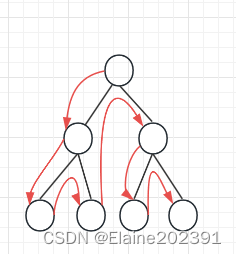
以下是深度优先遍历的Java代码示例,包括前序遍历、中序遍历和后序遍历:
class TreeNode {
int data;
TreeNode left;
TreeNode right;
public TreeNode(int data) {
this.data = data;
}
}
// 前序遍历(Preorder DFS)
void preorderDFS(TreeNode node) {
if (node == null) return;
System.out.print(node.data + " "); // 先访问根节点
preorderDFS(node.left); // 遍历左子树
preorderDFS(node.right); // 遍历右子树
}
// 中序遍历(Inorder DFS)
void inorderDFS(TreeNode node) {
if (node == null) return;
inorderDFS(node.left); // 遍历左子树
System.out.print(node.data + " "); // 访问根节点
inorderDFS(node.right); // 遍历右子树
}
// 后序遍历(Postorder DFS)
void postorderDFS(TreeNode node) {
if (node == null) return;
postorderDFS(node.left); // 遍历左子树
postorderDFS(node.right); // 遍历右子树
System.out.print(node.data + " "); // 最后访问根节点
}
LeetCode之路——102. 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
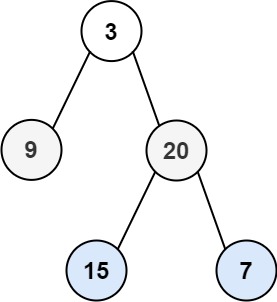
输入:root = [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1] 输出:[[1]]
示例 3:
输入:root = [] 输出:[]
提示:
-
树中节点数目在范围
[0, 2000]内 -
-1000 <= Node.val <= 1000
分析
逐层地,从左到右访问所有节点,这种情景叫做树的层序遍历。匹配的算法是DFS(Depth-first search)和BFS(Breadth-first search)。
// DFS算法-前序遍历
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> resList = new ArrayList<List<Integer>>();
dfsPreorder(root, 0, resList);
return resList;
}
/**
* 前序遍历的DFS
* @param node
* @param deep
*/
public static void dfsPreorder(TreeNode node, int deep, List<List<Integer>> resList) {
if (node == null) return;
deep++;
if (resList.size() < deep) {
// 用resList的索引标记层数
List<Integer> list = new ArrayList<>();
resList.add(list);
}
resList.get(deep - 1).add(node.val);
//左侧子节点遍历
dfsPreorder(node.left, deep, resList);
//右侧子节点遍历
dfsPreorder(node.right, deep, resList);
}
}
-
时间复杂度:O(n)
-
空间复杂度:O(n)