目录

2316. 统计无向图中无法互相到达点对数

题目描述：

实现代码与解析：

并查集

原理思路：

---

2316. 统计无向图中无法互相到达点对数

题目描述：

        给你一个整数 n ，表示一张 无向图 中有 n 个节点，编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。

请你返回 无法互相到达 的不同 点对数目 。

示例 1：

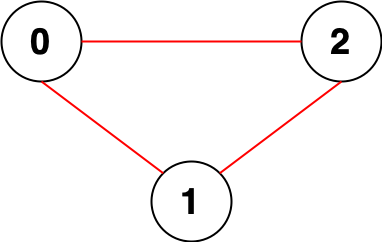
输入：n = 3, edges = [[0,1],[0,2],[1,2]]
输出：0
解释：所有点都能互相到达，意味着没有点对无法互相到达，所以我们返回 0 。

示例 2：

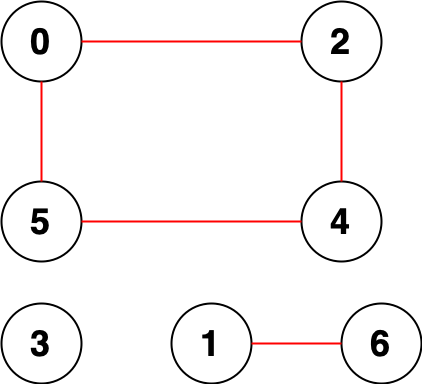
输入：n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
输出：14
解释：总共有 14 个点对互相无法到达：
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]]
所以我们返回 14 。

提示：

• 1 <= n <= 105
• 0 <= edges.length <= 2 * 105
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• 不会有重复边。

实现代码与解析：

并查集

class Solution {
public:
    vector<int> p = vector<int>(100000, 0);
    // 并查集
    int find(int x) {
        if (x != p[x]) p[x] = find(p[x]);
        return p[x];
    }

    long long countPairs(int n, vector<vector<int>>& edges) {
        
        unordered_map<int, int> map;

        for (int i = 0; i < n; i++) p[i] = i; // 初始化

        // 连接
        for (auto t: edges) {
            if (find(t[0]) != find(t[1])) p[find(t[0])] = find(t[1]);
        }

        // 记录连通分量根节点，和每个连通分量的节点个数
        for (int i = 0; i < n; i++) {
            int root = find(i);

            if (map.count(root)) {
                map[root]++;
            } else {
                map[root] = 1;
            }
        }

        // 遍历连通分量，      
        // 每次遍历cnt都减去，因为[0, 1][1, 0]属于同一种      
        int cnt = n; 
        long long res = 0;
        for (auto &[a, b]: map) {
            cnt -= b;
            res += 1ll * b * cnt; // 连通的 与 和 他不连通的 相乘，不算已经计算过的
        }
        return res;
    }
};

原理思路：

        并查集。

        如果没学过，可以看我之前写的并查集详解。Leetcode：684. 冗余连接（并查集C++）-CSDN博客

        这里，并查集算法后，计算连通分量，和每个连通分量含义节点个数，map存储。

然后计算结果：

 // 遍历连通分量，      
// 每次遍历cnt都减去，因为[0, 1][1, 0]属于同一种      
int cnt = n; 
long long res = 0; // 结果
for (auto &[a, b]: map) {
    cnt -= b;
    res += 1ll * b * cnt; // 连通的 与 和 他不连通的 相乘，不算已经计算过的
}
return res;