【MATLAB第79期】基于MATLAB的数据抽样合集（sobol、LHS拉丁超立方抽样、Halton、正交/均匀设计、随机rand函数）

一、传统函数

1.指定区间随机生成数据（小数）

[a b]区间随机数生成:
A=a+(b-a)rand(m,n)

m：待生成矩阵A的行数
n: 待生成矩阵A的列数

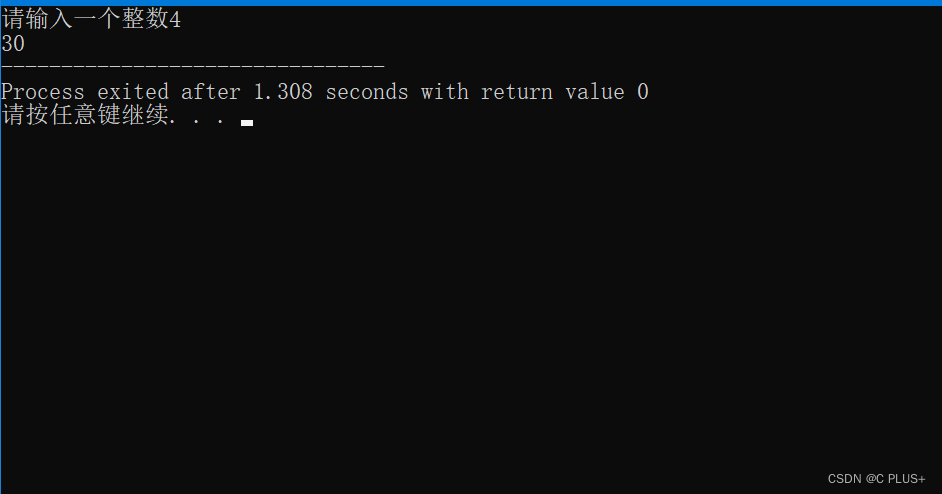
示例：生成-5到5之间的随机数

%生成随机数在[-5 5]范围内的2×2矩阵
a=-5;
b=5;
A=a+(b-a)*rand(2,2)

A =

      1.27          2.94
     -4.22          2.69

2.指定区间随机生成数据（整数）

randi - 整数均匀随机分布

A=randi([-5, 5], 2, 2) %-5到5均匀分布的2x2随机矩阵

A=

     -2.00          3.00
      1.00          4.00

3.指定数值及概率随机生成数据

randsrc - 生成指定范围的随机数

A = randsrc(2, 2, [-5 -2.5 0 2.5 5; 0.2 0.2 0.2 0.2 0.2])
% 在-5 -2.5 0 2.5 5五个数中随机选生成2x2的矩阵
后面的0.2是每个数对应的概率

A =

      2.50         -2.50
     -5.00          2.50

4.标准正态分布

randn - 标准正态分布

 A= randn(2, 2)        %标准正态分布的2x2矩阵

A =

      0.82          0.16
      0.73          0.10

二、正交/均匀试验设计

1.正交设计

每个正交表都有一个表头符号，记作LN（mk），表示该正交表有N行k列，每一列由整数1，2，…，m组成。

用表LN（mk）安排试验时，N表示试验次数/处理数，k表示最多可以安排的因素个数（分析因素），m表示各因素的水平数。

常用正交表：
https://www.docin.com/p-2228475212.html

举例：

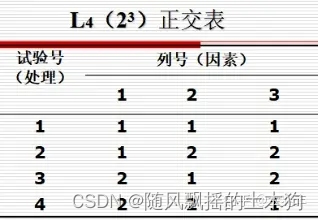
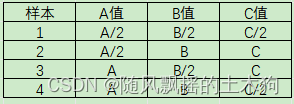
如果有三个变量，A B C，其次，每个变量两个水平（范围），即变量值的0.5和1倍。
则可以利用L4(2^3)正交表，得到4个样本。

2.均匀设计

均匀表与正交表类似。

常用均匀表：
https://www.docin.com/p-2646778286.html
举例：
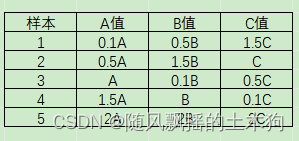
如果有三个变量，A B C，其次，每个变量五个水平（范围），即变量值的0.1、0.5、1、0.5、2倍。

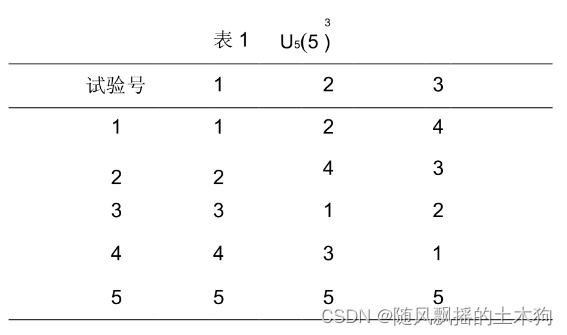
均匀设计结果：

三、SOBOL抽样

ndim=4;%维度为4
minX=[-1.75, 32.4, -1, -234.2];%下限
maxX=[ 3.95, 112.56, 9, 156.37];%上限
popsize=200;%样本数
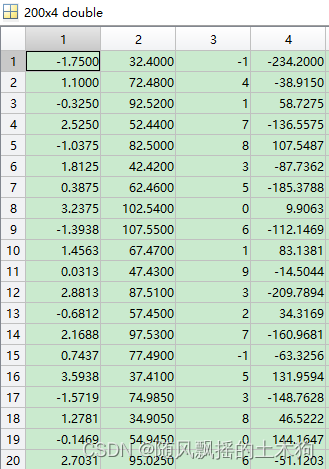
sobolset是一个准随机点集对象，它从Sobol序列中生成点。Sobol序列是以高度均匀的方式填充空间的基于2的数字序列。
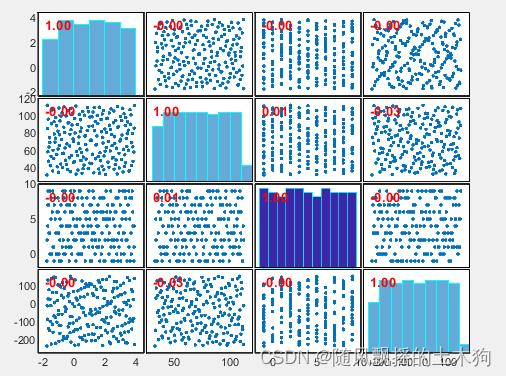
sobol函数结果（其中对变量3进行求整，可取消）：

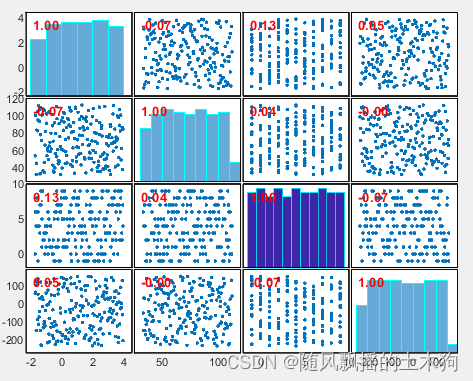
四、拉丁超立方抽样

ndim=4;%维度为4
minX=[-1.75, 32.4, -1, -234.2];%下限
maxX=[ 3.95, 112.56, 9, 156.37];%上限
popsize=200;%样本数
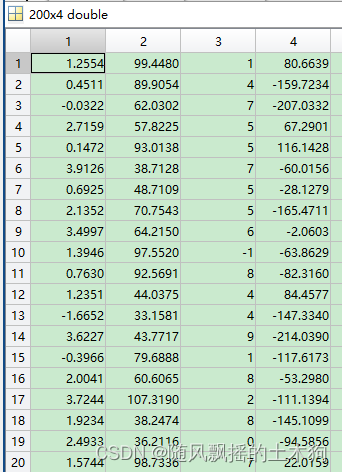
LHS抽样结果（其中对变量3进行求整，可取消）：

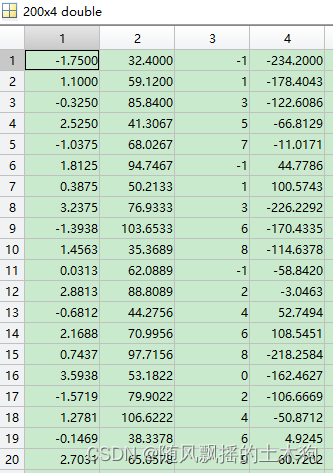
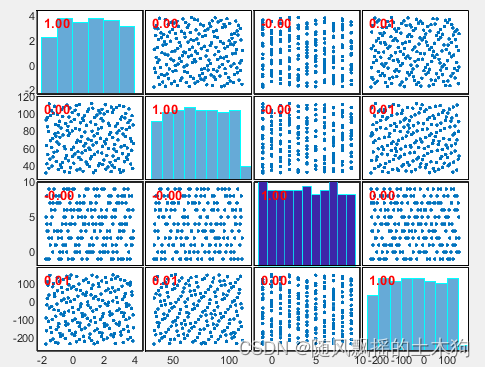
五、Halton抽样

ndim=4;%维度为4
minX=[-1.75, 32.4, -1, -234.2];%下限
maxX=[ 3.95, 112.56, 9, 156.37];%上限
popsize=200;%样本数
Halton抽样结果（其中对变量3进行求整，可取消）：

六、代码获取

后台私信回复“79期”和自动回复的指令即可获取下载链接。