SLAM中相机姿态估计算法推导基础数学总结

news2025/11/3 5:15:20

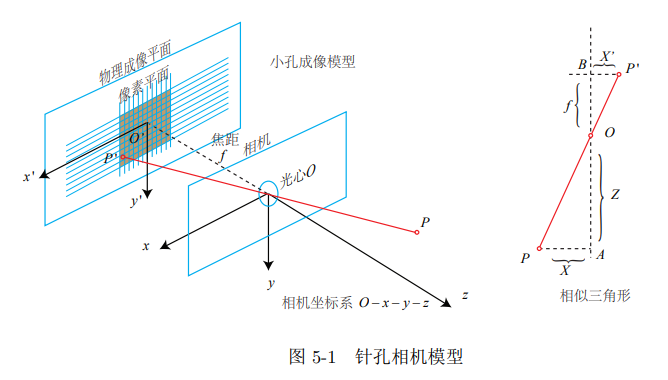
相机模型

基本模型

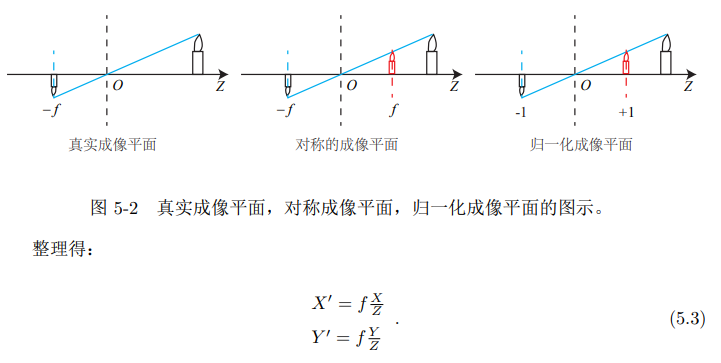
在这里插入图片描述
内参
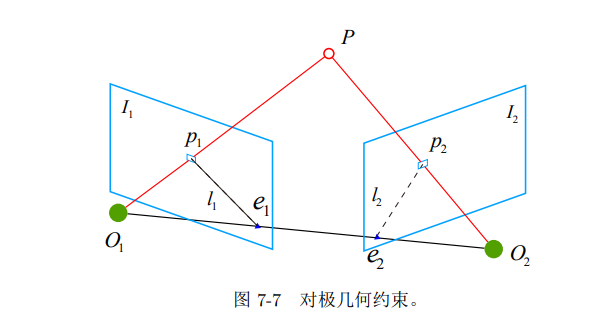
在这里插入图片描述
在这里插入图片描述
外参
在这里插入图片描述
在这里插入图片描述

对极几何

对极约束

在这里插入图片描述
在这里插入图片描述
外积符号
在这里插入图片描述
基础矩阵F和本质矩阵E
在这里插入图片描述
在这里插入图片描述
相机姿态估计问题分为如下两步:

在这里插入图片描述

本质矩阵

E = t ∧ R E=t^{\wedge}R E=t∧R因为 t ∧ t^{\wedge} t∧其实就是个3x3的反对称矩阵，所以 E E E也是一个3x3的矩阵

用八点法估计E
在这里插入图片描述
在这里插入图片描述

零空间矩阵的讲解

要通过E获得R和t就需要进行 E E E的奇异值(SVD)分解
在这里插入图片描述在这里插入图片描述
带入之后的看相机的正深度，就只有第一种情况满足

单应矩阵

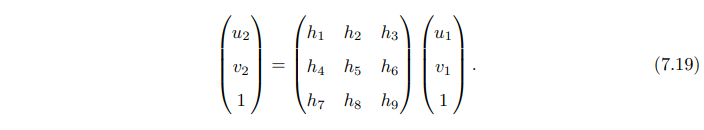
在这里插入图片描述
在这里插入图片描述

这个等式只有在非零因子情况下才成立，所以可以除以非零因子把 h 9 h_9 h9​变为0
在这里插入图片描述

三角测量

在这里插入图片描述在这里插入图片描述

3D-2D:PnP

直接线性变换

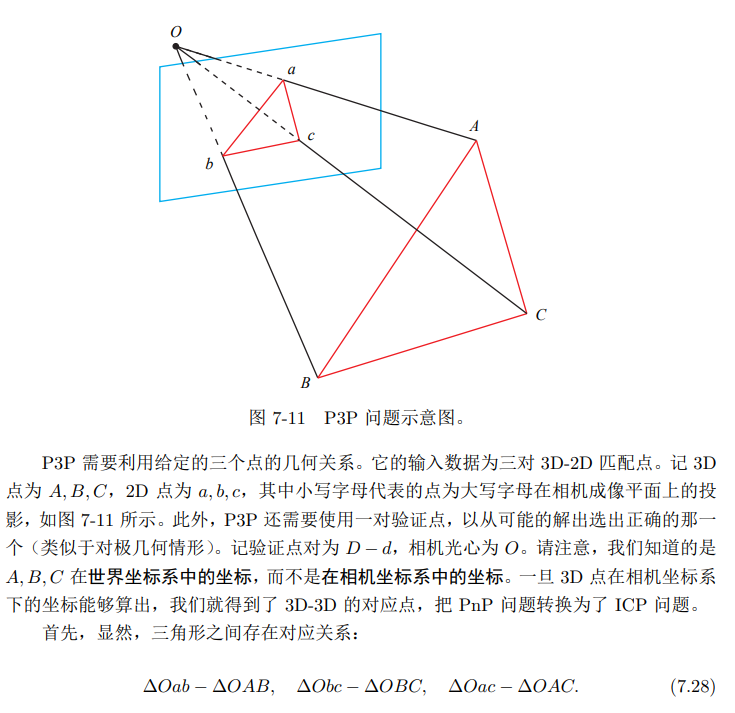
在这里插入图片描述

P3P

在这里插入图片描述
在这里插入图片描述
最后要求得未知量只有x,y,这是一个二元二次多项式方程，用吴消元法求解，最多得四个解，根据第四个点进行验证即可求得A，B,C 的3D坐标

Bundle Ajustment

在这里插入图片描述
这部分略显复杂，建议直接看视觉SLAM十四讲
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1112632.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

C语言求 n 阶勒让德多项式的值

C语言求 n 阶勒让德多项式的值

完整代码&#xff1a; // 用递归法求 n 阶勒让德多项式的值 // 递归公式为&#xff1a; // n0,P(n)(x)1 // n1,P(n)(x)x // n>1,P(n)(x)((2*n-1)*x - P(n-1)(x) - (n-1)*P(n-2)(x)) / n #include<stdio.h>double func(int n,int x){if (n0){return 1;}if (n1){return…
阅读更多...
爬虫基础 JS逆向

爬虫基础 JS逆向

爬虫核心 1. HTTP协议与WEB开发 1. 什么是请求头请求体&#xff0c;响应头响应体 2. URL地址包括什么 3. get请求和post请求到底是什么 4. Content-Type是什么 &#xff08;1&#xff09;简介 HTTP协议是Hyper Text Transfer Protocol&#xff08;超文本传输协议&#xff09;…
阅读更多...
行列转换：MySQL中的数据变形魔法

行列转换：MySQL中的数据变形魔法

行转列 使用CASE函数聚合函数 SELECTMAX(CASE WHEN salesperson John THEN sales_amount END) AS John_Sales,MAX(CASE WHEN salesperson Alice THEN sales_amount END) AS Alice_Sales FROM sales_data;列转行 使用UNIO连接每列数据 SELECT product_id,store1 store,sto…
阅读更多...
什么是SSL证书

什么是SSL证书

SSL 证书&#xff08;也称为公钥证书&#xff09;是安装在 Web 服务器上的加密文件&#xff0c;可帮助建立安全、加密的在线通信&#xff0c;SSL 证书有两个主要用途&#xff1a; 提供加密&#xff1a;当访问者的浏览器通过SSL连接到您的网站时&#xff0c;信息交换是加密的&a…
阅读更多...
Openssl数据安全传输平台003：Protobuf - 部署

Openssl数据安全传输平台003：Protobuf - 部署

文章目录 一、Windows环境二、Linux Centos环境三、protobuf测试3.1 新建.proto文件生成相应的类3.2 .proto生成相应的类的使用3.3 配置VS3.4 test代码 一、Windows环境 在windows下配置&#xff0c;无论protobuf是什么版本&#xff0c;IDE和编译器的版本都要保持一致。 比如…
阅读更多...
Day4力扣打卡

Day4力扣打卡

打卡记录 同积元组&#xff08;哈希表 排列组合&#xff09; 链接 思路&#xff1a;用哈希表将数组中出现的两不同数乘积依次记录&#xff0c;将出现两次以上的乘积组通过排列组合计算总情况个数。 class Solution { public:int tupleSameProduct(vector<int>& num…
阅读更多...
Redis设计与实现笔记 - 数据结构篇

Redis设计与实现笔记 - 数据结构篇

Redis设计与实现笔记 - 数据结构篇 相信在我们日常使用中&#xff0c;会经常跟 Redis 打交道。数据结构 String、Hash、List、Set 和 ZSet 都是常用的数据类型。对于使用场景&#xff0c;我们可以滔滔不绝地说很多&#xff0c;但是我们从来就没有关心过它们的底层实现&#xf…
阅读更多...
智慧矿山：煤流量检测AI算法——等级还是百分比显示，哪种更适合现场

智慧矿山：煤流量检测AI算法——等级还是百分比显示，哪种更适合现场

智慧矿山作为矿山工业的重要发展方向&#xff0c;AI算法的应用正逐渐改变传统的矿山生产方式。在智慧矿山中&#xff0c;煤流量检测是其中一项重要的任务。然而&#xff0c;在煤流量检测中&#xff0c;是采用等级显示还是百分比显示更适合现场呢&#xff1f; 煤流量检测作为煤矿…
阅读更多...
【试题022】C语言算数表达式例题

【试题022】C语言算数表达式例题

1.题目&#xff1a;设int a12&#xff0c;b10;&#xff0c;则表达式a%b/a*b的值为&#xff1f; 2.代码分析&#xff1a; #include <stdio.h> int main() {//设int a12&#xff0c;b10;&#xff0c;则表达式a%b/a*b的值为&#xff1f;int a 12,b 10;printf("%d\n…
阅读更多...
Python 面向对象进阶

Python 面向对象进阶

目录 1 面向对象三大特征介绍2 继承2.1 语法格式2.2 类成员的继承和重写2.3 查看类的继承层次结构 3 object根类3.1 dir()查看对象属性3.2 重写__str__()方法 4 多重继承5 MRO()6 super()获得父类定义7 多态8 特殊方法和运算符重载9 特殊属性10 对象的浅拷贝和深拷贝11 组合12 …
阅读更多...
CSP赛前复习总结

CSP赛前复习总结

文章目录 时空复杂度分析算法回顾基础算法贪心删数问题题目描述输入格式输出格式样例输入样例输出 贪心问题的具体应用双指针二分例题 分治 数据结构做题经历&#xff08;低级错误&#xff09;先从周考题说起FirstSecond 还有一两天就CSP了&#xff0c;特此为近期的复习进行总结…
阅读更多...
运机集团-001288 基本面分析（20231019）

运机集团-001288 基本面分析（20231019）

运机集团-001288 基本面分析 基本情况 公司名称&#xff1a;四川省自贡运输机械集团股份有限公司 A股简称&#xff1a;运机集团 成立日期&#xff1a;2003-09-28 上市日期&#xff1a;2021-11-01 所属行业&#xff1a;通用设备制造业 主营业务&#xff1a;以带式输送机为主的节…
阅读更多...
计算机操作系统-第十一天

计算机操作系统-第十一天

目录 1、进程的状态 创建态与就绪态 运行态 终止态 新建态 结束态 进程状态的转换 进程的组织方式 链接方式&#xff08;常见&#xff09; 索引方式&#xff08;少见&#xff09; 本节思维导图 1、进程的状态 创建态与就绪态 1、进程正在被创建时&#xff0c;处于…
阅读更多...
03、爬取资料---但是失败，仅作为记录

03、爬取资料---但是失败，仅作为记录

1、找网址 进入直播间&#xff0c;里面的用户被设置不对外查看。 如图&#xff0c;找url 2、伪装 user-agent 用户代理 cookie 用户登录后保留的信息 登录信息&#xff1a;找cookie 浏览器信息&#xff1a;找user-agent user-agent 用户代理 cookie 用户登录后保留的信…
阅读更多...
kubernetes集群编排

kubernetes集群编排

目录 k8s 集群部署 集群环境初始化 所有节点安装kubeadm 拉取集群所需镜像 集群初始化 安装flannel网络插件 设置kubectl命令补齐 k8s 集群部署 实验环境 主机名 ip 角色 k8s1&#xff08;上一章的docker1&#xff09; 192.168.81.10 reg.westos.org&#xff0c;harbor仓库…
阅读更多...
机器学习中参数优化调试方法

机器学习中参数优化调试方法

1 超参数优化 调参即超参数优化&#xff0c;是指从超参数空间中选择一组合适的超参数&#xff0c;以权衡好模型的偏差(bias)和方差(variance)&#xff0c;从而提高模型效果及性能。常用的调参方法有&#xff1a; 人工手动调参 网格/随机搜索(Grid / Random Search) 贝叶斯优…
阅读更多...
Kingbase备份与还原及表的约束(Kylin)

Kingbase备份与还原及表的约束(Kylin)

备份与还原 逻辑备份是对整个数据库好数据库中的部分对象利用逻辑备份工具导出数据到备份文件在需要数据恢复的情况下利用逻辑还原工具把备份文件恢复到数据库中 使用场景 逻辑备份主要用于数据库逻辑错误的恢复&#xff0c;恢复后对其他数据没有太大影响逻辑备份可用于在大…
阅读更多...
Java：ApacheHttpClient连接寿命(timeToLive)未配置问题分析

Java：ApacheHttpClient连接寿命(timeToLive)未配置问题分析

一、问题描述 若 Apache HttpClient 未设置 timeToLive&#xff0c;通过服务域名访问服务的实例并且服务域名解析出的 IP 发生变化时&#xff0c;在短时间内会有部分请求出现连接异常错误。 二、问题分析 Apache HttpClient 通过服务域名从连接池获取连接&#xff0c;当连接…
阅读更多...
IDEA中SpringBoot项目的yml多环境配置

IDEA中SpringBoot项目的yml多环境配置

SpringBoot的yml多环境配置 创建多个配置文件 application.yml #主配置文件 application-dev.yml #开发环境的配置 application-test.yml #测试环境的配置在application.yml中添加多环境配置属性 spring:profiles:active: profiles.active项目启动可能不会识别&#x…
阅读更多...
简单了解一下：Node的util工具模块

简单了解一下：Node的util工具模块

了解util模块&#xff0c;知道怎么使用util来格式化字符串&#xff0c;把对象转化为字符串&#xff0c;检查对象类型。 那么util模块有哪些方法呢&#xff1f;如下图所示&#xff1a; 常用的几个方法&#xff1a; 格式化输出字符串 util提供的格式化方法为&#xff1a;form…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023