手写一个PrattParser基本运算解析器3: 基于Swift的PrattParser的项目概述

news2025/7/14 20:40:07

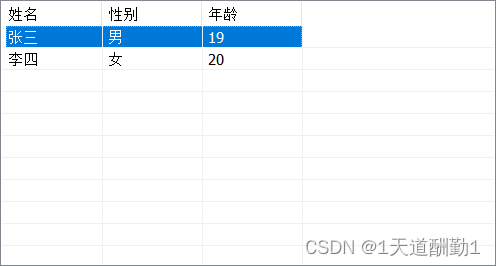
点击查看 基于Swift的PrattParser项目


PrattParser项目概述

前段时间一直想着手恶补 编译原理 的相关知识, 一开始打算直接读大学的 编译原理, 虽然内容丰富, 但是着实抽象难懂. 无意间看到B站的熊爷关于普拉特解析器相关内容, 感觉是一个非常好的切入点.所以就写了基于Swift版本的 PrattParser.

下面是我整理的项目中各个类以及其中函数的作用.

更加具体的请查看 PrattParser解释器项目类与函数


接下来, 我把整个项目UML图发出来, 大家可以借鉴查看.

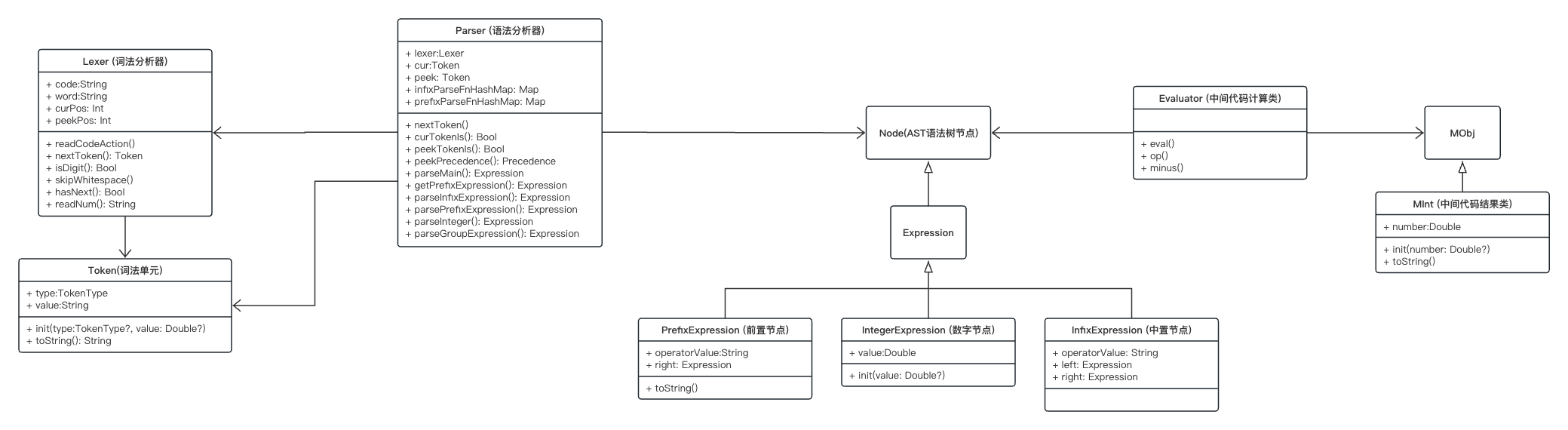
更加具体的请查看 PrattParser的Swift项目UML图


接下来, 我就以 词法分析 、语法分析 、 中间代码生成 三部分逐步来说明一下这个 基于Swift的PrattParser项目


词法分析

词法分析的核心类是 Lexer, 输入的原始代码字符串 code, 输出的是一组词法单元 Token.

在词法分析器 Lexer 中, 核心函数就是 nextToken, nextToken函数职责一共有两个职责.

  • 去除代码格式化的逻辑, 例如, 去除 空格 换行 等等. 这一步主要是通过调用 skipWhitespace() 函数实现的.

    public func skipWhitespace() {
    while (hasNext()) {
        if (word == " " || word == "\t" || word == "\n" || word == "\r")  {
            readCodeAction();
        } else {
            break
        }
    }
}

  • 读取数学符号与数字并且生成 词法单元Token

    switch(word) {
case "+" :
    token = PrattParser.Token(TokenType.PLUS, "+")
    break
case "-" :
    token = PrattParser.Token(TokenType.MINUS, "-")
    break
case "*" :
    token = PrattParser.Token(TokenType.ASTERISK, "*")
    break
case "/" :
    token = PrattParser.Token(TokenType.SLASH, "/")
    break
case "(" :
    token = PrattParser.Token(TokenType.LPAREN, "(")
    break
case ")" :
    token = PrattParser.Token(TokenType.RPAREN, ")")
    break
case "^" :
    token = PrattParser.Token(TokenType.HAT, "^")
    break
case nil :
    token = PrattParser.Token(TokenType.EOF, "")
    break
default:
    if (isDigit(word)) {
        let num: String = readNum();
        token = PrattParser.Token(TokenType.NUM, num);
        return token;
    } else {
        throw LexerError.lexerError(message: "Lexer error")
    }
}

生成词法单元函数 nextToken 的整体逻辑流程图如下所示. 基本涉及了词法分析器 Lexer 的所有函数.

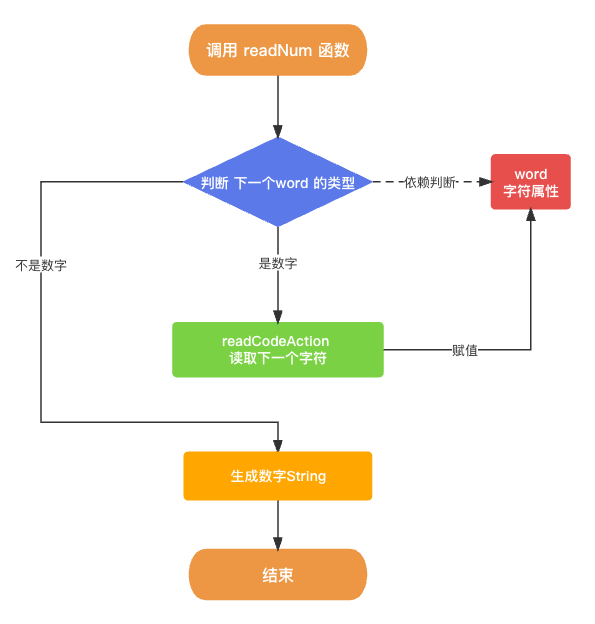
这里要补充的一点的就是由于数学符号大部分是单个字符, 例如 + - * / ( ), 这个读取直接生成即可. 但是数字可能是有多位的, 所以生成的过程需要通过循环一直查找. 在该项目中的代码实现中读取数字字符的逻辑代码主要存在于 readNum 函数中.

public func readNum() -> String {
    var num: String = ""
    while (isDigit(word)) {
        num += word ?? ""
        readCodeAction()
    }
    return num;
}

生成数字函数 readNum 的整体逻辑流程图如下所示.

在该项目中, 词法分析器Lexer 的外部驱动力是 语法分析器Parser, 也就是说语法分析器Parser一直在调用 Lexer 的 nextToken 函数从而不断地生成词法单元 Token.


语法分析

在 词法分析 模块, 我们了解到了 词法分析器Lexer 会为 语法分析器Parser 提供源源不断生成的词法单元 Token.

语法分析器Parser 则会这些词法单元 Token根据 符号的优先级 生成一颗 AST语法树.

在 语法分析器Parser 生成 AST语法树 的过程中, 其入口函数是 parseMain(), 核心函数是 parseExpression(), 具体代码如下所示.

func parseExpression(_ precedence: Precedence) -> Expression? {
    let funcName: String?  = prefixParseFnHashMap[cur?.type ?? TokenType.None];
    if (funcName == nil) {
        print("未找到AST节点构建函数名称")
        return nil
    }
    // 生成前置节点, 获取左节点
    var leftExpression: Expression? = getPrefixExpression(funcName);
    
    // 能递归的原因 判断下一个词法单元是否是EOF, 判断下一个词法单元的优先级是否大于当前的优先级
    while (!peekTokenIs(TokenType.EOF) && precedence.rawValue < peekPrecedence()?.rawValue ?? 0) {
        let infixParseFnName: String?  = infixParseFnHashMap[peek?.type ?? TokenType.None];
        if (infixParseFnName == nil) {
            print("未找到AST节点构建函数名称")
            return leftExpression;
        }
        //读取下一个词法单元
        nextToken();
        // 生成中置节点, 更新AST语法树
        leftExpression = parseInfixExpression(leftExpression);
    }
    return leftExpression
}

由于递归过程比较复杂, 我整理了一下整体的逻辑流程图.

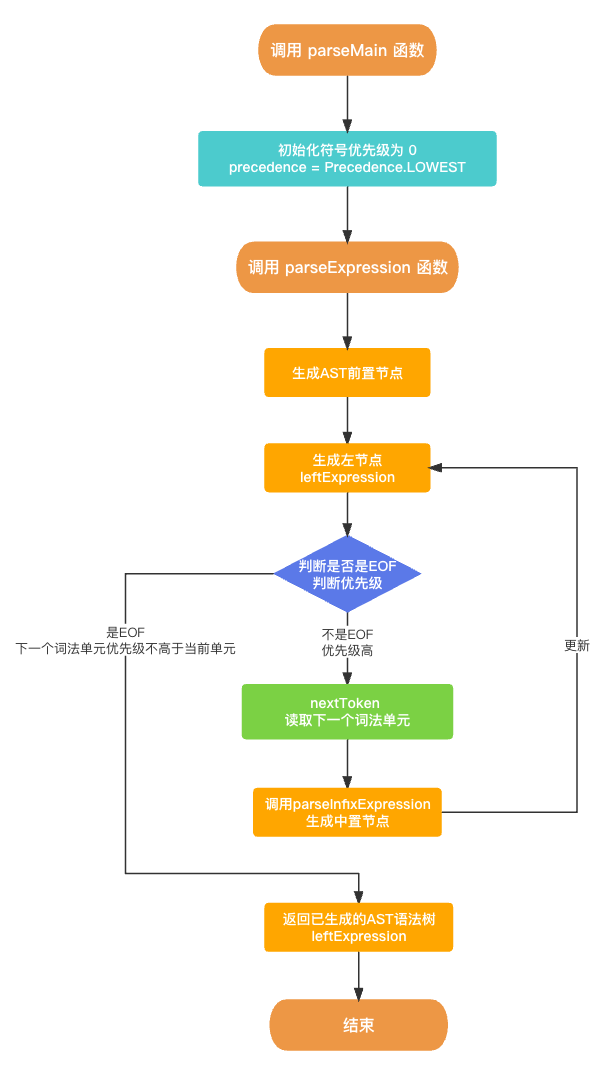
当我们看到上一个图的时候, 我们会诧异, 说好的递归过程在哪呢? 其实递归过程主要隐藏在生成中置节点函数 parseInfixExpression() 中, 由于 parseExpression() → parseInfixExpression() → parseExpression() → .... 的调用关系会最终产生递归效果.

在中置节点生成函数parseInfixExpression中, 右节点的生成依然会依赖 parseExpression(), 这也就递归产生的驱动力.

// 中置节点生成函数
func parseInfixExpression(_ left: Expression?) -> Expression? {
    let infixExpression = InfixExpression();
    infixExpression.left = left;
    infixExpression.operatorValue = cur?.value;
    let precedence: Precedence = Precedence.getPrecedence(cur?.type);
    nextToken();
    // 右节点的生成是递归产生的驱动力
    infixExpression.right = parseExpression(precedence);
    return infixExpression
}

中置节点生成函数parseInfixExpression的逻辑流程图如下所示.


粗略的说了大致的流程, 接下来, 我们就详情的说一下具体的执行流程.

具体的以 1 + 4 - 3 和 1 + 2 * 3 两个数学运算为示例.


1 + 4 - 3 的AST语法树构建过程

强烈建议大家一边项目断点, 一边对照该模块的流程!!!

  • 整体还是以 parseMain() 为入口, 初始过程中会传入一个最低的优先级(Precedence.LOWEST)用于驱动整个AST语法树的构建. 当然了, 这时候词法单元读取模块也已经准备就绪了.

    // 构建AST树主入口
public func parseMain() -> Expression? {
    return parseExpression(Precedence.LOWEST);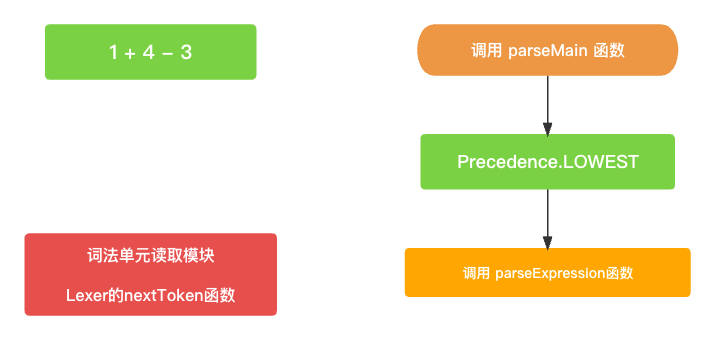
}

  • 通过 parseMain 函数进入的 parseExpression() 函数中, 首先找的就是前置节点, 通过 词法单元读取模块 获取到第一个词法单元 1. 并且生成根据 前置节点的类型 生成 数字类型的AST前置节点. getPrefixExpression 就不过多叙述了, 比较简单.

    let funcName: String?  = prefixParseFnHashMap[cur?.type ?? TokenType.None];
if (funcName == nil) {
    print("未找到AST节点构建函数名称")
    return nil
}
// 获取左节点
var leftExpression: Expression? = getPrefixExpression(funcName);

    func getPrefixExpression(_ funcName: String?) -> Expression? {
    switch(funcName) {
    case "parseInteger" :
        return parseInteger()
    case "parsePrefixExpression":
        return parsePrefixExpression()
    case "parseGroupExpression":
        return parseGroupExpression()
    default:
        return nil
    }
}

    func parseInteger() -> Expression? {
    let number = Double(cur?.value ?? "0")
    let integerExpression = IntegerExpression(value: number)
    return integerExpression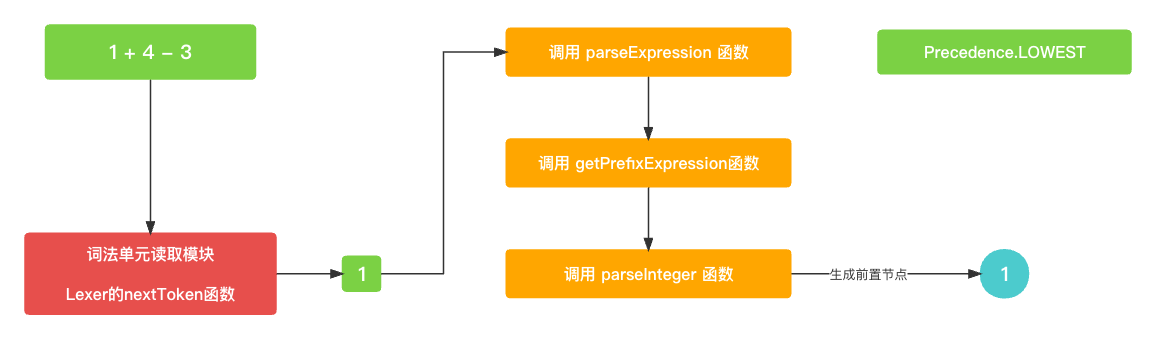
}

  • 紧接着就是去找到中置节点, 这时候通过peekPrecedence() 知道下一个词法单元为 +, 优先级较高, 满足优先级条件. 进入递归循环. 然后nextToken()读取下一个词法单元 +, 然后通过调用 parseInfixExpression() 尝试生成AST中的中置节点.

    while (!peekTokenIs(TokenType.EOF) && precedence.rawValue < peekPrecedence()?.rawValue ?? 0) {
    let infixParseFnName: String?  = infixParseFnHashMap[peek?.type ?? TokenType.None];
    if (infixParseFnName == nil) {
        print("未找到AST节点构建函数名称")
        return leftExpression;
    }
    nextToken();
    leftExpression = parseInfixExpression(leftExpression);
}

  • 在中置节点生成函数 parseInfixExpression() 中, 由于当前的词法单元为 + , 左节点为前置节点 1, 我们可以直接构建出这一部分的AST语法树.

    let infixExpression = InfixExpression();
infixExpression.left = left;
infixExpression.operatorValue = cur?.value;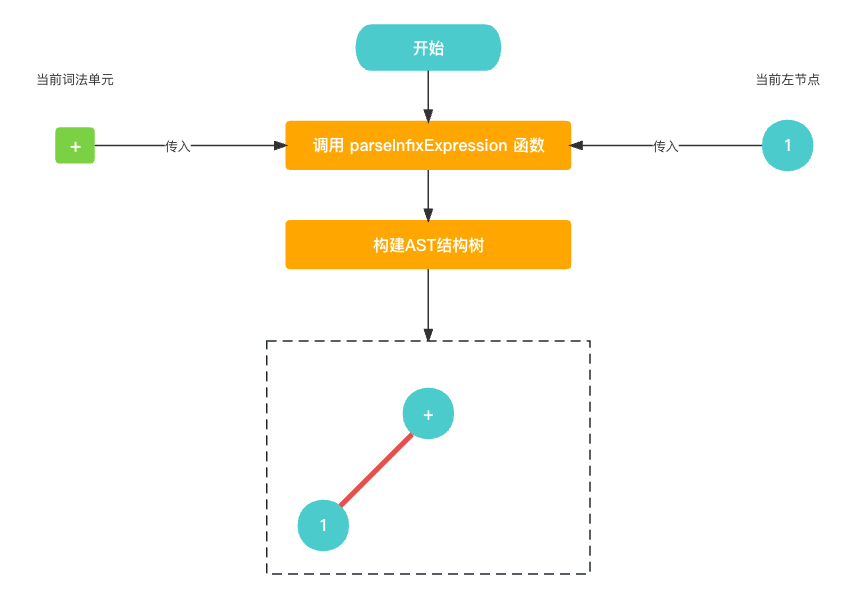

  • 构建了中置节点的值和左节点, 我们尝试用 parseExpression() 递归的形式找到 +的中置节点 的右节点, 我们需要先读取当前 + 的优先级(Precedence.SUM), 然后读取下一个节点.

    let precedence: Precedence = Precedence.getPrecedence(cur?.type);
nextToken();
infixExpression.right = parseExpression(precedence);

  • 在 parseExpression() 寻找 +的中置节点 的右节点, 首先, 就是获取 数字词法单元4 生成前置节点, 然后往后读取, 发现是 符号词法单元- 优先级与 当前 符号词法单元+ 的优先级相同, 所以就不进入while循环, 故+的中置节点 的右节点是 前置节点4.

    // 参数优先级为 Precedence.SUM
func parseExpression(_ precedence: Precedence) -> Expression? {
    let funcName: String?  = prefixParseFnHashMap[cur?.type ?? TokenType.None];
    if (funcName == nil) {
        print("未找到AST节点构建函数名称")
        return nil
    }
    // 获取左节点, 生成 数字前置节点 4
    var leftExpression: Expression? = getPrefixExpression(funcName);
    
    //  - 与 + 的优先级相同不进入while循环
    while (!peekTokenIs(TokenType.EOF) && precedence.rawValue < peekPrecedence()?.rawValue ?? 0) {
        let infixParseFnName: String?  = infixParseFnHashMap[peek?.type ?? TokenType.None];
        if (infixParseFnName == nil) {
            print("未找到AST节点构建函数名称")
            return leftExpression;
        }
        nextToken();
        leftExpression = parseInfixExpression(leftExpression);
    }
    // 返回 数字前置节点 4
    return leftExpression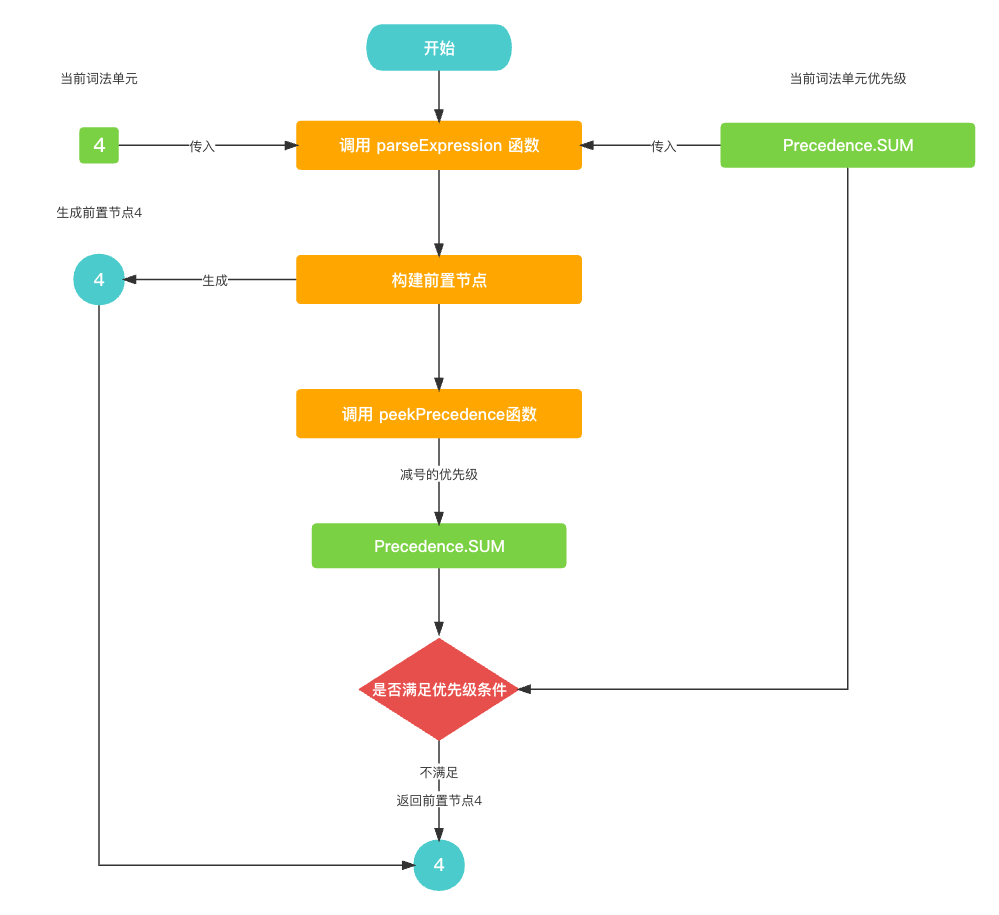
}

  • 这时候, 对于 中置节点+号 的AST语法树就构建完成了, 如图所示.

  • 然后外部又一次进行while循环, 这次找到的是 ➖ 号, 然后把 中置节点+号 的AST语法树 整体作为➖中置节点的左节点传入.

    // 这时候再次进入 减号➖ 的循环中
while (!peekTokenIs(TokenType.EOF) && precedence.rawValue < peekPrecedence()?.rawValue ?? 0) {
    let infixParseFnName: String?  = infixParseFnHashMap[peek?.type ?? TokenType.None];
    if (infixParseFnName == nil) {
        print("未找到AST节点构建函数名称")
        return leftExpression;
    }
    // 读取词法单元减号➖
    nextToken();
    // 这里的leftExpression是 加号➕ 的AST语法树
    //   +
    //  ╱ ╲
    // 1   4
    leftExpression = parseInfixExpression(leftExpression);
}

  • 在 ➖ 号的中置节点 构建过程中, 中置节点+号 的AST语法树 作为其左节点, - 作为其值, 右节点继续通过parseExpression()寻找.

    let infixExpression = InfixExpression();
// 这里的left是 加号➕ 的AST语法树
//   +
//  ╱ ╲
// 1   4
infixExpression.left = left;
infixExpression.operatorValue = cur?.value;

  • 和 中置节点+号 寻找右节点的逻辑是一样. 我们继续尝试用 parseExpression() 递归的形式找到 -的中置节点 的右节点, 我们需要先读取当前 - 的优先级(Precedence.SUM), 然后读取下一个节点.

    let precedence: Precedence = Precedence.getPrecedence(cur?.type);
nextToken();
infixExpression.right = parseExpression(precedence);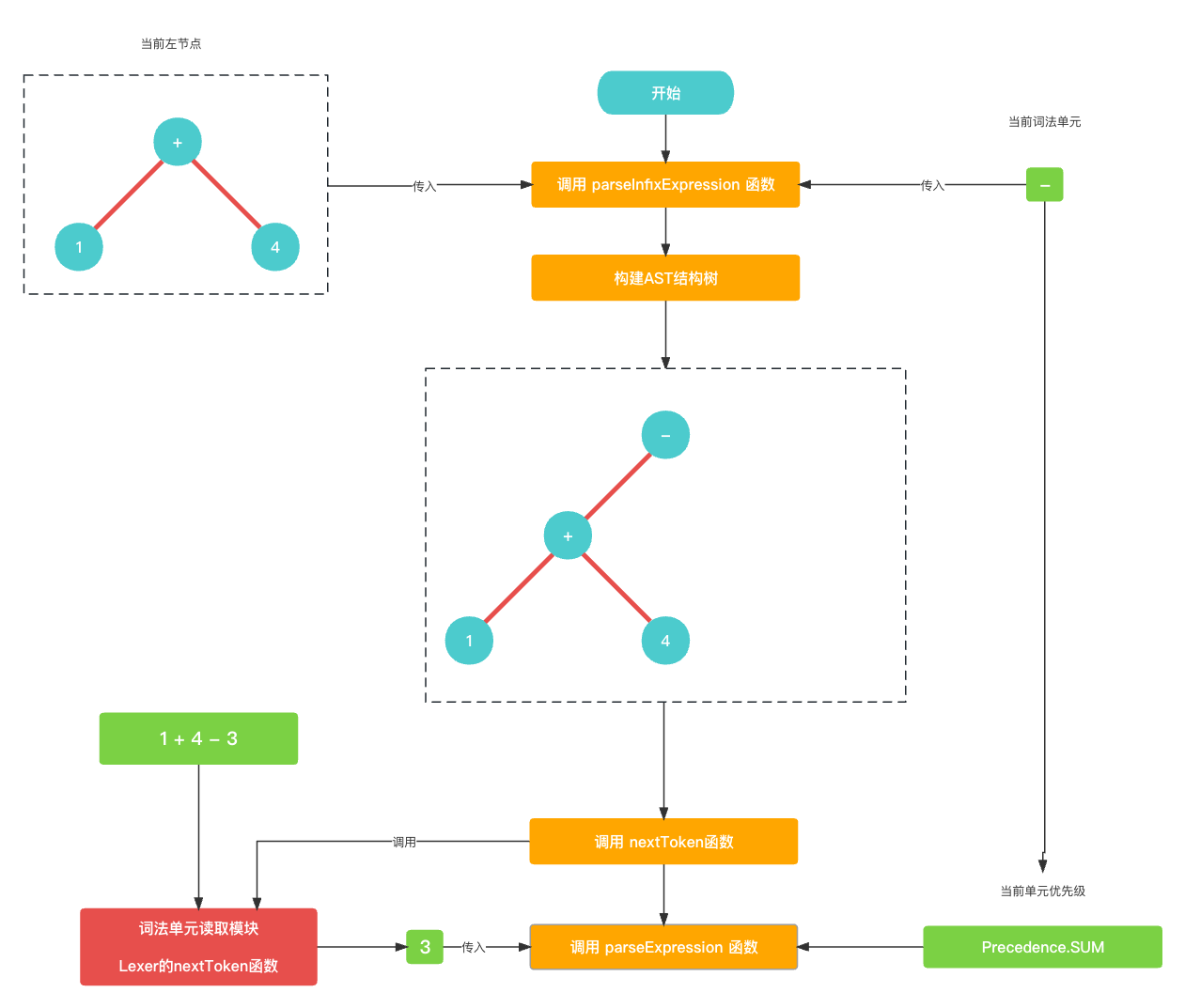

  • 这次在 parseExpression() 就很简单了, 我们先构建了前置节点3 然后往后查找过程发现是结束词法单元EOF, 我们直接返回 前置节点3 即可.

    func parseExpression(_ precedence: Precedence) -> Expression? {
    let funcName: String?  = prefixParseFnHashMap[cur?.type ?? TokenType.None];
    if (funcName == nil) {
        print("未找到AST节点构建函数名称")
        return nil
    }
    // 构建 前置节点3
    var leftExpression: Expression? = getPrefixExpression(funcName);
    
    // peekToken == EOF 不满足while循环条件
    while (!peekTokenIs(TokenType.EOF) && precedence.rawValue < peekPrecedence()?.rawValue ?? 0) {
        let infixParseFnName: String?  = infixParseFnHashMap[peek?.type ?? TokenType.None];
        if (infixParseFnName == nil) {
            print("未找到AST节点构建函数名称")
            return leftExpression;
        }
        nextToken();
        leftExpression = parseInfixExpression(leftExpression);
    }
    // 返回 前置节点3
    return leftExpression
}

  • 返回了右节点之后, 我们就直接构建 ➖减号的AST语法树, 这里看一下整体的构建过程.

  • ➖减号的AST语法树 然后再次返回整体的循环, 发现当前的词法节点以及全部循环完成了, 所以就跳出了while循环, 返回最终的AST语法树. 这里就把整理的流程贴图如下所示.

  • 所以1 + 4 - 3 形成的AST语法树是这样的. 如下图所示.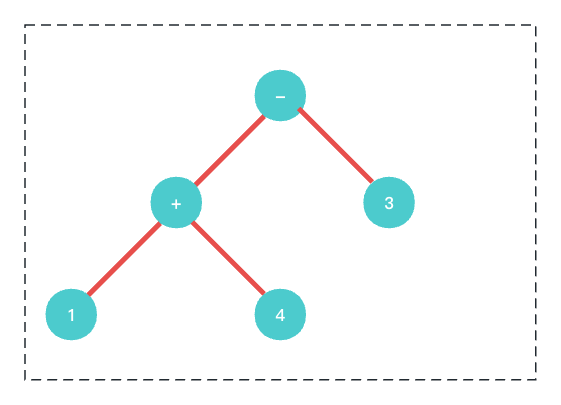


1 + 2 * 3 的AST语法树构建过程

相比于 1 + 4 - 3 的最终结果来说, 1 + 2 * 3 其中 乘法* 一定要比 加法+ 优先级高. 最终应该是这样的 1 + (2 * 3) . 也就是我们预想的AST语法树应该如下所示.

接下来, 我们就一起看一下 1 + 2 * 3 的AST语法树构建逻辑.

  • 对于 1 + 2 * 3 一直到加法的中置节点寻找右节点之前的逻辑都是与先前一样的. 这里直接贴图了, 就不过多叙述代码了.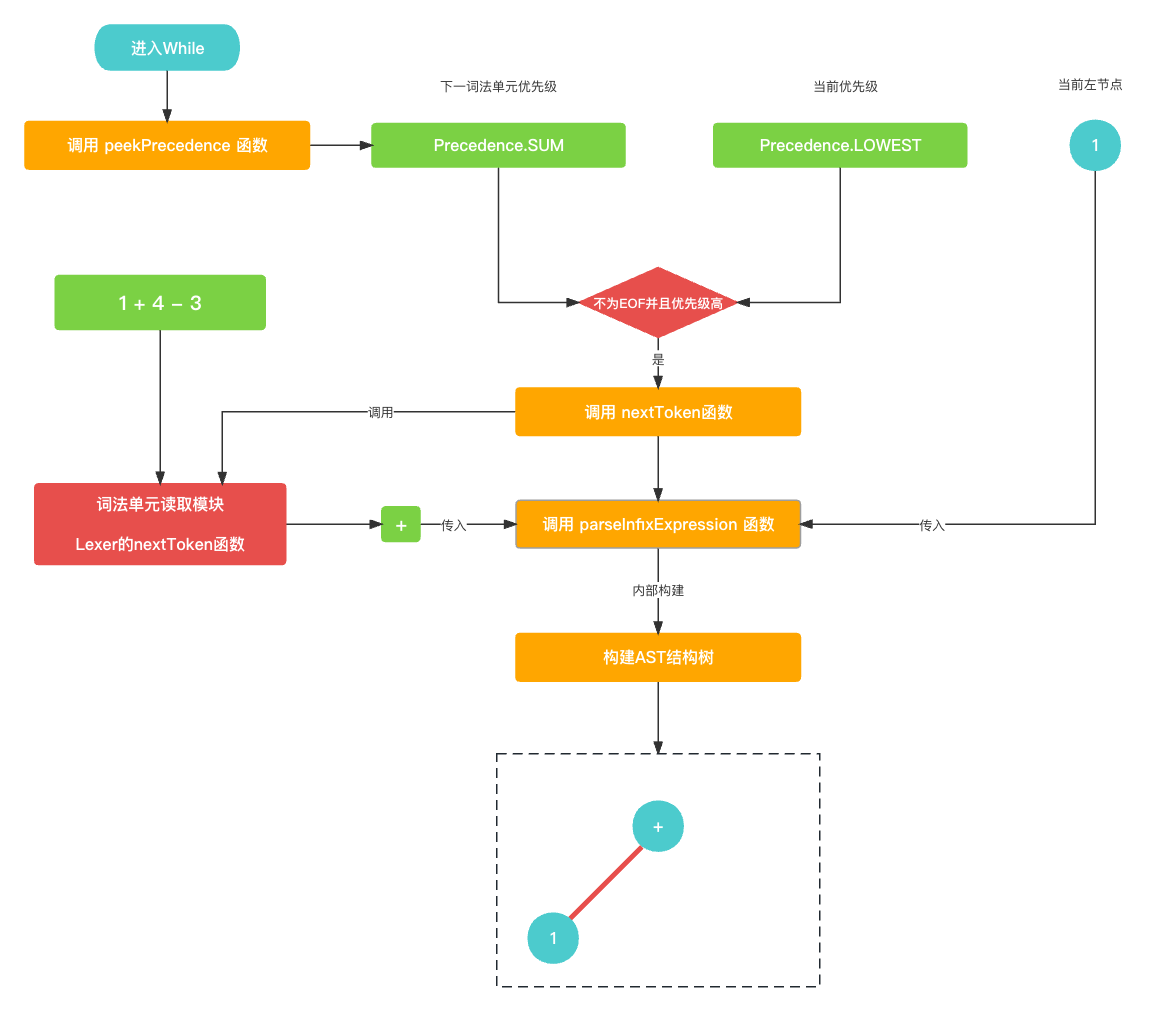

  • 接下来, 对于 中置节点加号+ 需要通过 parseExpression() 去寻找它自身的右节点. 这时候准备工作也要做好, 读取下一个词法单元2, 获取当前加号的优先级(Precedence.SUM).

    // 当前加号的优先级为 Precedence.SUM
let precedence: Precedence = Precedence.getPrecedence(cur?.type);
// 下一个词法单元为 词法单元2
nextToken();
// 寻找 中置节点加号+ 的 右节点
infixExpression.right = parseExpression(precedence);

  • 然后, 在 parseExpression() 就是先构建 前置节点2, 然后查看后一个词法单元, 发现是 乘法符号*, 乘法符号的优先级(Precedence.PRODUCT) 要比 加法符号的优先级(Precedence.SUM) 要高, 所以进入while循环中. 继续构建关于 中置节点乘法* 的相关AST语法树.

    // 当前优先级是 Precedence.SUM, 当前Token是 2
func parseExpression(_ precedence: Precedence) -> Expression? {
    let funcName: String?  = prefixParseFnHashMap[cur?.type ?? TokenType.None];
    if (funcName == nil) {
        print("未找到AST节点构建函数名称")
        return nil
    }
    // 构建左节点 前置节点2
    var leftExpression: Expression? = getPrefixExpression(funcName);
    
    // 乘法符号的优先级比当前加号优先级高, 正常进入while循环
    while (!peekTokenIs(TokenType.EOF) && precedence.rawValue < peekPrecedence()?.rawValue ?? 0) {
        let infixParseFnName: String?  = infixParseFnHashMap[peek?.type ?? TokenType.None];
        if (infixParseFnName == nil) {
            print("未找到AST节点构建函数名称")
            return leftExpression;
        }
        // 读取下一个词法单元 乘法符号*
        nextToken();
        // 生成乘法符号的中置节点并且更新leftExpression
        leftExpression = parseInfixExpression(leftExpression);
    }
    return leftExpression
}

    let infixExpression = InfixExpression();
infixExpression.left = left;
infixExpression.operatorValue = cur?.value;
// 当前的乘法符号 的AST语法树
//   *
//  ╱ ╲
// 2   ?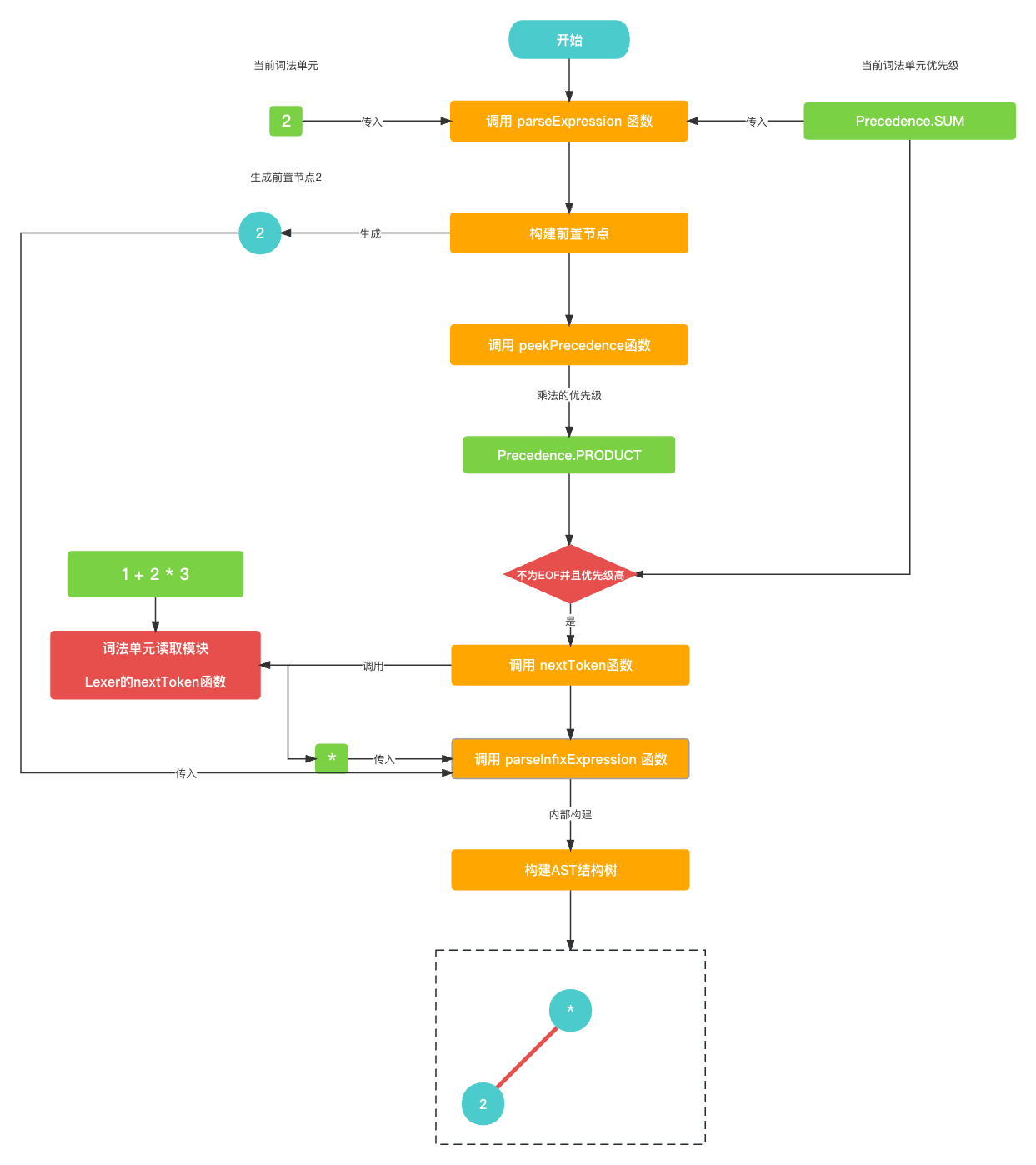

  • 紧接着, 就是寻找乘法AST语法树的右节点, 仍然是通过 parseExpression() 函数, 传入的Token则是 词法单元3, 乘法符号的优先级为 Precedence.PRODUCT,

    // 乘法符号的优先级为 Precedence.PRODUCT
let precedence: Precedence = Precedence.getPrecedence(cur?.type);
// 读取词法单元3
nextToken();
infixExpression.right = parseExpression(precedence);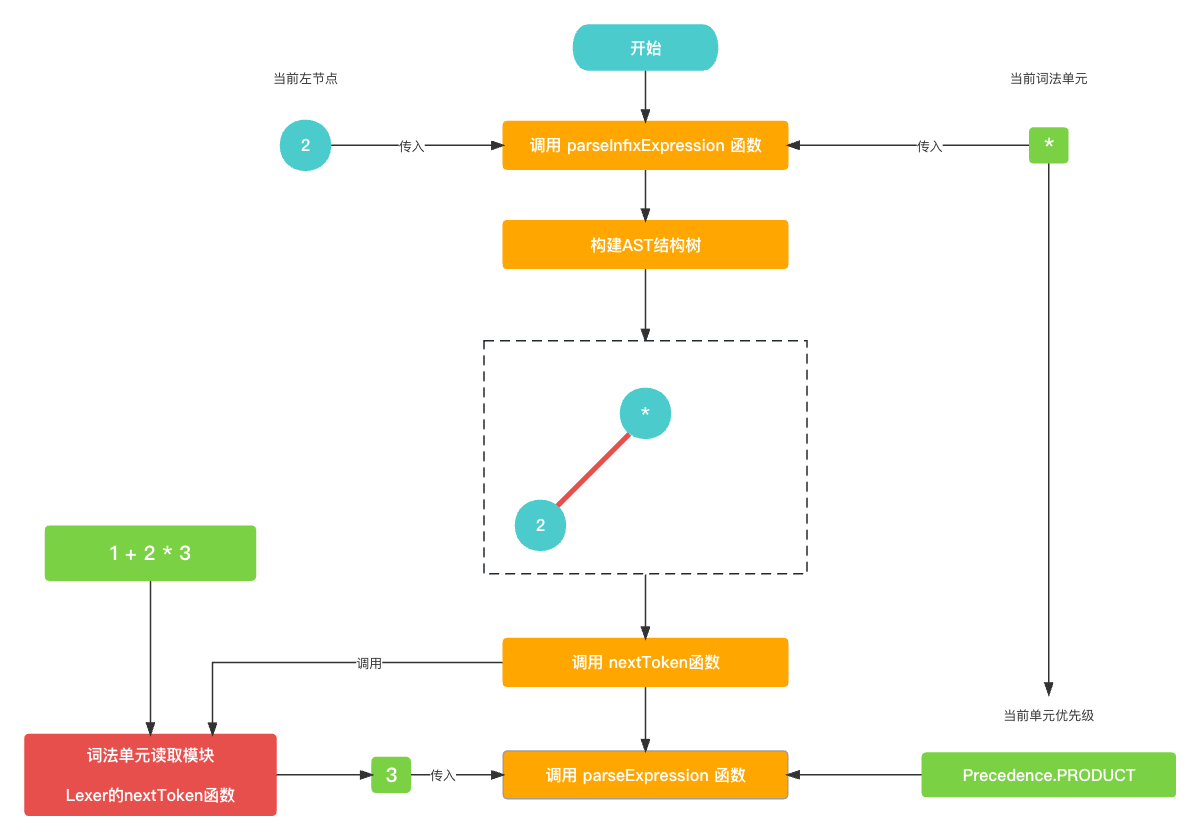

  • 在这次乘法符号寻找右节点的 parseExpression() 中, 首先构建了 前置节点3, 由于看到下一个节点是 结束词法单元EOF, 所以不进入循环, 直接返回 前置节点3.

    func parseExpression(_ precedence: Precedence) -> Expression? {
    let funcName: String?  = prefixParseFnHashMap[cur?.type ?? TokenType.None];
    if (funcName == nil) {
        print("未找到AST节点构建函数名称")
        return nil
    }
    // 构建 前置节点3
    var leftExpression: Expression? = getPrefixExpression(funcName);
    
    // peekToken == EOF 不满足while循环条件
    while (!peekTokenIs(TokenType.EOF) && precedence.rawValue < peekPrecedence()?.rawValue ?? 0) {
        let infixParseFnName: String?  = infixParseFnHashMap[peek?.type ?? TokenType.None];
        if (infixParseFnName == nil) {
            print("未找到AST节点构建函数名称")
            return leftExpression;
        }
        nextToken();
        leftExpression = parseInfixExpression(leftExpression);
    }
    // 返回 前置节点3
    return leftExpression
}

  • 这时候也就构建完成了乘法的AST语法树部分了. 我们一起看一下整体的乘法符号的AST语法树构建过程.

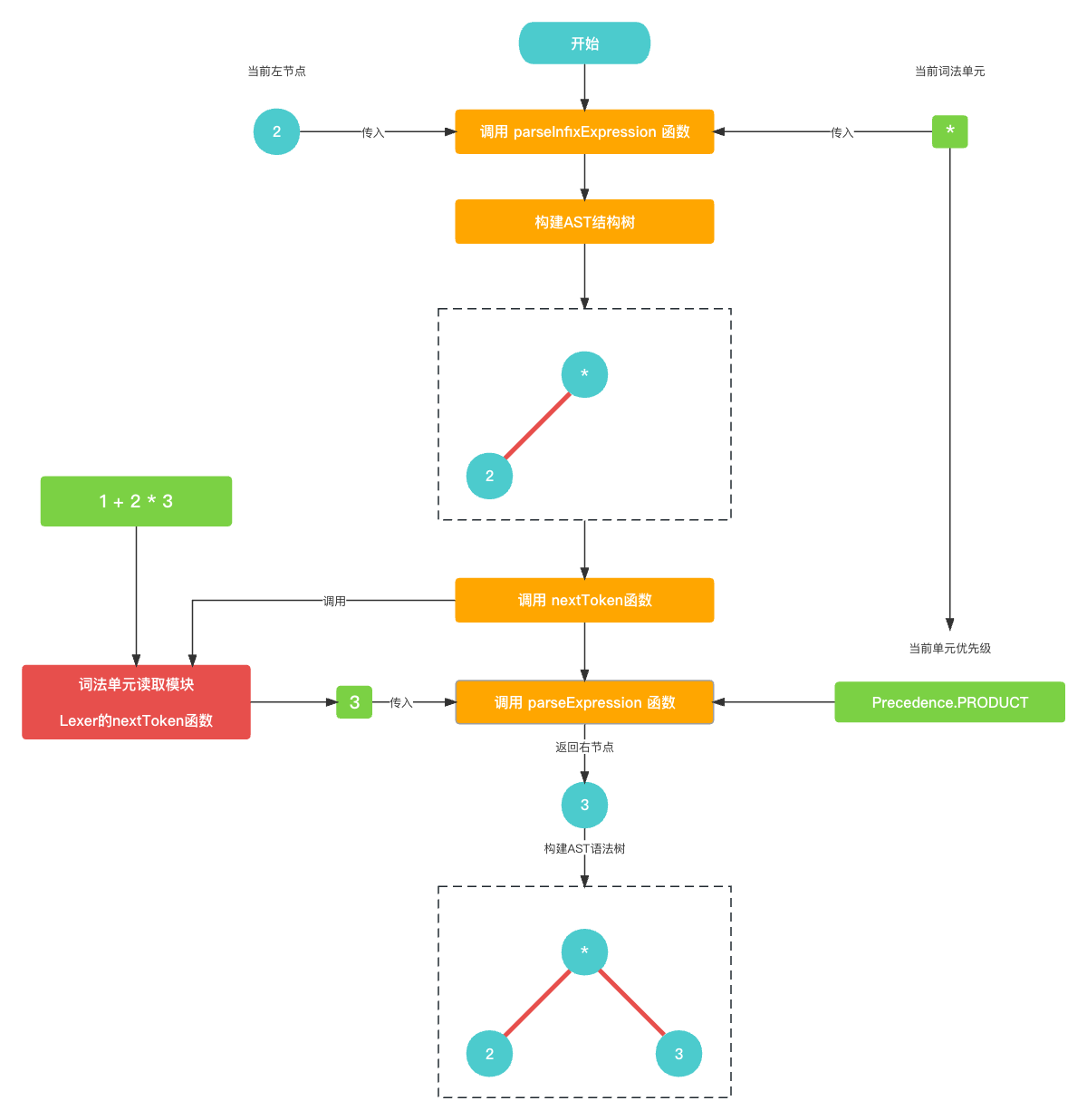
  • 由于已经遍历到了最后(遇到了EOF), 紧接着就跳出了 加法符号寻找右节点的parseExpression()过程中的while循环. 并把 乘法符号的AST语法树作为 加法符号的右节点进行了添加.

    // 这里是加法符号寻找右节点的递归方法
// 当前优先级是 Precedence.SUM, 当前Token是 2
func parseExpression(_ precedence: Precedence) -> Expression? {
    let funcName: String?  = prefixParseFnHashMap[cur?.type ?? TokenType.None];
    if (funcName == nil) {
        print("未找到AST节点构建函数名称")
        return nil
    }
    // 构建左节点 前置节点2
    var leftExpression: Expression? = getPrefixExpression(funcName);
    
    // 乘法符号的优先级比当前加号优先级高, 正常进入while循环
    while (!peekTokenIs(TokenType.EOF) && precedence.rawValue < peekPrecedence()?.rawValue ?? 0) {
        let infixParseFnName: String?  = infixParseFnHashMap[peek?.type ?? TokenType.None];
        if (infixParseFnName == nil) {
            print("未找到AST节点构建函数名称")
            return leftExpression;
        }
        // 读取下一个词法单元 乘法符号*
        nextToken();
        // 生成乘法符号的中置节点并且更新leftExpression
        leftExpression = parseInfixExpression(leftExpression);
    }

    // 最终 leftExpression 是乘法符号的AST语法树
    //   *
    //  ╱ ╲
    // 2   3
    return leftExpression
}

    上述代码就是下图中 红色的parseExpression()的内部过程.

  • 最后返回初始那一层 由 parseMain() 进入的 parseExpression() 过程, 也是已经遍历到了最后(遇到了EOF), 跳出循环, 返回最终的AST语法树.

    // 这里是由 `parseMain()` 进入的 `parseExpression()`
func parseExpression(_ precedence: Precedence) -> Expression? {
    let funcName: String?  = prefixParseFnHashMap[cur?.type ?? TokenType.None];
    if (funcName == nil) {
        print("未找到AST节点构建函数名称")
        return nil
    }
    // 构建左节点 前置节点1
    var leftExpression: Expression? = getPrefixExpression(funcName);
    
    // 构建了加法的AST语法树之后, 就退出了循环
    while (!peekTokenIs(TokenType.EOF) && precedence.rawValue < peekPrecedence()?.rawValue ?? 0) {
        let infixParseFnName: String?  = infixParseFnHashMap[peek?.type ?? TokenType.None];
        if (infixParseFnName == nil) {
            print("未找到AST节点构建函数名称")
            return leftExpression;
        }
        nextToken();
        leftExpression = parseInfixExpression(leftExpression);
    }

    // 最终 leftExpression 是加法符号的AST语法树
    //   +
    //  ╱ ╲
    // 1   *
    //    ╱ ╲
    //   2   3
    return leftExpression
}

  • 这样我们对于数学表达式的 1 + 2 * 3 的 AST语法树构建过程就有整体的了解,最终输出的AST语法树如下所示.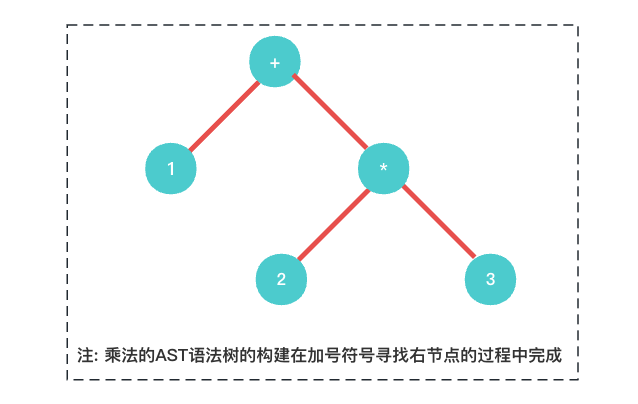


中间代码生成与验证

对于上面的 1 + 4 - 3 和 1 + 2 * 3 的两个示例, 我们对PrattParser构建AST语法树的过程有了大体的了解.

接下来就是中间代码生成过程(其实不太准确, 大体模拟吧~), 我们会直接输入一个结果对象(MInt), 模拟中间代码的生成.

中间代码生成是由 Evaluator 来实现的, 其主要作用就是解析AST语法树, 生成中间代码结果对象(MInt). 这部分也是很简单, 主要是通过 eval() 函数来递归解析AST语法树, 然后通过 op() 函数进行各种数学计算. 整体的计算也是由递归完成的.

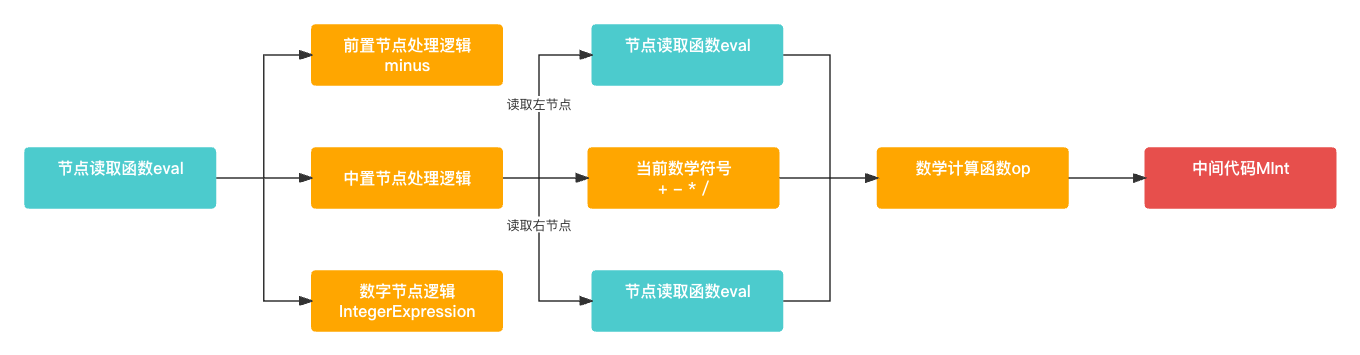
  • eval() 函数中 主要有三个逻辑分支, 一个是数字的前置节点 一个是符号的前置节点, 最后一个是中置节点. 数字的前置节点 和 中置节点 没有什么好说的, 符号的前置节点 主要应对于第一个前置节点带符号的情况例如 -1 和 +349 等等.

    public static func eval(_ node: Node?) -> MObj? {
    if let nodeValue = node as? IntegerExpression {
        // 纯数字节点逻辑
        return MInt(nodeValue.value)
    } else if let nodeValue = node as? PrefixExpression {
        // 带符号的数字节点逻辑
        if (nodeValue.operatorValue == "-") {
            return minus(node);
        } else if (nodeValue.operatorValue == "+") {
            return eval(nodeValue.right);
        }
    } else if let nodeValue = node as? InfixExpression {
        // 中置节点逻辑
        let left = eval(nodeValue.left);
        let right = eval(nodeValue.right);
        return op(left, right, nodeValue.operatorValue);
    }
    return nil;
}

  • op() 就是根据符号进行不同的数学运算, 整体逻辑比较简单, 这里就不过多叙述了.

    public static func op(_ left: MObj?, _ right: MObj?, _ operatorValue: String?) -> MObj? {
    if let leftValue = left as? MInt,
       let rightValue = right as? MInt {
        switch(operatorValue) {
        case "+" :
            return MInt(leftValue.number + rightValue.number)
        case "-" :
            return MInt(leftValue.number - rightValue.number)
        case "*" :
            return MInt(leftValue.number * rightValue.number)
        case "/" :
            return MInt(leftValue.number / rightValue.number)
        case "^" :
            return MInt(pow(leftValue.number, rightValue.number))
        default:
            return nil;
        }
    }
    return nil;
}

  • minus() 函数主要是用来处理带符号的前置节点情况. 整体逻辑也比较简单, 这里就不过多叙述了.

    public static func minus(_ node: Node?) -> MObj? {
    if let nodeValue = node as? PrefixExpression {
        let m : MObj? = eval(nodeValue.right);
        if let mValue = m as? MInt {
            if (nodeValue.operatorValue == "-") {
                mValue.number = -mValue.number
            }
            return mValue;
        }
    }
    return nil;
}

最后, 我们就能看到最终的输出结果.

var code = "1+2*3"

var lexer: Lexer! = Lexer(code: code)

var parser: Parser! = Parser(lexer)

var expression: Expression? = parser.parseMain()

if let intObj = Evaluator.eval(expression) as? MInt {
    print(intObj.toString())
}


总结

通过这篇博客详细大家对 PrattParser解析器的前端工作有个大体的了解了. 希望看这篇博客是可以一边断点项目, 一边查看, 主要是递归过程比较绕, 希望有耐心看完.


点击查看 基于Swift的PrattParser项目


本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1103086.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

试着写几个opencv的程序

试着写几个opencv的程序

一、认识opencv OpenCV&#xff08;Open Source Computer Vision Library&#xff09;是一个开源计算机视觉库&#xff0c;旨在提供丰富的图像处理和计算机视觉功能&#xff0c;以帮助开发者构建视觉应用程序。OpenCV最初由英特尔开发&#xff0c;现在由社区维护和支持。它支持…
阅读更多...
【Javascript保姆级教程】显示类型转换和隐式类型转换

【Javascript保姆级教程】显示类型转换和隐式类型转换

文章目录 前言一、显式类型转换1.1 字符串转换1.2 数字转换1.3 布尔值转换 二、隐式类型转换2.1 数字与字符串相加2.2 布尔值与数字相乘 总结 前言 JavaScript是一种灵活的动态类型语言&#xff0c;这意味着变量的数据类型可以在运行时自动转换&#xff0c;或者通过显式类型转…
阅读更多...
Vue3使用Vite创建项目

Vue3使用Vite创建项目

node版本&#xff1a;node -v v18.16.0 npm版本: npm -v 9.5.1 Vite Vite&#xff1a;是一种新型前端构建工具&#xff0c;能够显著提升前端开发体验 脚手架&#xff0c;创建Vue项目&#xff0c;替代 Vue-cli 基于Vite创建vue项目&#xff1a; 1.npm create vitelatest 2.完…
阅读更多...
只要封装相同，电容体本身大小就一样吗？

只要封装相同，电容体本身大小就一样吗？

高速先生成员--黄刚 当然这篇文章也还是针对高速信号的交流耦合电容&#xff0c;并不是用于电源的去耦电容&#xff0c;同时文章的灵感也来源于上一篇文章讲不同容值电容对高速信号原理上的效果差异。为什么我们在做高速设计的时候&#xff0c;速率越高&#xff0c;希望电容封装…
阅读更多...
硬件小白，如何在有限的预算里选择一款性价比最高的硬盘？

硬件小白，如何在有限的预算里选择一款性价比最高的硬盘？

硬件小白&#xff0c;如何在有限的预算里选择一款性价比较高的硬盘 明确使用场景三大种类SSD、HHD、HDDSSD 固态硬盘&#xff08;Solid State Drive&#xff09;HHD 混合硬盘&#xff08;Hybrid Hard Drive)HDD 传统硬盘&#xff08;Hard Disk Drive&#xff09;小结 重要参数机…
阅读更多...
3分钟了解 egg.js

3分钟了解 egg.js

Eggjs是什么&#xff1f; Eggjs是一个基于Koajs的框架&#xff0c;所以它应当属于框架之上的框架&#xff0c;它继承了Koajs的高性能优点&#xff0c;同时又加入了一些约束与开发规范&#xff0c;来规避Koajs框架本身的开发自由度太高的问题。 Koajs是一个nodejs中比较基层的…
阅读更多...
MFC-列表控件

MFC-列表控件

目录 1、更改列表控件的属性&#xff1a; 2、代码设置表头&#xff1a; 3、设置正文内容&#xff1a; 4、设置属性&#xff0c;显示成表格形式 &#xff1a; 5、代码实现&#xff1a; 1、更改列表控件的属性&#xff1a; VIEW设置为Report模式会出现表格形状 2、代码设置…
阅读更多...
C++对象模型（14）-- 构造函数语义学：拷贝构造函数和赋值运算赋

C++对象模型（14）-- 构造函数语义学：拷贝构造函数和赋值运算赋

1、拷贝构造函数 1.1 什么是拷贝构造函数 拷贝构造函数是一种构造函数&#xff0c;它的功能是创建新对象。也就是说对象还没生成&#xff0c;这时利用另一个对象的拷贝来生成新的对象。 class MyDemo { public:// 默认构造函数MyDemo(){}// 拷贝构造函数MyDemo(const MyDemo…
阅读更多...
【Java 进阶篇】JavaScript DOM Document对象详解

【Java 进阶篇】JavaScript DOM Document对象详解

在前端开发中&#xff0c;DOM&#xff08;文档对象模型&#xff09;扮演着重要的角色。它允许我们使用JavaScript来与网页文档进行交互&#xff0c;实现动态的网页效果。DOM的核心部分之一就是Document对象&#xff0c;它代表了整个HTML文档。在本篇博客中&#xff0c;我们将深…
阅读更多...
A1S65B-S1 A1S61PN A1SJ51T64 机器人的优点和缺点

A1S65B-S1 A1S61PN A1SJ51T64 机器人的优点和缺点

A1S65B-S1 A1S61PN A1SJ51T64 机器人的优点和缺点 像今天的任何创新一样&#xff0c;机器人有其优缺点。以下是机器人的优缺点和机器人未来的分析。 优势 他们在危险的环境中工作:当你可以派一个机器人去做这项工作时&#xff0c;为什么要拿人命冒险呢&#xff1f;想想看&a…
阅读更多...
电平转换器IC

电平转换器IC

一、前言 使用多款电平转换器&#xff0c;记录和分享使用心得 目录 1.TXB0104(非国产) 2.RS0104(国产) 二、环境 非隔离电平转换&#xff0c;1.8~5V 三、正文 1.TXB0104(非国产) 芯片简介&#xff1a;A 端口支持 1.2V 至 3.6V 的电压&#xff0c;B 端口支持 1.65V 至 5…
阅读更多...
法国数字医疗公司Tilak Healthcare完成1000万欧元融资

法国数字医疗公司Tilak Healthcare完成1000万欧元融资

来源&#xff1a;猛兽财经 作者&#xff1a;猛兽财经 猛兽财经获悉&#xff0c;总部位于法国巴黎的治疗眼科的数字医疗公司Tilak Healthcare今日宣布已完成1000万欧元融资。 本轮融资完成后&#xff0c;Tilak Healthcare的融资总额已达到2200万欧元&#xff0c;本轮融资由Elai…
阅读更多...
【软件测试】高频常问自动化测试面试题+答案（汇总）

【软件测试】高频常问自动化测试面试题+答案（汇总）

目录&#xff1a;导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结&#xff08;尾部小惊喜&#xff09; 前言 1、你有没有做过自…
阅读更多...
linux文件权限与目录配置

linux文件权限与目录配置

用户与用户组 linux一般将文件可读写的身份分为三个类别&#xff1a;拥有者&#xff08;owner&#xff09;、所属群组&#xff08;group&#xff09;、其他人&#xff08;other&#xff09; 三种身份都有读、写、执行等权限 文件拥有者 linux是个多人多任务的系统&#xff0c…
阅读更多...
Edge侧实用【AI插件合集】

Edge侧实用【AI插件合集】

废话不多说&#xff0c;直接开始正文&#x1f447; 1.ChatsNow ChatsNow是人工智能助手&#xff0c;支持GPT-3.5 和 GPT-4 模型&#xff0c;写作&#xff0c;AI绘画统统不在话下&#xff0c;并且可以增强搜索引擎结果等。 免费使用&#xff0c;提供30次问答次数&#xff0c;…
阅读更多...
智慧公厕：打造清新无臭的舒适空间

智慧公厕：打造清新无臭的舒适空间

近年来&#xff0c;智慧公厕成为城市建设中备受关注的一个热点话题。而对于公共厕所最让人头痛的臭味问题&#xff0c;一直困扰着管理单位。为了解决公厕臭味问题&#xff0c;科技力量发挥了重要作用&#xff0c;中期科技「智慧公厕-智慧厕所」推出了一系列公厕除臭设备&#x…
阅读更多...
JDBC整合C3P0,DBCP,DRUID数据库连接池

JDBC整合C3P0,DBCP,DRUID数据库连接池

在使用JDBC整合数据库连接操作时,如果需要用到事务,在去关闭Connection conn的时候 注意在关闭前 注意:最好这么做一下 避免下次别人用的时候也自动开启事务,但是自己测试C3P0时候,连接池会自动将状态更新,也就是说,即使关闭前不设置为true,默认连接池也会将状态更新, 这里…
阅读更多...
基于饥饿游戏优化的BP神经网络（分类应用） - 附代码

基于饥饿游戏优化的BP神经网络（分类应用） - 附代码

基于饥饿游戏优化的BP神经网络&#xff08;分类应用&#xff09; - 附代码 文章目录 基于饥饿游戏优化的BP神经网络&#xff08;分类应用&#xff09; - 附代码1.鸢尾花iris数据介绍2.数据集整理3.饥饿游戏优化BP神经网络3.1 BP神经网络参数设置3.2 饥饿游戏算法应用 4.测试结果…
阅读更多...
win10系统防火墙 拦截未知程序，怎么在防火墙上放行？

win10系统防火墙 拦截未知程序，怎么在防火墙上放行？

如果您想让防火墙不拦截某些程序&#xff0c;可以按照以下步骤进行操作&#xff1a; 打开控制面板&#xff0c;选择系统和安全&#xff0c;点击Windows Defender防火墙&#xff1a;“Windows Defender防火墙”&#xff0c;打开防火墙设置。 点击“允许应用或功能通过“Windows…
阅读更多...
【Java学习之道】数据库的基本概念与分类

【Java学习之道】数据库的基本概念与分类

引言 在这一章中&#xff0c;我们将一起探讨数据库编程的基础知识和核心技能。作为Java程序员&#xff0c;掌握数据库编程是非常重要的&#xff0c;因为在实际开发过程中&#xff0c;我们经常需要处理大量的数据。通过本章节的学习&#xff0c;你将能够理解数据库的基本概念、…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023