原题链接：

367. 有效的完全平方数

https://leetcode.cn/problems/valid-perfect-square/submissions/

完成情况：

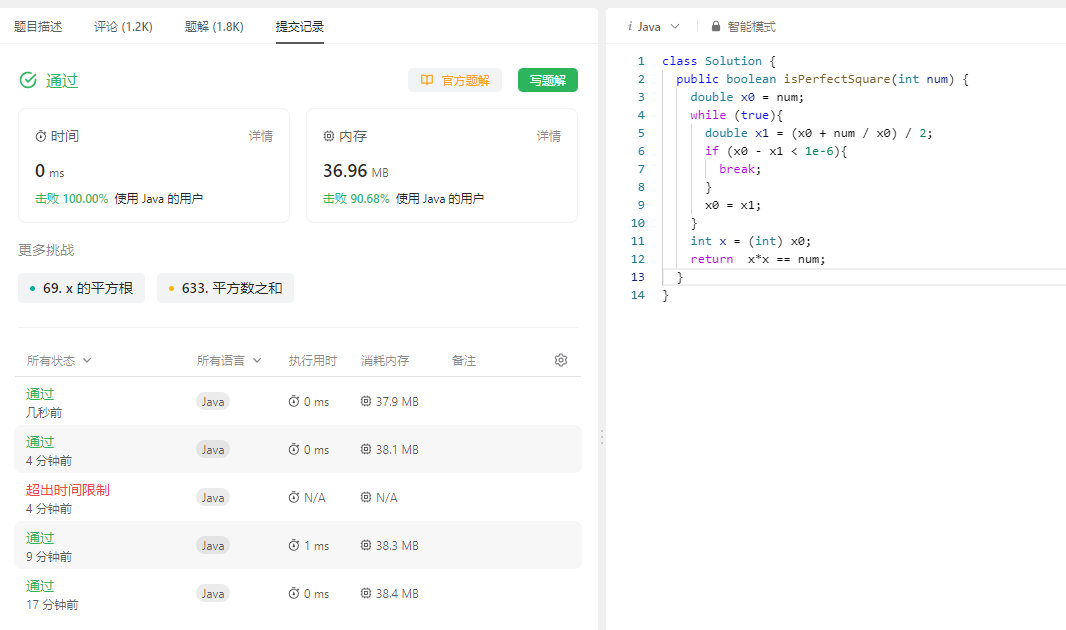
解题思路：

1. 二分查找
2. 使用内置的库函数
3. 暴力遍历
4. 牛顿迭代

参考代码：

1. 二分查找

package 日常Java程序测试.代码随想录.数组;

public class __367有效的完全平方数__二分查找 {
	/**
	 *
	 * @param num
	 * @return
	 */
	public boolean isPerfectSquare(int num) {
		int left = 0,right = num;
		while (left <= right){
			int mid = (right - left) /2 + left;
			long square = (long)mid * mid;
			if (square < num){
				left = mid + 1;
			} else if (square > num) {
				right = mid - 1;
			}else {
				return true;
			}
		}
		return false;
	}
}

2. 使用内置的库函数

package 日常Java程序测试.代码随想录.数组;

public class __367有效的完全平方数__使用内置的库函数 {
	/**
	 *
	 * @param num
	 * @return
	 */
	public boolean isPerfectSquare(int num) {
		//判断一个数是不是整数的平方
		int x = (int)Math.sqrt(num);
		return x*x == num;
	}
}

3. 暴力遍历

package 日常Java程序测试.代码随想录.数组;

public class __367有效的完全平方数__暴力遍历 {
	/**
	 *
	 * @param num
	 * @return
	 */
	public boolean isPerfectSquare(int num) {
		long x = 1,square = 1;
		while (square <= num){
			if (square == num){
				return true;
			}
			++x;
			square = x*x;
		}
		return false;
	}
}

4. 牛顿迭代

package 日常Java程序测试.代码随想录.数组;

public class __367有效的完全平方数__牛顿迭代 {
	/**
	 *
	 * @param num
	 * @return
	 */
	public boolean isPerfectSquare(int num) {
		double x0 = num;
		while (true){
			double x1 = (x0 + num / x0) / 2;
			if (x0 - x1 < 1e-6){
				break;
			}
			x0 = x1;
		}
		int x = (int) x0;
		return  x*x == num;
	}
}