https://vjudge.net/contest/587311#problem/H

先转化一波条件：

• $p_i\ge \frac{1}{X}$
• $p_i\le \frac{1}{1-Y}$

所以我们按 $p$ 排序，$su{m}_x$ 必然是后缀，$su{m}_y$ 必然是前缀。

同时发现在 $X$ 变大，$su{m}_x$ 必然变大。$Y$ 同理。

观察式子：

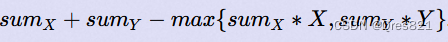
假设 $su{m}_y$ 定，且 $ma{x}_y\ast Y\ge su{m}_x\ast X$，则显然在满足条件下 $X$ 越大越好。

然后就可以two-pointers了。

要去重，不然过不了 脑抽出题人卡精度

#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;
ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+
(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//#define M
//#define mo
#define N 1000010
struct node {
	double p, c; 
}a[N];
int n, m, i, j, k, T;
double ans, S1[N], S2[N]; 
double x, y; 
int l, r; 

double calc_X(double p) {
	if(p==0) return -1; 
	return 1.0/p; 
}

double calc_Y(double p) {
	if(p==1) return -1; 
	return 1.0/(1-p); 
}

signed main()
{
//	freopen("in.txt", "r", stdin);
//	freopen("out.txt", "w", stdout);
//	srand(time(NULL));
//	T=read();
//	while(T--) {
//
//	}
	n=read(); 
	for(i=1; i<=n; ++i) scanf("%lf%lf", &a[i].p, &a[i].c); 
	sort(a+1, a+n+1, [] (node x, node y) { return x.p < y.p; }); 
	a[n+1].p=1; 
	for(i=1, j=0; i<=n+1; ++i) {
		if(a[i].p!=a[j].p) a[++j]=a[i]; 
		else a[j].c+=a[i].c; 
	} 
	n=j; 
	S1[0]=a[0].c; 
	for(i=1; i<=n; ++i) S1[i]=S1[i-1]+a[i].c; 
	for(i=n; i>=0; --i) S2[i]=S2[i+1]+a[i].c; 
//	for(i=0; i<=n; ++i) printf("%lf %lf\n", a[i].p, a[i].c); 
//	for(i=0; i<=n; ++i) printf("%lf ", S1[i]); printf("\n"); 
//	for(i=0; i<=n; ++i) printf("%lf ", S2[i]); printf("\n"); 
	for(l=0, r=n; l<=n; ++l) {
		y=calc_Y(a[l].p); if(y<0) break; 
		while(calc_X(a[r-1].p)>=0 && S2[r-1]*calc_X(a[r-1].p)<=S1[l]*y) --r; 
		for(i=min(n, r+10); i>=max(1ll, r-10); --i) {
			x=calc_X(a[i].p); if(x<0) continue; 
			if(i<=l) continue; 
//			printf("%lld %lld (%lf %lf)[%lf %lf] %lf\n", l, i, y, x, S1[l], S2[i], max(S1[l]*y, S2[i]*x)); 
			ans=max(ans, S1[l]+S2[i]-max(S1[l]*y, S2[i]*x)); 
		}
	}
	printf("%.11lf", ans); 
	return 0;
}